PUISSANCE ET ÉNERGIE EN ÉLECTRICITÉ

PUISSANCE ET ÉNERGIE EN ÉLECTRICITÉ
INTRODUCTION
Dans un circuit électrique, le récepteur reçoit de l’énergie du générateur ; lorsque le récepteur transforme cette
énergie ( en chaleur ou en énergie mécanique ) on dit qu’il consomme de la puissance . De façon plus précise, la
puissance représente la capacité du récepteur à transformer plus ou moins rapidement l’énergie qu’il reçoit.
L’unité de cette grandeur physique est le watt ( W ). Pour mesurer la puissance en électricité, on utilise un
wattmètre ou une pince multifonction .
MESURE DE PUISSANCE
Question 1 :
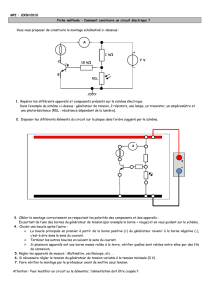
Le montage ci-dessous permet de mesurer la puissance que la source fournit à une résistance.
La pince MX 240 mesure la tension V , l’intensité du courant , I et la puissance P. Le récepteur est un rhéostat de
100 Ω . Le générateur est une alimentation continue AX 503.
V
I
R
v
PM
G
FAIRE VERIFIER
Question 2 :
Mettre sous tension et régler la tension à 24 V. Régler R pour que I = 2 A Relever la valeur de P donnée par la
pince.
Question 3 :
A partir des valeurs de P , I et V établir la relation qui permet de calculer P en fonction de V et I.
Question 4 :
Débrancher le rhéostat et mesurer sa valeur ; à partir des valeurs de P , I et R établir la relation qui permet de
calculer la puissance consommée par une résistance en fonction de R et I.
Question 5 :
La résistance consomme de la puissance : elle transforme donc l’énergie électrique qu’elle reçoit . Sous quelle
forme ?
INFLUENCE DE LA LIGNE DE TRANSPORT
En général, le générateur et le récepteur sont éloignés l’un de l’autre : pour transporter l’énergie, on utilise des fils
de grande longueur ( la ligne ). Dans l’étude suivante, on simulera une ligne de transport avec un « rouleau » de
fil de 200 m de longueur.

Question 6 :
Réaliser le montage ci-dessous.
V
I
R
v
PM
G
rouleau de fil
FAIRE VERIFIER
Question 7 :
Mettre sous tension et régler V à 24 V ; régler R pour avoir I = 2 A . Relever la puissance P
G
fournie par le
générateur.
Question 8 :
Après avoir mis le montage hors tension, déplacer la pince pour mesurer la puissance P
R
consommée par la
résistance.
Question 9 :
Comparer P
G
et P
R
; comment expliquer la différence ?
Question 10 :
Calculer la puissance « perdue » dans la ligne et l’exprimer en pourcentage de la puissance fournie par le
générateur.
Question 11 :
En déduire la résistance R
L
de la « ligne ».
INFLUENCE DE LA TENSION
Question 12 :
Reprendre le montage de la question 6 : régler V à 48 V ( pour obtenir cette valeur, il faudra mettre les deux
sources de l’alimentation en série et les régler à 24 V ) ; ensuite, régler le rhéostat pour que la puissance fournie
par le générateur soit la même que celle de la question 7.
FAIRE VERIFIER
Question 13 :
Déplacer la pince pour mesurer P
R
. Calculer la puissance perdue dans la ligne et l’exprimer en pourcentage de la
puissance fournie par le générateur . Faire une conclusion et justifier l’existence des lignes à haute tension pour le
transport de l’énergie électrique.

RESISTANCE D’UN FIL
Pour calculer la résistance d’un fil on utilise la relation ci-dessous:
R =
slρ
ρρ
ρ
l désigne la longueur du fil en m
s la section en m²
ρ
ρρ
ρ ( ça se dit « ro » ) est appelée « résistivité » du matériau qui constitue le fil ( unité : Ω
ΩΩ
Ω.m ) Plus la
résistivité est faible et plus le matériau est bon conducteur.
On donne ci-dessous la résistivité de quelques matériaux courants :
Argent : ρ
ρρ
ρ = 1,5 × 10
-8
Ω
ΩΩ
Ω.m
Cuivre : ρ
ρρ
ρ = 1,6 × 10
-8
Ω
ΩΩ
Ω.m
Aluminium : ρ
ρρ
ρ = 2,6 × 10
-8
Ω
ΩΩ
Ω.m
Tungstène : ρ
ρρ
ρ = 5 × 10
-8
Ω
ΩΩ
Ω.m
Fer : ρ
ρρ
ρ = 8,5 × 10
-8
Ω
ΩΩ
Ω.m
Question 14 :
Retrouver, à l’aide de la relation ci-dessus, la valeur de la résistance R
L
du rouleau de fil ( celle que vous avez
calculée à la question 11 ) sachant qu’il est en cuivre et que la section est de 1,5 mm² .
Question 15 :
La résistance des fils a t-elle une influence lorsqu’on réalise des montages « traditionnels » ? Pour répondre à
cette question, calculer la résistance d’un fil de câblage en cuivre utilisé au laboratoire : longueur 1 m , section
1,5 mm².
LA RESISTIVITE D’UN MATERIAU DEPEND DE LA TEMPERATURE
La résistivité des métaux et des alliages est fonction de la température : les valeurs ρ
ρρ
ρ
0
et ρ
ρρ
ρ
θ
θθ
θ
de la résistivité
respectivement à 0°C et à θ
θθ
θ°C sont liées par la relation :
ρ
ρρ
ρ
θ
θθ
θ
= ρ
ρρ
ρ
0
(1+ a.θ
θθ
θ)
Dans laquelle a est appelé « coefficient de température » ; pour les métaux, a = 4×10
-3
°C
-1
Comme la résistance est proportionnelle à la résistivité, on peut écrire :
R
θ
θθ
θ
= R
0
(1+ a.θ
θθ
θ)
Question 16 :
Résoudre l’ exercice :
Une lampe à incandescence est alimentée sous 240 V . Quelques minutes après la mise sous tension, la
température du filament atteint 2500 °C et elle consomme alors une puissance de 75 W.
1) Calculer à cette température l’intensité i
N
du courant qui la traverse et la valeur R
N
de la résistance de son
filament.
2) Au moment de la mise sous tension, la température est T
0
= 20 °C. Calculer à cette température la
résistance R
A
de son filament et l’intensité i
A
du courant.
Le coefficient de température est a = 4×
××
×10
-3
°C
-1
.
3) Déterminer la valeur du rapport
A
N
i
i.