A savoir

LES QUADRILATERES
I. Le quadrilatère quelconque
A savoir
Un quadrilatère est une figure géométrique ayant quatre côtés.
Vocabulaire
A, B, C et D sont les sommets du quadrilatère ci-dessus.
Pour nommer ce quadrilatère, il suffit de les citer dans l’ordre où ils apparaissent en
parcourant le quadrilatère.
Différents noms possibles : ABCD, BCDA, DCBA, … mais pas ABDC.
diagonales
côtés opposés
côtés consécutifs
A
D
C
B
angles opposés

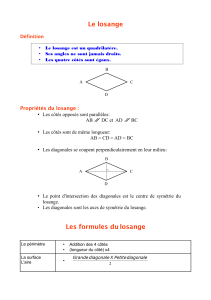
II. Le losange
1. Définition
A savoir
Un losange est un quadrilatère qui a 4 côtés de la même longueur.
2. Propriétés
Axes de symétries
A savoir : Un losange a 2 axes de symétrie : ses diagonales.
Diagonales d’un losange
A savoir
Les diagonales d’un losange sont perpendiculaires et ont le même milieu.

3. Constructions à savoir faire
a) Construire un losange connaissant la longueur de ses côtés
Exemple 1 : Construire un losange ABCD tel que AB = 4 cm.
Programme de construction
 On trace des segments [AB] et [AD] de longueur 4 cm.
 On trace des arcs de cercle de centres B et D et de
rayon 4 cm.
 On nomme C leur point d’intersection.
 On trace [CB] et [CD].
Il y a plusieurs figures possibles
b) Construire un losange connaissant la longueur de ses diagonales
Exemple 2 : Construire un losange VERT tel que VR = 3 cm et ET = 5 cm.
Programme de construction
 On trace un segment [VR] de longueur 3 cm.
 On trace le segment [ET] de longueur 5 cm, passant
par le milieu de [VR] et perpendiculaire à [VR].
 On relie V, E, R et T.
c) Construire un losange connaissant un côté et une diagonale
Exemple 3 : Construire un losange ANGE tel que AN = 3,3 cm et AG = 5,2 cm.
Programme de construction
 On trace un segment [AG] de longueur 5,2 cm.
 On trace deux arcs de cercle de centres A et de rayon
3,3 cm.
 On trace deux arcs de cercle de centres G et de rayon
3,3 cm.
 On nomme N et E leurs points d’intersection.
 On relie A, N, G et E.

III. Le rectangle
1. Définition
A savoir
Un rectangle est un quadrilatère qui a 4 angles droits.
2. Propriétés
Axes de symétries
A savoir
Un rectangle a 2 axes de symétrie : les médiatrices des côtés opposés.
Diagonales d’un rectangle
A savoir
Les diagonales d’un rectangle ont le même milieu et la même longueur

3. Constructions à savoir faire
a) Construire un rectangle connaissant sa longueur et sa largeur
Exemple : Construire un rectangle ABCD de 5 cm de longueur et de 3 cm de largeur.
Programme de construction
 Tracer un segment [AB] de longueur 5 cm.
 Tracer une demi-droite d’origine A et perpendiculaire à [AB]
 Placer sur cette demi-droite le point D tel que AD = 3 cm.
 Faire de même à partir du point B, nommer C le point obtenu.
 Tracer le segment [CD].
b) Construction d’un rectangle connaissant la longueur d’une des diagonales
Exemple : Construire un rectangle dont une diagonale mesure 5 cm :
Les diagonales se coupent en leur milieu et ont la même longueur
Programme de construction :
 Tracer deux segments de longueur 5 cm et ayant le même milieu
 Relier les 4 extrémités.