Activité documentaire et expérimentale N°1 (P6) 1°) Décrire

Activité documentaire et expérimentale N°1 (P6)
1°) Décrire simplement le mouvement d’un sportif :
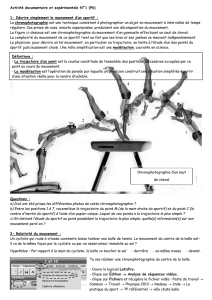
La chronophotographie est une technique consistant à photographier un objet en mouvement à intervalles de temps
réguliers. Ces prises de vues, ensuite superposées, produisent une décomposition du mouvement.
La figure ci-dessous est une chronophotographie du mouvement d’un gymnaste effectuant un saut de cheval.
La complexité du mouvement de ce sportif tient au fait que ses bras et ses jambes se meuvent indépendamment.
Le physicien, pour décrire un tel mouvement, en particulier sa trajectoire, se limite à l’étude d’un des points du
sportif judicieusement choisi. Une telle simplification est une modélisation, courante en science.
Questions :
a) D’où ont été prises les différentes photos de cette chronophotographie ?
b) Entre les positions 1 à 7, reconstitue la trajectoire du point M (de la main droite du sportif) et du point C (le
centre d’inertie du sportif) à l’aide d’un papier calque. Lequel de ces points a la trajectoire la plus simple ?
c) En limitant l’étude du sportif au point possédant la trajectoire la plus simple, quelle(s) information(s) sur son
mouvement perd-on ?
2°) Relativité du mouvement :
Chronophotographie d’un saut
de cheval
C
M
1
2
3
4
5
6
7
+
+
Définitions :
- La trajectoire d’un point est la courbe constituée de l’ensemble des positions successives occupées par ce
point au cours du mouvement.
- La modélisation est l’opération de pensée par laquelle un physicien construit une situation simplifiée à partir
d’une situation réelle pour la rendre étudiable.
Un motard qui roule à vitesse constante laisse tomber une balle de
tennis (sans la lancer).
Le mouvement du centre de la balle est-il vu de la même façon par
le motard et par un observateur immobile par rapport au sol ?
Tu vas réaliser une chronophotographie du centre de la balle.
- Ouvre le logiciel Synchronie 2006.
- Puis dans Synchronie, clique sur Édition  Image ou séquence
vidéo  Pointage de mobile.
- Récupère le fichier vidéo : Poste de travail  Commun 
Travail  Sciences Physiques  Nadeau  2nde  mécanique
2nde  moto chute balle.avi.
1
2

Questions :
a) Représente les deux trajectoires obtenues sur ton cahier. Quel outil géométrique utilise-t-on pour repérer la
position d’un point sur un objet ?
b) Des deux trajectoires représentées, quelle est celle qui est vue par le motard ? Quelle est la nature de cette
trajectoire ? Justifie en comparant la position de la main et celle de la balle (clique sur Édition  Image ou
séquence vidéo  Pointage de mobile pour visualiser à nouveau la vidéo).
c) Des deux trajectoires représentées, quelle est celle qui est vue par un observateur immobile par rapport au sol ?
Quelle est la nature de cette trajectoire ? Justifie.
d) On appelle référentiel le solide de référence muni d’un repère spatial et d’une horloge par rapport auquel
on décrit le mouvement d’un objet. Quels sont les deux référentiels utilisés ici ?
e) La forme de la trajectoire dépend-elle du référentiel choisi pour étudier le mouvement ?
f) Compare les distances parcourues entre les deux dernières images par la balle dans chacun des référentiels. Que
constates-tu ?
Conclusion : Que faut-il obligatoirement préciser quand on étudie le mouvement d’un point d’un objet ?
3°) Utilisation de la chronophotographie : trouver d’autres chronophotographies
On étudie les trois chronophotographies suivantes par rapport au référentiel terrestre :
(a) Balle de golf
(b) Ballon de foot
(c) Pierre de curling
Questions :
Pour chaque chronophotographie, réponds aux questions suivantes :
a) Indique si la trajectoire du point est rectiligne, circulaire ou curviligne (courbe quelconque).
b) Sans calcul, comment évolue la vitesse du point au cours du temps ? Justifie.
c) En choisissant un mot dans chaque liste, qualifie le mouvement (trajectoire et vitesse) du point ? Justifie.
 Liste 1 : rectiligne, circulaire, curviligne.
 Liste 2 : uniforme, ralenti, accéléré.
d) Chronophotographie de la balle de golf : l’intervalle de temps entre chaque photo est de 80,0 ms et l’échelle
utilisée est : 1,0 cm sur le schéma représente 20,0 cm dans la réalité.
- Calcule la vitesse moyenne (en m∙s–1) du point entre les positions 1 et 6. Convertis-la en km∙h-1.
- Calcule la vitesse moyenne (en m∙s–1) du point entre les positions 2 et 4. Compare-la à celle calculées au a).
- Compare ces deux vitesses moyennes. Sont-elles égales à la vitesse instantanée ? Justifie.
e) Chronophotographie de la pierre de curling : l’intervalle de temps entre chaque photo est de 180,0 ms et l’échelle
utilisée est : 1,0 cm sur le schéma représente 40,0 cm dans la réalité.
- Calcule la vitesse moyenne (en m∙s–1) du centre d’inertie de la pierre entre les positions 1 et 5.
- De la même façon, calcule la vitesse moyenne (en m∙s–1) du même point entre les positions 3 et 5. Compare-
la à celle calculées au a).
- A ton avis, quelle est la vitesse moyenne (parmi les deux calculées précédemment) la plus proche de la
vitesse instantanée du point en position 4 ? Justifie.
- Clique sur Origine : le bas de la roue avant en contact
avec le sol.
- Clique sur Étalonnage : fixe la distance avec l’étalon
indiqué à L = 0.6 m (clique sur le bas de l’étalon et glisse la
souris jusqu’en haut de l’étalon en maintenant appuyé).
- Coche Mouvement relatif  Clique sur Pointeur 
Choisis la forme du pointeur  Avance la vidéo à l’image
N°11, soit 400 ms  Pointe d’abord l’objet de référence
(le rétroviseur), puis la position du centre de la balle (à
chaque pointage, la vidéo avance à l’image suivante). Fais
les pointages jusqu’à l’image N°24, soit 920 ms.
- Clique sur Pointeur  Exporter  Coche Yi = f(Xi)
(repère absolu) et Yi = f(Xi) (repère relatif).
- Fenêtre n°1 : Yi =f(Xi) (repère absolu).
- Fenêtre N°2 : Yi = f(Xi) (repère relatif).
1
2
3
4
3
3