Document

Hydromécanique HZS-OE5-GN240 - C. Reynaerts
Version 7.0 Décembre 2011
2-1
2 Les forces hydrostatiques
Dans ce chapitre tu apprends,
 à calculer la force résultante suite à la pression hydrostatique sur une paroi
plane,
 à déterminer la position du centre de pression (NL drukpunt ou perspunt), le
point d’action de la force résultante suite à la pression hydrostatique, sur une
paroi plane
 à calculer la force résultante suite à la pression hydrostatique sur une paroi
courbée au plan de symétrie vertical,
 à appliquer la loi d’Archimède.

Hydromécanique HZS-OE5-GN240 - C. Reynaerts
Version 7.0 Décembre 2011
2-2
2.1 La force résultante suite à la pression hydrostatique sur une
paroi plane
2.1.1 La force résultante
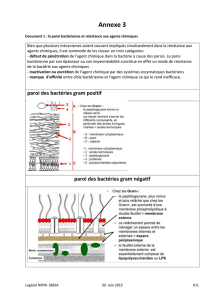
Considérez un liquide à densité  qui se trouve dans un récipient avec une paroi
latérale plane sous un angle  avec l’horizontale. Le graphique ci-dessous montre
une section dans un plan vertical. Dans la paroi latérale plane nous définissons un
système de repère dont l’axe x coïncide avec la ligne d’intersection de la paroi
latérale plane et de la surface du liquide. La position de l’axe y est indiquée dans le
graphique ci-dessous. Il y a un rapport simple entre la coordonnée y et la profondeur
h en dessous de la surface du liquide
yh sin
ou
h y  sin
.
Le graphique ci-dessus montre la position du centre de gravité (NL zwaartepunt)
d’une surface qui fait partie de la paroi latérale. La position du centre de pression (NL
drukpunt ou perspunt), comme on appelle le point d’action de la force résultante suite
à la pression hydrostatique sur cette surface est également indiquée.
Considérez une fraction élémentaire dxdy de cette surface dans la paroi. Elle se
trouve à une profondeur h au-dessous de la surface du liquide.
Il y a 2 forces qui agissent perpendiculairement sur cet élément,
 une force dirigée vers l’extérieur, avec une intensité
(p )
og h dx dy    
, ou po est
la pression à la surface du liquide,
 une force dirigée vers l’intérieur, avec une intensité
pdx dy
o 
.
0
hz = hcg
yz = ycg
hP = hD = hcp
yP = yD = ycp
y
dy
dx
A
(p )
og h dx dy    
pdx dy
o 

Hydromécanique HZS-OE5-GN240 - C. Reynaerts
Version 7.0 Décembre 2011
2-3
Forcément, la force nette sur l’élément est également perpendiculaire à la paroi. Elle
est dirigée vers l’extérieur et son intensité est égale à
   g h dx dy
.
En conséquence, la force résultante sur la surface dans la paroi est également
perpendiculaire à la paroi latérale. Elle est dirigée vers l’extérieur et son intensité est
égale à
Ahg
AsinygyAsing
A
dydxy
Asing
dydxysingdydxsinygdydxhgF
cg
cgcg
A
AAA
R
ou A est la superficie de la surface considérée. Autrement dit, la pression
hydrostatique à la profondeur du centre de gravité de la surface dans la paroi,
multipliée par sa superficie A.
2.1.2 Le centre de pression
La force résultante sur une surface dans la paroi latérale a la même intensité qu’elle
aurait dans le cas d’une pression uniforme, égale à la pression à profondeur du
centre de gravité. Dans le cas d’une pression uniforme la force résultante agirait au
centre de gravité de la partie. En réalité, la pression est plus petite dans les points
moins profonds que le centre de gravité, et plus élevée dans les points plus profonds.
En conséquence, le point d’action de la force résultante se trouve à une profondeur
supérieure à celle du centre de gravité. La position du centre de pression est obtenue
par l’application du théorème des moments de Varignon, “le moment de la résultante
= moment résultant”.
L’intensité du moment de la force résultante par rapport au point 0 est égale à
AsinygyFy cgpRp 
.
Vu que la force résultante est perpendiculaire à la paroi, son bras de force par
rapport à 0 n’est rien d’autre que la coordonnée y du centre de pression, yp.
D’une façon similaire l’intensité du moment de force élémentaire de la force nette sur
une surface élémentaire dxdy est égale à
y g y dx dy      sin
.
Alors, l’intensité du moment résultant est égale à
y g y dx dy g y dx dy g I
A A x
sin sin sin
2
ou Ix est le moment d’inertie de la surface par rapport à l’axe x (une ligne horizontale
à l’intersection de la surface du liquide et de la paroi). L’application du théorème de
Steiner pour les axes parallèles donne le résultat suivant

Hydromécanique HZS-OE5-GN240 - C. Reynaerts
Version 7.0 Décembre 2011
2-4
)AyI(singIsing 2
cgxx 
ou
Ix
est le moment d’inertie de la surface par rapport à un axe parallèle à l’axe x et
passant par le centre de gravité de la surface A.
En conséquence,
)AyI(singAsinygy 2
cgxcgp
et
Ay I
yy
Ay I Asinyg )AyI(sing
ycg
x
cgcg
cg
x
cg
2
cgx
p
ce qui prouve formellement que le centre de pression se trouve plus profondément
que le centre de gravité de la surface A.
2.2 La force résultante suite à la pression hydrostatique sur une
paroi courbée au plan de symétrie vertical
En général, calculer la force résultante suite à la pression hydrostatique sur une paroi
courbée n’est pas évident. On va se limiter au cas d’une paroi au plan de symétrie
vertical. Dans ce cas on est assuré que la force résultante se trouve dans ce plan.
Considérez un liquide limité par une telle paroi courbée et éventuellement en partie
par une paroi plane verticale. Le graphique ci-dessous montre une section dans le
plan de symétrie vertical van de la paroi courbée.
Considérez un plan vertical passant par le point B, le point au pied de la paroi
courbée. Dans la section elle est représentée par la ligne DB. Le point C sur la ligne
DB se trouve à la même profondeur que le point A. Considérons l’équilibre statique
du liquide limité d’un coté par la paroi plane EA et la paroi courbée AB et de l’autre
coté par les parois planes (hypothétiques) DC et CB. Les forces suivantes agissent
sur ce liquide
E
A
B
D
C
FDC
FEA
FG
FCB
Fh
Fv

Hydromécanique HZS-OE5-GN240 - C. Reynaerts
Version 7.0 Décembre 2011
2-5
 la force de réaction
FEA
de la paroi plane EA suite à la force hydrostatique
résultante sur EA, agissante dans le centre de pression associé;
 la force hydrostatique résultante
FDC
sur DC, agissante dans le centre de pression
associé;
 la force de réaction
FAB
de la paroi courbée AB suite à la force hydrostatique
résultante sur AB;
 la force hydrostatique résultante
FCB
sur CB, agissante dans le centre de pression
associé;
 le poids
FG
du liquide, agissant dans le centre de gravité.
La force
FAB
est perpendiculaire à la paroi courbée. En conséquence, elle est
parallèle à la normale à la courbe AB dans son point d’action. Autrement dit, sa ligne
d’action passe par le centre de courbure de la courbe AB à ce point. Décomposons
FAB
en une composante horizontale et une composante verticale
F F F
AB h v
.
L’équilibre du liquide exige que la force résultante soit nulle. Exprimé en termes des
intensités des forces cela dit que
F F
F F F F
G v
EA hDC CB
.
Vu la symétrie,
F F
EA DC
et ainsi la deuxième expression se simplifie comme suit
F F
hCB
.
La composante verticale de la force résultante suite à la pression hydrostatique sur
une paroi courbée est égale au poids du liquide se trouvant au-dessus de la paroi
courbée.
1
La composante horizontale de la force résultante suite à la pression hydrostatique
sur une paroi courbée est égale à la force résultante hydrostatique sur la projection
verticale de la paroi courbée.
2
L’équilibre du liquide exige également que le moment résultant soit nul. En
conséquence, il faut d’un coté que les lignes d’actions de Fv et de FG soient les
mêmes, autrement dit, que la ligne d’action de Fv passe par le centre de gravité du
liquide considéré. D’un autre coté, il faut que les lignes d’actions de Fh et de FCB
soient les mêmes, autrement dit, que la ligne d’action de Fh passe par le centre de
pression
3
de CB.
1
La pression hydrostatique dont on veut déterminer la force résultante, dépend uniquement de la
profondeur au dessous de la surface du liquide. En conséquence, le procédé s’applique également au
cas ou le liquide se trouve à l’extérieur de la paroi, du moins à condition que l’épaisseur de la paroi
soit négligeable. Dans ce cas, la composante verticale de la force résultante est égale au poids du
liquide imaginairement présent en dessous de AB.
2
Afin de déterminer cette composante, on applique le procédé pour le calcul de la force résultante sur
une paroi plane comme expliqué ci-devant dans ce chapitre.
3
Afin de le déterminer, on applique à nouveau le procédé pour une paroi plane comme expliqué ci-
devant dans ce chapitre.