1314_1S_compo_1_correction

Correction COMPO 1 – Premières S – 15 nov 2013
PARTIE 1 – Capter la lumière
1 . De quel type d’objet parle Descartes lorsqu’il mentionne les « verres brûlants ».
Descartes parle de lentilles convergentes, qui sont capables de faire converger la lumière en leur foyer
image F’. Cette concentration ponctuelle d’énergie lumineuse permet de mettre le feu à un combustible
placé dans le plan focal image de la lentille.
2 . Que représentent les verres « un peu plus épais au milieu qu’aux extrémités » et « beaucoup plus
épais aux extrémités qu’au milieu ». Qu’est-ce qui différencie ces deux « verres » ? Qu’ont-ils en
commun ?
verres « un peu plus épais au milieu qu’aux extrémités » : lentille peu convergente, de grande distance
focale (l’objectif) ;
verres « beaucoup plus épais aux extrémités qu’au milieu » : lentille très convergente, de courte
distance focale (l’oculaire)
Il s’agit dans les deux cas de lentilles convergentes….
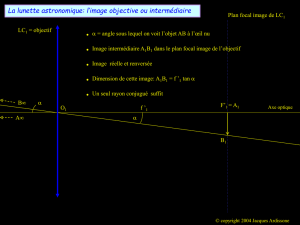
 Le diamètre apparent d’un objet est l’angle sous lequel un observateur voit l’objet.
Un observateur terrestre situé à l’observatoire de Meudon observe à l’œil nu la Lune. Il sait que le
diamètre lunaire vaut DL = 1,72.103 km et que la distance Terre-Lune est DT/L = 3,67.105 km.
3 . Montrer que le diamètre apparent de la Lune pour cet observateur est de = 0,269°.
Lune oeil
DT/L
DL
tan DL
DT/L
car petit
AN : 1,72.103.103
3,67.105.1034,69 rad 0,269 
 On considère deux points A et B de la Lune, diamétralement opposés. L’observateur braque la
grande lunette de l’observatoire dans la direction du point A.
4 . Pourquoi les faisceaux lumineux issus des points A et B et qui pénètrent dans la lunette sont
parallèles ?
La distance qui sépare les points A et B du centre optique de l’objectif de la lunette est très grande par
rapport au diamètre de l’objectif. Les cônes de lumière, issus de A et de B, lorsqu’ils pénètrent dans
l’objectif, peuvent être assimilés à des cylindres lumineux.
 Pour l’objectif L1, la Lune constitue un objet AB « à l’infini ».
5 . Où se situe l’image A1B1 de cet objet AB à travers l’objectif L1 ? Retrouver ce résultat en calculant la
distance O1A1 à l’aide de la relation de conjugaison.
L’image A1B1 de l’objet AB, situé à l’infini par rapport à l’objectif L1, se situe dans le plan focal image de
l’objectif.
On peut retrouver ce résultat à partir de la relation de conjugaison :
1
O1A1
1
O1A1 O1F'1
1
O1A1
1
O1A1 O1F'1
O1F'1O1A
O1A.O1F'1
O1A1O1A.O1F'1
O1F'1O1A

O1A O1F'1d'où :O1F'1O1AO1A
donc :O1A1O1A.O1F'1
O1F'1O1AO1A.O1F'1 O1AO1F'1
L’image A1 de A à travers l’objectif est confondue avec le foyer image F’1 de l’objectif.
6 . Compléter le schéma 1 de l’annexe en traçant l’image A1B1 de AB à travers l’objectif L1 et en
faisant figurer ainsi que A et B.
 L’observateur a réglé sa lunette de telle manière que la distance O1O2 qui sépare les centres optiques
de l’objectif et de l’oculaire vaille 16,030 m. On nomme A2B2 l’image de A1B1 à travers la lentille L2
(oculaire).
7 . Sans effectuer de calculs et en s’aidant éventuellement d’un schéma, prévoir les caractéristiques de
l’image A2B2 de A1B1 à travers l’oculaire.
Telle qu’elle est réglée, l’image A2B2 de A1B1 à travers l’oculaire va être droite et virtuelle. En effet, la
position O2A1 de A1B1 par rapport à l’oculaire est légèrement inférieure à la distance focale O2F’2 de
l’oculaire.
8 . En utilisant la relation de conjugaison, déterminer la position O2A2 de cette image.
F'1 F2
objectif oculaire
O1O2
16,030 m
16,000 m 0,040 m
échelle non respectée
1
O2A2
1
O2A1
1
O2F'2
1
O2A2
1
O2A1
1
O2F'2
O2F'2O2A1
O2A1.O2F'2
O2A2O2A1.O2F'2
O2F'2O2A1
16,030 16,000
 .0,040
0,040 16,030 16,000
    0,12 m
 Pour éviter d’avoir à accommoder, l’observateur modifie légèrement la distance O1O2 qui sépare les
deux lentilles.
9 . Après avoir rappelé le principe de l’accommodation de l’œil, dire comment l’observateur va modifier
cette distance et pour quelle raison ?
- Un œil sain ne fait aucun effort d’accommodation pour voir net un objet infiniment éloigné du cristallin.

L’image de cet objet se forme directement sur la rétine située exactement dans le plan focal image du
cristallin. Si l’objet se rapproche, son image s’éloigne vers la droite du plan focal image du cristallin.
L’image est vue floue. Pour la voir nette, l’observateur accommode afin de ramener cette image sur la
rétine. Pour cela, il contracte les muscles cillaires et comprime ainsi son cristallin afin de diminuer sa
distance focale.
- Le réglage optimal de la lunette consiste à faire coïncider le plan focal image de l’objectif et le plan
focal objet de l’oculaire. Ainsi, l’image A2B2 de A1B1 à travers l’oculaire va se situer à l’infini. En plaçant
son œil derrière l’oculaire, l’observateur va ainsi observer sans aucun effort d’accommodation l’image
de A2B2 à travers son cristallin directement sur sa rétine.
 On suppose que la lunette est réglée de telle manière que les deux lentilles L1 et L2 soient séparées
de 16,040 m.
10 . Que peut-on dire du plan focal image de L1 et du plan focal objet de L2 ? Où se situe l’image A1B1
de AB à travers l’objectif L1 ? Où se situe l’image A2B2 de A1B1 à travers l’oculaire L2 ?
- Le plan focal image de l’objectif est confondu avec le plan focal objet de l’oculaire.
- L’image A1B1 de AB à travers l’objectif se situe dans le plan focal image de l’objectif et dans le plan
focal objet de l’oculaire.
- L’image A2B2 de A1B1 à travers l’oculaire est à l’infini.
11 . Compléter le schéma 2 de l’annexe en traçant les deux faisceaux lumineux issus des points A et
B qui traversent la lunette astronomique.
 On note ’ l’angle sous lequel l’astrophysicien voit l’image A2B2 de la Lune à travers la lunette. Par
définition, le grossissement de la lunette est égal au rapport ’ / . ( Donnée : tan a a si a est petit ).
12 . Montrer que ce grossissement peut aussi s’exprimer comme étant le rapport f’1 / f’2 des distances
focales de l’objectif et de l’oculaire.
tan A1B1
O1F'1
et tan 'A1B1
O2F2
tan .f'1tan '. f'2
tan '
tan
f'1
f'2
'
car et 'sont petits
conclusion :G
'
f'1
f'2
 Grâce au grossissement d’un tel instrument, Galilée a été capable de décrire avec précision le relief
lunaire. Que se passe-t-il si l’on cherche à observer des étoiles très éloignées de la Terre de telle sorte
que leurs diamètres apparents soient pratiquement nuls ? L’observateur de ces étoiles, même à
travers une lunette très grossissante, conservera leur apparence sous forme de points lumineux car ’
demeurera très faible.
13 . Dans ce cas-là précis, quel est l’intérêt de la lunette ?

La lunette reçoit la lumière émise par les étoiles à travers son objectif de diamètre 80 cm. A l’œil nu,
l’observateur reçoit la lumière émise par les étoiles à travers son iris, d’un diamètre de quelques
millimètres. En plaçant son œil derrière l’oculaire de sa lunette, l’observateur observe donc le ciel
comme si son iris avait le même diamètre que l’objectif ! Il va donc observer beaucoup plus d’étoiles
qu’à l’œil nu… Par contre, ces étoiles seront toujours ponctuelles.
PARTIE 2 – Analyser la lumière
1 . Déterminer graphiquement la longueur d’onde
max de la radiation émise par le Soleil avec la plus
grande intensité ? Pour répondre à cette question, on superposera sur le profil spectral du Soleil
(document 4) son profil spectral général (profil spectral d’un corps noir porté à la même température).
Par lecture graphique : max = 480 nm
2 . En déduire la température de surface de l’étoile en K puis en °C .
D’après la loi de Wien :
TK
max
2,89.103
480.1096,02.103K
T273 6,02 0,273
 .1035, 75.103C
3 . Comment évolue le spectre d’émission d’un corps au fur et à mesure que sa température augmente
? Justifier en utilisant la loi de Wien.
D’après la loi de Wien, la température est inversement proportionnelle à la longueur d’onde de la
radiation émise avec le maximum d’intensité par le corps incandescent.
Plus la température augmente, plus max diminue. Le spectre s’enrichit en faibles longueurs d’onde
(bleues)
4 . Comment nomme-t-on le spectre du document 4 (spectre de Fraunhofer) ?
Il s’agit d’un spectre de raies d’émission.
5 . Quelle est l’origine du fond continu de lumière du spectre du document 4 ?
Le fond continu est un spectre continu d’émission d’origine thermique, émis par le noyau du
Soleil.
6 . Etablir un tableau donnant les valeurs des longueurs d’onde des raies repérées par les lettres B, C,
D, E, F et G du spectre du document 4.
G
F
E
D
C
B
430 nm
485 nm
530 nm
590nm
660 nm
685 nm
7 . Interpréter la présence des raies sombres B, C, D, E, F et G sur le spectre de Fraunhofer.
Les raies sombres correspondent à des raies d’absorption. Elles sont caractéristiques d’une entité
chimique présente dans l’atmosphère du Soleil qui absorbe certains photons émis par la surface de
l’étoile. Elles permettent d’identifier les éléments chimiques présents dans l’atmosphère du Soleil. En
effet, l’énergie des atomes et ions présents dans l’atmosphère du Soleil est quantifiée. Ces éléments
vont donc être capables d’absorber les photons dont l’énergie permet exactement d’effectuer des
transitions entre différents niveaux énergétiques.
G
F
E
D
C
B
430 nm
485 nm
530 nm
590nm
660 nm
685 nm
hydrogène
hydrogène
Ion potassium
sodium
hydrogène
??
 Pour analyser le spectre du Soleil, un astrophysicien utilise un spectroscope dont le prisme est en
verre S-NPH53. On considère une radiation de longueur d’onde dans le vide
0 = 587,6 nm.

8 . Que vaut l’indice de réfraction du verre S-NPH53 pour cette radiation ?
D’après le document 3, par lecture graphique, n = 1,85
9 . Calculer la vitesse de propagation de la radiation de longueur d’onde dans le vide
0 = 587,6 nm,
dans le prisme du spectroscope. (donnée : vitesse de la lumière dans le vide : c0 = 3,00.108 m.s-1)
vmilieu c0
nmilieu
3,00.108
1,85 1,62.108m.s1
10 . Calculer l’énergie du photon associé à cette radiation puis sa fréquence.
Calcul de l’énergie du photon :
Ephoton hc0
0
6,63.1034.3,00.108
587,6.1093, 38.1019 J
Calcul de la fréquence du photon :
photon c0
0
3,00.108
587,6.1095,11.1014 Hz
11 . Calculer la longueur d’onde de la radiation dans le prisme en verre S-NPH53.
La fréquence est indépendante du milieu de propagation, ce qui n’est pas le cas de la longueur d’onde.
photon c0
0
vverre
verre
c0
nverre
verre
c0
nverre.
verre
verre c0
nverre.
photon
3,00.108
1,85.5,11.1014 3,17.107m
12 . A quoi s’attendaient Kirchhoff et Bunsen lors de leur première expérience avec le spectre solaire et
le sodium ? Quel phénomène observent-ils finalement ? comment nomme-t-on le spectre observé ?
Kirchhoff et Bunsen s’attendent à ce que les doubles raies brillantes du sodium rendent plus brillantes
les raies de sodium du Soleil.
Ils observent l’inverse : des raies noires sur le fond continu du spectre de la lumière du Soleil.
Le spectre obtenu est un spectre de raies d’absorption.
13 . Chaque loi énoncée par Kirchhoff définit un type de spectre. Préciser lequel.
1ère loi : Spectre d’émission continu d’origine thermique.
2ème loi : Spectre d’émission de raies.
3ème loi : Spectre d’absorption de raies.
14 . Expliquer la phrase en justifiant : « un gaz émet et absorbe des raies de mêmes couleurs » .
La comparaison d’un spectre d’émission et d’absorption d’une même entité chimique montre que les
longueurs d’ondes des raies émises sont les mêmes que les longueurs d’ondes des raies absorbées
sur le spectre continu.
Ceci s’explique par la quantification de l’énergie de l’atome. L’énergie des photons absorbés ou émis
doit être égale à une différence de niveau d’énergie de l’atome, donc à une transition énergétique
possible. Or, l’énergie de la lumière dépend de la longueur d’onde. Donc, la longueur d’onde des
photons susceptibles d’être absorbés ou émis doit être égale à des valeurs précises.
Absorption d’un photon
Emission spontanée d’un photon