TP TD Flambement :

TP TD Flambement :
Problème de stabilité
Objectif : Cette étude constitue un modèle simple du flambage des poutres
pour lequel on a réduit la déformation de la poutre a un « angle
concentré » au milieu de la poutre.
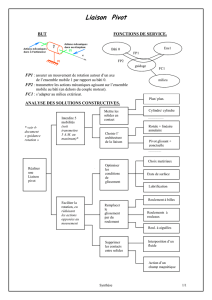
Soit un système de deux barres rigides identiques (OA et AB), de longueur ℓ.
L’angle  est orienté selon k et sépare l’axe horizontal de OA :  = (i, OA)
Le point O est fixe dans le repère Galiléen TO(i, j, k) et constitue une liaison pivot d’axe k
pour la barre OA. Le point B est astreint à glisser sur l’axe Ox entre 0 et 2ℓ, il constitue
également une liaison pivot. Le point A peut se déplacer sur le demi de cercle de rayon ℓ, de
centre O défini par x positif, il relie les deux barres par une liaison élastique de raideur  qui
crée un moment de torsion d’axe k lorsque  n’est pas nulle.
La force de pesanteur est négligée dans ce problème.
1) Rappelez brièvement les caractéristiques d’une liaison pivot et d’une liaison élastique,
puis exprimez le moment de torsion exercée en A pour   0.
On applique à présent une force horizontale en B :
i
FF
 )(
2) Avant d’appliquer en détail les lois physiques en jeu, décrivez les phénomènes
qu’intuitivement vous pensez observés suivant les valeurs de F (Répondre avant de
poursuivre !!)
3) Cinématique
a) Exprimez la vitesse de rotation de la barre OA et celle de AB dans TO.
b) Déterminez la vitesse des points O, A, B dans TO.
c) Exprimez la vitesse de rotation de AB par rapport à OA.
y
A
B
x
Ө
O
i
j
k
F

4) Exprimez les puissances des actions de liaisons :
a) Puissance des forces exercées sur la liaison pivot en O
b) Puissance des forces exercées sur la liaison élastique en A
c) Puissance des forces exercées sur la liaison pivot en B
d) Puissance totale
5) Exprimez l’énergie potentielle associée au système, ainsi que les expressions des
dérivés première et seconde par rapport à 
6) Déterminez graphiquement les conditions d’équilibre : Commentez les trois cas
possibles
7) Etudiez la stabilité des différents cas envisagés et réalisez le diagramme de bifurcation
correspondant à cette étude
Rappel sur la théorie des bifurcations : à partir d’un seuil, une nouvelle solution d’équilibre
apparaît et il y a échange de stabilité : la première solution d’équilibre qui était stable devient
instable et c’est la deuxième solution qui devient stable