fichier élève

Seconde – Physique partie A- Chap2- document élève
sesames 1/5 v9 - octobre 2007
Chapitre 2 : Outils de description de l'univers et du
système solaire
Activité 1 Répartition des planètes dans le système solaire
Lire le texte donné en annexe présentant sommairement le système solaire.
Le tableau qui suit peut être exploité durant tout le chapitre. Vous aurez à compléter la colonne vide au
cours de l’activité.
Astre
Diamètre
(en km)
Distance au soleil
(en millions de
km)
Distance au
soleil
(en km)
Période de
révolution
(en jours)
Étoile
Soleil
1 400 000
Planètes
telluriques
1. Mercure
4 800
58
88
2. Venus
12 200
110
225
3. Terre
12 750
150
365
4. Mars
6 700
230
687
Planètes
géantes
5. Jupiter
143 000
780
4333
6. Saturne
122 000
1 400
10760
7. Uranus
52 000
2 900
30600
8. Neptune
48 000
4 500
60190
1. Écrire avec tous les zéros nécessaires la valeur de la distance entre le Soleil et la Terre en
kilomètres.
2. Quel est l'inconvénient "pratique" d'une telle écriture ?
3. Proposer une "technique" pour écrire avec des chiffres cette même distance en kilomètres, sans
écrire trop de zéros.
4. Avec cette "technique" écrire de deux façons différentes la distance entre le Soleil et Neptune en
kilomètres.
Notation scientifique.
De façon plus générale, on peut écrire n'importe quel nombre selon un "format" qu'on appelle "notation
scientifique" : En notation scientifique, tout nombre est écrit
comme le produit d’un nombre compris entre 1 et 10 et d’une puissance de 10 :
a 10 n où 1  a < 10 et n un entier positif ou négatif.
Exemple : la valeur de la distance Soleil-Terre s’écrit 1,50.108 km.
5. Compléter la colonne vierge du tableau à l'aide de la notation scientifique.
-----------------------------------------
Activité 2 Un outil pratique pour . . . . . . . . . . . . . : l'ordre de grandeur
A- Questions préliminaires
1. Selon vous, quel est l’ordre de grandeur de la taille des objets suivants (cocher une case par objet)
fourmi :  un km  une dizaine de m  un m  un cm  un mm
pouce :  un km  une dizaine de m  un m  un cm  un mm
immeuble de 10 étages  un km  une dizaine de m  un m  un cm  un mm
2. A partir de ces exemples, indiquer selon vous à quoi peut servir l'ordre de grandeur.
3. Compléter le titre de l'activité.
-----------------------------------------

Seconde – Physique partie A- Chap2- document élève
sesames 2/5 v9 - octobre 2007
B- A quoi sert la notion d'ordre de grandeur en science ?
L'ordre de grandeur est un outil scientifique dont on peut avoir besoin :
1- Lorsqu'on veut faire des comparaisons rapides et approximatives de deux nombres qui sont très différents (on
dit qu'ils ne sont pas du même ordre) ;
2- Lorsqu'on veut situer différents nombres sur une très grande "échelle", généralement pour les comparer entre
eux.
C- Détermination d'un ordre de grandeur
On dispose d'une définition mathématique qui permet de déterminer l'ordre de grandeur d'un nombre.
L'ordre de grandeur d'un nombre a 10 n est une puissance de 10 proche de ce nombre. On
l'obtient en appliquant le critère suivant :
Si a < 5 alors l'ordre de grandeur du nombre est 10n : l'ordre de grandeur de 3,2.102 est 102.
Si a> 5 alors l'ordre de grandeur est 10n+1 : l'ordre de grandeur de 7,3.102 est 103.
Si a=5, on peut convenir que l'ordre de grandeur est 10n+1.
Ce critère est une convention et peut être modifié. On pourrait choisir une autre convention qui permettrait aussi de
comparer approximativement différents nombres entre eux. Par exemple, avec une autre convention, on pourrait dire que
l’ordre de grandeur du nombre a x 10n est 10n quel que soit a.
En physique, on utilise cette définition en l'adaptant à l'ordre de grandeur d'une valeur :
L'ordre de grandeur d'une valeur (= nombre + unité) est l'ordre de grandeur du nombre + l'unité.
D- Entraînement au passage d'une valeur à son ordre de grandeur
Donner les ordres de grandeurs des valeurs suivantes :
Valeur
Notation
scientifique
Ordre de
grandeur
Notation
scientifique
Ordre de
grandeur
1
Vitesse de la lumière
299 792 458 m/s
m/s
m/s
2
Distance Paris Nice par autoroute
930 km = 930.103 m
km
km
m
m
3
Masse de la tour Eiffel
7300 tonnes environ, soit 7300.103 kg
t
t
kg
kg
4
Hauteur de la tour Eiffel
312 m
m
m
5
Diamètre du soleil
1,4 millions de km = 1,4 .109 m
km
km
m
m
6
Durée d'une année en seconde
31 558 milliers de secondes
7
Rayon de l'atome d'hydrogène (le plus petit des atomes)
53 pm = 53.10–12 m
pm
pm
m
m
8
Diamètre de notre galaxie
9,5.1017 km = 9,5.1020 m
km
km
m
m
9
La masse d'eau de pluie tombant chaque année en France
330.109 t = 330.1012 kg
t
t
kg
kg
10
La distance Terre-Soleil
150.106 km = 150.109 m
km
km
m
m
11
Hauteur d’un arbre
15m
m
m
12
Volume d'eau nécessaire pour fabriquer une tonne de
papier : Environ 300 000 L
L
L
13
Taille moyenne d’un humain adulte
1m70
m
m
14
Masse de CO2 produite par une petite auto en 10000 km.
1380 kg
kg
kg
15
Longueur de la bactérie colibacille
2,5 µm = 2,5.10–6 m
µm
µm
m
m
16
Masse d'ordures ménagères par habitant en France
Environ 400 kg
kg
kg
17
Rayon du proton
1,2.10–15 m
m
m
18
Epaisseur d’un cheveu
80 µm = 80.10–6 m
µm
µm
m
m

Seconde – Physique partie A- Chap2- document élève
sesames 3/5 v9 - octobre 2007
E- Utilisation de la notion d'ordre de grandeur
1ère fonction : comparer rapidement
1. Calculer le rapport entre l'ordre de grandeur du diamètre de notre galaxie et l'ordre de grandeur
du diamètre du soleil.
2. Compléter la phrase suivante en français : notre galaxie est approximativement ………………
fois plus grande que le soleil.
2e fonction : situer différentes valeur sur une "échelle" d'ordre de grandeur.
3. Parmi les exemples proposés dans le tableau précédent, placer ci-dessous les valeurs de
distances en fonction de leur ordre de grandeur (comme sur l'exemple).
femtomètre
picomètre
nanomètre
micromètre
millimètre
mètre
kilomètre
mégamètre
gigamètre
téramètre
petamètre
examètre
zettam
ètre
fm
pm
nm
m
mm
m
km
Mm
Gm
Tm
Pm
Em
Zm
10-15
10-14
10-13
10-12
10-11
10-10
10-9
10-8
10-7
10-6
10-5
10-4
10-3
10-2
10-1
1
10
102
103
104
105
106
107
108
109
1010
1011
1012
1013
1014
1015
1016
1017
1018
1019
1020
1021
-----------------------------------------
Activité 3 Réalisation d'une maquette du système solaire dans le couloir
du lycée
On souhaite réaliser une maquette du système solaire dans le couloir du lycée.
Chaque binôme travaille sur deux planètes données : il doit déterminer les positions des planètes et leurs tailles
dans la maquette.
Pour l'échelle, on choisit d'utiliser la totalité du couloir pour y placer au moins Jupiter. On décide alors que la
distance Jupiter-Soleil vaudra . . . . . . . . . . . . . pour la maquette.
1. En déduire l'échelle et l'indiquer à la façon des géographes : 1:…………
2. A cette échelle, quel doit être le diamètre d'un objet représentant le soleil dans la maquette ? Quel objet
pourrait approximativement convenir ? On placera un tel objet à l'une des extrémités du couloir.
3. Calculer le diamètre de "vos planètes" et leurs distances au soleil dans la maquette.
4. Pour chacune de vos planètes, représenter la planète sur une feuille blanche (si ce n'est pas trop petit) et
indiquer dans le coin en haut à gauche :
 le diamètre réel et le diamètre à l'échelle (ou diamètre réduit) ;
 la distance réelle au soleil et la distance à l'échelle (distance réduite).
On pourra aussi choisir, parmi tous les objets sphériques disponibles, celui qui convient le mieux pour
représenter la planète et l'accrocher à un fil "invisible".
Placement des planètes : vous disposez soit du plan de l'étage du lycée (avec une échelle précisée) soit de
décamètres.
5. Si vous pouvez placer "vos planètes" dans le lycée, faites-le le plus précisément possible.
Sinon, indiquer approximativement, à l'aide de plans ou de cartes, où vous devriez les placer.
Questions d'exploitation
6. a) A quelle distance de l'objet représentant le soleil devrait-on placer à cette échelle l'étoile la
plus proche du soleil (Proxima du Centaure), située à 4,07.1013 km ?
b) Justifier à l'aide de la maquette, et éventuellement à l'aide d'un dictionnaire, l'affirmation
suivante : "le système solaire a une structure lacunaire".
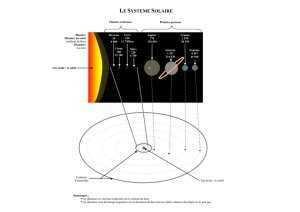
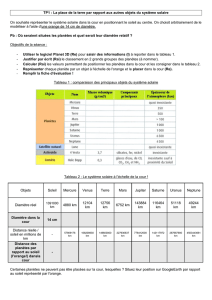
7. a) Le schéma du système solaire représenté dans le document annexe vous semble-t-il "à
l'échelle", c’est-à-dire respectant une même échelle pour toutes les orbites tracées ? Même
question pour le photo-montage à la fin du document annexe, au sujet des distances entre le
soleil et les planètes.
b) Sur le photo-montage, l’échelle a-t-elle été respectée pour les tailles des planètes ?

Seconde – Physique partie A- Chap2- document élève
sesames 4/5 v9 - octobre 2007
Activité 4 Vitesse de la lumière dans l'univers et application à la
désignation des distances
La vitesse de la lumière dans le vide vaut 3,00.108 m/s (ou noté aussi m.s-1), soit environ trois cent mille
kilomètres par seconde.
C’est une vitesse limite : il n’existe pas de vitesse supérieure.
Remarque : la vitesse de la lumière dans l’air est quasiment la même que dans le vide.
1. Le son se propage dans l'air à la vitesse de 340 m/s c'est-à-dire beaucoup plus lentement que la
lumière. Pour mieux percevoir l'écart entre la vitesse de propagation de la lumière et celle du
son, on raisonne sur l'analogie suivante :
 Le TGV, qui va à 300 km/h, soit 83,3 m/s, correspond à la lumière.
 On cherche un objet en mouvement pour correspondre au son.
Lumière
 TGV
Son
 ???
a. Selon vous (sans calcul et intuitivement), quel est l'objet qui convient le mieux :
 Un avion de chasse dans le ciel
 Une voiture sur autoroute
 Un cheval au galop
 Un marcheur (marche normale)
 Une limace
b. Pour que l'analogie soit convenable, quelle doit être la valeur de la vitesse de cet objet
qui correspond au son (en m/s).
c. Donner le résultat en cm/h.
d. Modifier éventuellement (en marquant la différence éventuelle avec une autre couleur)
votre prévision initiale.
2. Donner un exemple courant qui illustre la différence entre la vitesse du son et celle de la lumière
dans l’air.
-----------------------------------------
Activité 5 L'année de lumière : une unité de distance
Une année de lumière est la distance parcourue par la lumière dans le vide pendant une année.
Le symbole de cette unité de distance est a.l..
ATTENTION, l’année de lumière est bien une unité de distance et non de temps…
1. La lumière émise par Proxima du Centaure (étoile la plus proche de notre système solaire) met
4,3 années pour atteindre la Terre.
Quelle est la distance, en années de lumière, entre cette étoile et la Terre ?
2. Antarès est une étoile située à 170 années de lumière de la Terre.
a. Combien de temps la lumière émise par Antarès met-elle pour nous parvenir ?
b. Comment est-il possible que certains scientifiques pensent que cette étoile s'est déjà
éteinte alors qu'elle est encore visible dans le ciel ?
3. Calculer la distance en mètre parcoure par la lumière en une année.
4. En déduire la valeur d'une année de lumière en mètre. 1 a.l. = . . . . . . . . .m.
5. Quel est, en mètre, l'ordre de grandeur de l'année de lumière.
6. a. Calculer la distance, en kilomètre, entre Proxima du Centaure et la Terre.
b. A partir de cet exemple indiquer l’intérêt qu’il y a à exprimer les distances des astres en
année de lumière.
7. Combien de temps (en minutes) la lumière met-elle pour nous parvenir du Soleil ? Est-ce que
l'année de lumière est une unité adaptée pour la distance Soleil-Terre ? Proposer une autre unité
plus adaptée (ni l'année de lumière, ni le mètre).

Seconde – Physique partie A- Chap2- document élève
sesames 5/5 v9 - octobre 2007
Document annexe LES COMPAGNONS DU SOLEIL
La nuit, des milliers d’étoiles
scintillent dans le ciel. Toutes ces
étoiles font partie de notre galaxie, la
voie lactée. Le soleil, vieux de 5
milliards d'années environ, est une
étoile parmi elles. C’est l'étoile la
plus proche de la Terre. Autour de lui
gravitent huit planètes dont la Terre.
Comme la Terre, toutes les planètes
tournent sur elles-mêmes. Eclairées
par le soleil, elles nous renvoient une
partie de la lumière quelles reçoivent
et brillent dans le ciel. La plus connue
est Vénus, appelée improprement
" étoile du berger ". Contrairement
aux étoiles qui, chaque soir, se
retrouvent à la même place dans le
ciel, la position des planètes change,
d’où leur nom : planète signifie
« astre errant » en grec.
Les huit planètes du système solaire
sont, de la plus proche à la plus
éloignée : Mercure, Vénus, Terre,
Mars, Jupiter, Saturne, Uranus,
Neptune. Toutes ces planètes se
déplacent sur des orbites pratiquement
circulaires. Seule la Terre fait un tour
complet du soleil en 365 jours. Les
planètes du système solaire sont divisées
en deux grandes catégories.
On appelle planètes telluriques les
planètes qui ressemblent à la Terre
comme l'appellation le suggère (tellus =
terre, en latin). Mercure, Vénus, la Terre
et Mars sont ainsi toutes constituées d’une
matière rocheuse et leur surface est solide.
Leur taille n’est pas très importante et
elles ne possèdent pas beaucoup de
satellites (Mars en a deux, la Terre, un
seul). Elles circulent sur des orbites
relativement proches du soleil.
On appelle planètes géantes gazeuses les
quatre planètes largement plus grande et
plus lourde que la Terre : Jupiter, Saturne,
Uranus et Neptune. Jupiter, par
exemple, est onze fois plus grande que
la Terre et mille fois plus lourde. Ces
planètes sont essentiellement constituées
de gaz, et leur surface n’est pas dure.
Entourées d’anneaux et possédant de
nombreux satellites, elles circulent à des
distances du soleil plus importantes que
les planètes telluriques.
ou sur fond blanc :
Soleil
Soleil