Document

P a g e | 1
La pile et le condensateur Document : M.Moppert - CPF - Beyrouth
TS
Physique
Oscillations électriques
Exercice
résolu
Enoncé
L’exercice est composé de 8 questions contenant chacune 4 propositions. Pour chaque
proposition, écrivez VRAI ou FAUX dans le tableau en annexe. Aucune justification n’est
demandée. ATTENTION : chaque proposition est notée sur 0,25 pt (0 pt en cas de non réponse)
mais, au-delà d’une erreur dans une même question, chaque nouvelle erreur fera l’objet d’une
pénalité de – 0,25 pt dans cette question.
1. Circuit RL (1/2)
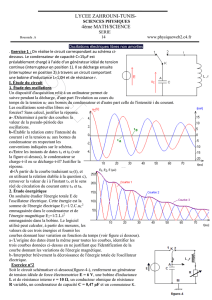
On réalise le circuit schématisé ci-
contre, dans lequel un générateur idéal
de tension de f.e.m E = 6,0 V est monté
en série avec une bobine d’inductance L
et de résistance r, et un conducteur
ohmique de résistance R = 50 .
Les deux voies d’un oscilloscope à
mémoire permettent d’enregistrer les
variations des tensions. On ferme
l’interrupteur K à la date t = 0 ms.
a) La bobine s’oppose aux variations de la tension dans le circuit.
b) En régime permanent, l’intensité du courant dans le circuit vaut environ 100 mA.
c) La résistance r de la bobine vaut environ 15 
d) L’inductance de la bobine vaut environ 60 mH.
2. Circuit RL (2/2)
On réalise le circuit ci-après (figure 1)
comprenant : un GBF (isolé de la terre),
un conducteur ohmique de résistance
R = 100  et une bobine d’inductance L et
de résistance négligeable par rapport à la
résistance R. A l’aide d’une interface et
d’un ordinateur, on visualise les variations
de la tension uBM en fonction du temps
(figure 2). La tension uAM a pour
valeur – 0,10 V pour t compris
entre 0 et 10 ms.
a) La tension aux bornes du conducteur ohmique a pour expression : uBM = R.i
b) La tension aux bornes de la bobine a pour expression uAM = L.i
c) L’inductance de la bobine a pour valeur L = 1,0 H.
d) La fréquence de la tension délivrée par le générateur vaut 50 Hz.

P a g e | 2
La pile et le condensateur Document : M.Moppert - CPF - Beyrouth
3. Circuit LC
On réalise le circuit ci-contre comprenant : une bobine d’inductance L et un
condensateur de capacité C. L’interrupteur K étant ouvert, la tension aux
bornes du condensateur est UAB = 10 V. On considère que la résistance de la
bobine et des fils de connexion est nulle.
A l’instant t = 0, on ferme l’interrupteur K. A l’aide d’un système informatique,
des enregistrements ont été effectués et ont donné les expressions
suivantes :
 uAB (t) = 10 cos (1,0 x 103 t) avec uAB (t) en V et t en s
 i(t) = 1,0 x 10-2 sin (1,0 x 103 t) avec i(t) en A et t en s
a) Les variations de uAB et de i au cours du temps correspondent à un régime pseudopériodique.
b) Avec les conventions du schéma, on peut écrire : i = C.
AB
du
dt
.
c) Le condensateur a une capacité C = 1,0 µF.
d) L’énergie totale emmagasinée dans le circuit a pour valeur E = 50 µJ.
4. Circuit RLC (1/2)
Le circuit ci-contre comporte un générateur idéal de tension de f.e.m
E, une bobine d’inductance L (de résistance négligeable), un
conducteur ohmique de résistance R ajustable de 0 à 10 k, un
condensateur de capacité C et un commutateur K.
 On place le commutateur en position 1 :
a) L’équation liant la tension uAM, sa dérivée par rapport au temps et
les caractéristiques du circuit s’écrit :
AM AM
du u E0
dt RC RC
.
 On bascule le commutateur en position 2 :
b) Quand le commutateur est dans cette position, le courant circule initialement dans le sens
indiqué sur le schéma.
c) On observe des oscillations forcées sur la voie 1 de l’oscilloscope.
d) Dans le cas ou R = 0, l’équation liant la tension uAM, sa dérivée par rapport au temps et les
caractéristiques du circuit s’écrit :
2AM AM
2
d u u 0
LC
dt 
.
5. Circuit RLC (2/2)
On considère le circuit ci-dessous. Le condensateur est initialement chargé et son armature A
porte une charge q0 = + 30 C. A l’instant t = 0, on ferme l’interrupteur K. On visualise alors les
tensions aux bornes du conducteur ohmique et du condensateur.

P a g e | 3
La pile et le condensateur Document : M.Moppert - CPF - Beyrouth
Données : C = 10 F et 2 = 10
a) A t = 0, la tension aux bornes du condensateur est d’environ 3,0 V.
b) A t = 2,0 ms, l’armature A porte la charge q = 10 C.
c) La tension de la courbe b est proportionnelle à l’énergie totale stockée dans le circuit.
d) La valeur de l’inductance est proche de 2,5 mH.
ATTENTION - Les trois questions suivantes concernent le montage ci-dessous :
6. On ferme l’interrupteur K1 pour charger le condensateur, le commutateur K2 étant en position
0 :
a) Il faut au moins 4,5 x 10-1 ms pour que le condensateur soit complètement chargé.
b) A la fin de la charge du condensateur, la tension uR est nulle.
c) A cause de la résistance R, les oscillations dans le circuit sont amorties.
d) Pour visualiser la tension uC sur un oscilloscope, il faut relier A à l’entrée de l’oscilloscope et B
à sa masse.
7. On ouvre ensuite l’interrupteur K1 et on place le commutateur K2 en position 1 à un instant
choisi comme origine des dates. Le graphique ci-dessous représente l’évolution de la tension
uC aux bornes du condensateur :
a) R.i +
q
C
= - L.
di
dt
b) La valeur de l’inductance de la bobine est L = 7,0 x 10-2 H.
c) Si on augmente la résistance R du conducteur ohmique, la pseudo-période T des oscillations va
diminuer.
d) A la date t = 10 ms, l’intensité i du courant dans le circuit est nulle.
0
1
2
K1
K2
C
R
E
uR
uL
uC
u
L
Module
électronique
A
B
C
E = 5,0 V
R = 100 
C = 9,0 x 10-1 F
Le condensateur est initialement déchargé et
la résistance de la bobine est négligeable.
i

P a g e | 4
La pile et le condensateur Document : M.Moppert - CPF - Beyrouth
8. On replace ensuite le commutateur K2 en position 0 et on ferme l’interrupteur K1 pour
recharger le condensateur. Le condensateur chargé, on ouvre l’interrupteur K1 et on place le
commutateur K2 en position 2 à un instant choisi comme nouvelle origine des dates. Le
graphique ci-dessous représente l’évolution de la tension uC aux bornes du condensateur :
a) u = uR + uC + uL
b) u = - R.i
c) L’énergie électrique emmagasinée par le condensateur est une fonction sinusoïdale du temps de
période 2,5 ms.
d) Le module électronique est un générateur idéal de tension.
Annexe
1
a
b
c
d
2
a
b
c
d
3
a
b
c
d
4
a
b
c
d
5
a
b
c
d
6
a
b
c
d
7
a
b
c
d
8
a
b
c
d

P a g e | 5
La pile et le condensateur Document : M.Moppert - CPF - Beyrouth
Corrigé
1. a) FAUX : la bobine s’oppose aux variations de l’intensité du courant dans le circuit.
b) VRAI : en régime permanent, la tension aux bornes du conducteur ohmique s’exprime par : U =
R.I
=> I =
U
R
soit I =
5, 0
50
= 1,0 x 10-1 A ou 1,0 x 102 mA
c) FAUX : loi d’additivité des tensions en régime permanent : E = r.I + R.I => r =
E R.I
I
Soit r =
1
6,0 50
1,0 10
= 10 
d) FAUX : à t = 0, E = uL + uR = uL = L.
0
di
dt
. Or : uR = R.i => i =
R
u
R
et
di
dt
=
R
du
1.
R dt
Donc, à t = 0 : E =
R
0
du
L.
R dt
=> L =
R
0
E.R
du
dt
R
0
du
dt
est le coefficient directeur de la tangente à l’origine de la courbe visualisée sur la voie 1.
Donc : L =
3
6,0x50
6,0 10
= 50 x 10-3 H ou 50 mH
1
A
FAUX
b
VRAI
c
FAUX
d
FAUX
2
A
FAUX
b
FAUX
c
FAUX
d
FAUX
3
A
FAUX
b
FAUX
c
VRAI
d
VRAI
4
A
FAUX
b
FAUX
c
FAUX
d
VRAI
5
A
VRAI
b
VRAI
c
FAUX
d
VRAI
6
A
VRAI
b
VRAI
c
FAUX
d
FAUX
7
A
VRAI
b
FAUX
c
FAUX
d
VRAI
8
A
FAUX
b
VRAI
c
VRAI
d
FAUX