exploration du système solaire - La Cosmologie précise, par

1
EXPLORATION DU SYSTÈME SOLAIRE
L’ ASSISTANCE GRAVITATIONNELLE
Philippe Magne
03 / 2001

2
EXPLORATION DU SYSTÈME SOLAIRE
L’ ASSISTANCE GRAVITATIONNELLE
L’exploration du système solaire implique la réussite d’une succession de rendez-
vous spatio-temporels avec les planètes en orbite : ce sont des cibles mouvantes,
tout bouge dans le système solaire, y compris le Soleil, car le centre de gravité du
système n’est pas confondu avec le sien, surtout à cause des planètes géantes.
On se propose, dans cet exposé, en simplifiant beaucoup, de donner un aperçu de
ce qu’est l’assistance gravitationnelle palliant les insuffisances de la propulsion
chimique.
A ce propos on comprendra toute l’importance de l’informatique pour résoudre un
aussi vaste problème.
Les possesseurs d’un ordinateur familial pourront reproduire, s’ils le désirent, la
simulation d’une assistance gravitationnelle obtenue au voisinage de Jupiter au
cours d’une mission devant atteindre Saturne.
Le logiciel à utiliser est QBASIC ou QB45.
INTRODUCTION
Le système solaire s’étend sur une quarantaine d’ UA, la distance Terre Soleil est
d’une UA ( Unité Astronomique )
L’unité UA vaut
11
1.4959787 10
mètres, en gros
150
millions de Km, 40 UA
correspondent à 6 milliards de kilomètres.
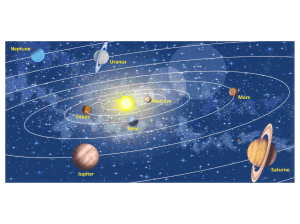
On se limitera aux planètes extérieures : Mars, Jupiter, Saturne, Uranus, Neptune,
Pluton ( Figure 1 ).
Les missions concernent à la fois ces planètes et leur cortège de satellites.
On montrera que, bien que la propulsion chimique ne permette pas de les atteindre,
l’assistance gravitationnelle y pourvoit.
Avant d’entrer dans le vif du sujet, rendons hommage aux astronomes dont la
patience et le travail extrêmement précis a permis l’établissement d’éphémérides
sans lesquels des objectifs aussi ambitieux ne pourraient être atteints.
QUELQUES ASPECTS DE L’ASTRONAUTIQUE
Le lancement d’une sonde d’exploration s’effectue en trois étapes que nous allons
décrire.
La première étape consiste, à proprement parler, à décoller de la Terre, ce qui
implique que la poussée du moteur fusée soit au moins supérieure au poids du
lanceur, lequel est fait de plusieurs étages.
Pour mieux comprendre cet aspect, montrons toute la différence qu’il y a entre le
poids et la masse, disons que le poids est une quantité relative à l’astre à partir
duquel s’effectue le lancement.
Poids = masse x accélération de la pesanteur à la surface de l’astre.

3
Figure 1

4
Rappelons que le champ de gravitation (synonyme d’accélération) à la surface de la
Terre est de l’ordre de 10 m / s² . Pour bien différencier le poids de la masse le
système international d’unités exprime la masse en kg et le poids (force) en
Newtons.
Prenons maintenant l’exemple de la navette américaine, sa masse au décollage est
de 2000 tonnes (
6
2 10 kg
), elle pèse 20 kilonewtons (
4
2 10 newtons
), à la surface
de Mars où le champ de gravitation n’est que de 3.82 m / s² elle ne pèserait que
7640 kilonewtons. Par contre, à la surface de la planète géante Jupiter où le champ
de gravitation est de 25.5 m / s² elle pèserait 51000 kilonewtons.
La première étape est donc bien de soulever le lanceur, ce qui implique une très
forte poussée qui s’avère de durée très courte devant la durée du voyage
interplanétaire.
La deuxième étape, se mouvoir dans l’espace interplanétaire, nécessite de libérer
la sonde de l’attraction terrestre en s’éloignant de la Terre, c’est à dire opposer à la
gravitation qui est une force morte une autre force qui est la force vive, autrement dit
opposer à l’énergie potentielle l’énergie cinétique, laquelle est proportionnelle au
carré de la vitesse ;
A ce propos, on se souviendra de l’existence des trois vitesses dites cosmiques :
 Pour une satellisation, environ 7900 m / s
 Pour une évasion définitive de la Terre 11200 m / s ( 1 )
 Pour une évasion définitive du Soleil 16600 m / s
Précisons que cette troisième vitesse cosmique a une valeur ambiguë si l’on ne
précise pas que son référentiel n’est pas le Soleil, mais la Terre, qui, elle même a
une vitesse orbitale d’environ 29786 km / s dans le référentiel du Soleil .
L’évasion solaire implique que l’on programme une trajectoire de façon que ces deux
vitesses aient la même direction et s’ajoutent .Il en résulte alors que la sonde se
trouve au périhélie d’une orbite parabolique dont le Soleil est au foyer.
Pour qu’il en soit ainsi, il faut que cette vitesse soit, dans le référentiel solaire,
2
fois la vitesse orbital de la Terre ( l’orbite de la Terre est quasi circulaire )
29786 2 42123
m / s ( 2 )
L’incrément de vitesse que doit procurer le moteur fusée après l’évasion terrestre est
de :
42123 – 29786 = 12337 m / s ( 3 )
La troisième vitesse cosmique par rapport à la Terre s’obtient par l’énergie cinétique
nécessaire qui est proportionnelle à :
11200² 12337² 16600
m / s ( 4 )

5
Compte tenu de la masse utile pour la mission, et donc finalement celle de toute la
sonde, il se peut que le savoir faire en impulsion spécifique soit insuffisant !
On peut estimer que l’état de l’art se situe un peu au dessous de 14550 m / s, valeur
révisable compte tenue des progrès de la technologie à venir.
Tous calculs faits on peut estimer réalisable une vitesse comprise entre 9000 et
9500 m / s, dans ce qui suit nous adoptons 9277 m / s ce qui donne dans le
référentiel solaire :
29786 + 9277 = 39063 m / s ( 5 )
Dans ces conditions la sonde se trouve au périhélie de son orbite solaire à une UA
du Soleil, elle poursuit sa route en chute libre soumise seulement au champ de
gravitation du Soleil.
Elle décrit une orbite elliptique dont l’excentricité « e » s’obtient par la formule
suivante :
(vitesse"périhélie")² (39064)²
e 1 1 0.72
(vitesse"circulaire")² (29786)²
( 6 )
La troisième étape dépend des choix suivants concernant la planète à atteindre :
 ou bien on freine le mouvement pour se poser sur cette planète
 ou bien on ajuste la vitesse de la sonde par rapport à la planète pour qu’elle
orbite autour de celle-ci
 ou on décide seulement de la frôler de façon particulière, pour que sa chute
vers cette planète lui procure un accroissement de vitesse par rapport au
Soleil et donc d’aller plus loin, c’est cela l’Assistance gravitationnelle
Pour optimiser cette étape, l’ordinateur est un outil indispensable, il permet d’ajuster
la distance minimum de passage auprès de la planète, ce paramètre est fondamental
pour atteindre une autre planète encore plus éloignée.
Seule l’informatique permet cette optimisation car il n’y a pas de solution analytique
que l’on puisse déduire de l’équation de Newton.
CALCUL DE LA TRAJECTOIRE PAR ORDINATEUR
On utilise, bien entendu, la loi de Newton qui stipule que le champ de gravitation est
proportionnel à la masse de la planète attractrice et inversement proportionnel au
carré de la distance par rapport à son centre de gravité.
D’emblée, faisons la remarque que la sonde exploratrice est si petite par rapport aux
planètes que sa masse n’intervient pas dans le calcul du champ de gravitation.