courants et tensions variables

582693614 Page 1 sur 6
Cours-TD n°2 IMRT2 2008-2009 REGIMES SINUSOIDAUX PERMANENTS
Ce cours-TD est le prolongement du TP « courants et tensions variables » fait en première année.
1. RAPPELS : COURANTS ET TENSIONS VARIABLES
Les tensions et intensités variables ont des valeurs non constantes au cours du temps .
1.1. Tensions variables particulières
1.1.a. Tension alternative
C’est une tension qui change de signe au cours du temps : elle est donc alternativement positive
puis négative.
 Une tension alternative peut également être symétrique quand elle varie de la même
manière ( ou symétriquement ) dans les valeurs positives et négatives.
1.1.b. Tension périodique
C’est une tension qui se reproduit identique à elle-même au cours du temps ; ceci se produit toutes
les périodes : on note la période T ; son unité est la seconde .
On définit également la fréquence f de la tension : c’est le nombre de périodes par seconde ; on
peut donc la calculer par la relation
1
fT
; l’unité de fréquence est le Hertz , de symbole Hz .
 Remarque : 1 Hz = 1 s-1
1.2. Grandeurs caractérisant les tensions variables
Préalable : les notations indiquées dans ce paragraphe sont impératives et doivent absolument
être apprises et respectées.
1.2.a. Valeur instantanée d’une tension variable
La valeur instantanée u est la valeur que prend la tension variable à un instant t donné : on la
note en minuscules : on la visualise en général à l’oscilloscope
1.2.b. Valeur efficace d’une tension variable
C’est la tension continue qui provoquerait la même dissipation d’énergie calorifique par effet
Joule que la tension variable pendant la même durée ; on la mesure avec un voltmètre en position
AC+DC ( alternative current + direct current )
 On la note U ou Ueff
1.2.c. Valeur moyenne d’une tension variable
C’est la tension continue qui provoquerait le même déplacement de charges que la tension
variable pendant la même durée ; on la mesure avec un voltmètre en position DC ( direct current )
 On la note <U> ou Umoy
1.3. Un cas particulier très important : les tensions sinusoïdales
Les tensions sinusoïdales sont symétriques et périodiques.
La valeur instantanée d’une tension sinusoïdale s’exprime ainsi :
max 2
.sin( . )u U t
T
 Umax est la valeur maximale de la tension ( ou amplitude )
 (
2.t
T
) est sa phase à l’instant t
 ( ) est sa phase à l’instant t=0 ( ou phase à l’origine )

582693614 Page 2 sur 6
Dans ce cas particulier de la tension sinusoïdale , il existe une relation simple entre U ( la valeur
efficace de la tension ) et Umax ( sa valeur maximale ) :
max
2
U
U
1.4. Les intensités variables
Tout ce qui a été dit dans les paragraphes précédents pour les tensions variables peut être
généralisé pour les intensités des courants variables ( non constants dans le temps ).
On pourra donc de la même manière définir pour un courant variable :
 Son intensité instantanée i
 Les valeurs efficace I et moyenne Imoy de cette intensité variable
De même les courants qui parcourent les circuits électriques alimentés par le secteur ont des
intensités sinusoïdales d’expression
max 2
.sin( . )i I t
T
et de valeur efficace
max
2
I
I
2. LES DIPOLES EN REGIME CONTINU
2.1. Rappels ( vus au TP n°2 de 1ère année )
La caractéristique d’un dipôle est la courbe reliant les variations de la tension UAB à ses bornes
en fonction de l’intensité du courant I qui le traverse ( il faut alors préciser les conventions
d’orientation de la tension et du courant ) .
Quelques propriétés particulières des dipôles :
 Caractéristique passant par l’origine ( UAB = 0 quand I =0 ) : dipôle passif
 Caractéristique ne passant pas par l’origine ( UAB 0 quand I =0 ) : dipôle actif
 Caractéristique symétrique par rapport à l’origine : dipôle symétrique ( son
comportement est identique quel que soit son sens de branchement )
2.2. Le conducteur ohmique
 La caractéristique d’un conducteur ohmique est une droite passant par l’origine ; on en
déduit la relation simple : UAB = R. I qui est la loi d’Ohm.
Conditions d’application de cette loi :
 Le courant rentre dans le dipôle par la borne A (c’est la
convention récepteur )
 R est la résistance du conducteur ohmique ( Unité de R :
Ohms ( ) si UAB est en Volts et I en A )
2.3. Le condensateur
Un condensateur est constitué de deux armatures métalliques très proches l’une de l’autre et
séparées par un isolant (papier paraffiné, air, électrolyte gélifié pour les condensateurs chimiques).
D’un point de vue électrique, c’est donc un circuit ouvert.
Charge du condensateur :
Quand on soumet un condensateur à une tension continue, ses armatures
accumulent simultanément des charges de signes contraires en quantités égales . Elles
se chargent progressivement jusqu’à une charge maximale
Le courant électrique circule donc pendant le temps de la charge. Il est
maximum au début de la charge puis diminue progressivement jusqu’à devenir
nul.
B
R
I
UAB
A
+
courant
électrons

582693614 Page 3 sur 6
Condensateur chargé :
Quand le condensateur est complètement chargé, le courant ne circule plus et il existe entre ses
armatures une tension U proportionnelle à la charge commune Q des
armatures (charge du condensateur) ( la tension atteinte en fin de charge
est égale à celle du générateur )
U et Q étant des grandeurs proportionnelles les rapports
Q
U
et
U
Q
sont ………….
On définit la capacité du condensateur C =
Q
U
Unités : C en farad (F) ; Q en coulomb (C); U en volt (V)
 Remarques : 1 F est une valeur très élevée de capacité ; les capacités sont exprimées le
plus souvent en F , nF et pF
 1 F(microfarad) = ….. F ; 1 nF(nanofarad) = ….. F ; 1pF (picofarad) = …..F
Calculer la charge finale d’un condensateur de capacité 100 F soumis à une tension de 5 V .
Calculer la charge finale d’un condensateur de capacité 500 F soumis à une tension de 5 V .
Calculer la charge finale d’un condensateur de capacité 100 F soumis à une tension de 10 V .
Décharge du condensateur :
Si on relie le condensateur chargé à un circuit fermé, les charges accumulées sur les armatures
s’écoulent progressivement dans le circuit jusqu’à devenir nulles : le
condensateur se décharge.
Le courant électrique circule donc pendant le temps de la décharge. Il est
maximum au début de décharge puis diminue progressivement jusqu’à devenir
nul.
En fin de décharge , la charge Q du condensateur est …….., la tension U
à ses bornes est …………….
Rapidité de charge ( ou de décharge ) :
La durée de la charge ( ou de la décharge ) d’un condensateur dépend de sa capacité C et de la
résistance R du circuit qui l’alimente : elle est sensiblement égale à 5.RC.
 Calculer ( en s puis en ms ) la durée de charge ( ou de décharge ) d’un condensateur de
capacité 20 nF à travers une résistance de 200 k ?
 Oscillogramme de charge (par une tension de 3 V) de décharge
3.
+Q
-Q
courant
R
+Q
-Q
U
+

582693614 Page 4 sur 6
3. LES DIPOLES EN REGIME SINUSOÏDAL PERMANENT
3.1. Comment caractériser le comportement d’un dipôle en
régime sinusoïdal ?
3.1.a. Régime sinusoïdal permanent
Quand un dipôle est soumis à une tension sinusoïdale de façon permanente, on dit qu’il est en
régime sinusoïdal permanent ( ou en régime sinusoïdal forcé ).
On observe alors que la tension u aux bornes d’un dipôle et l’intensité i du courant qui le
traverse sont également des grandeurs sinusoïdales de même fréquence f que la fréquence imposée par
le générateur sinusoïdal qui l’alimente.
Le comportement dipôle est forcément différent de celui qu’il peut avoir en régime continu,
puisque la tension qui l’alimente ne cesse de changer .
 Pour la tension du secteur ( U = 220 V efficaces ; f = 50 Hz ), combien de fois par seconde la
tension d’alimentation change-t-elle de sens ?
Entre quelles valeurs extrêmes évolue-t-elle ?
 Combien de fois par seconde une tension de fréquence 1 kHz change-t-elle de sens ?
Même question quand sa fréquence vaut 10 kHz puis 100 kHz .
On conçoit bien qu’un dipôle n’aura sans doute pas le même comportement quand sa fréquence
d’alimentation augmente. En effet, si on augmente la fréquence du générateur, cela impose au dipôle
d’évoluer de plus en plus vite et de changer de plus en plus vite d’état.
Dans le cas du régime sinusoïdal permanent , on étudiera comment varie le comportement du
dipôle quand on fait varier la fréquence qui l’alimente.
3.1.b. Impédance et déphasage
Pour comprendre le fonctionnement du dipôle, on va donc étudier :
 La tension à ses bornes :
max 22
.sin( . ) . 2.sin( . )u U t U t
TT
 L’intensité du courant qui le traverse :
max 22
.sin( . ') . 2.sin( . ')i I t I t
TT
 Pour faire cette étude, on utilise ( comme en continu ) la convention récepteur pour le
fléchage de u et de i.
 Compléter sur le schéma ci-contre le fléchage de i en respectant
la convention récepteur
Pour caractériser simplement u et i , on étudie deux grandeurs : le déphasage de la tension u par
rapport au courant i ( noté
/ui
) et l’impédance du dipôle ( notée Z ).
A. Impédance du dipôle
L’impédance Z d’un dipôle est défini par la relation
U
ZI
( U : valeur efficace de la tension u à ses bornes ; I : valeur efficace de l’intensité i qui le parcourt )
dipôle
i
u

582693614 Page 5 sur 6
 Remarque : on peut faire l’analogie entre la définition de la résistance en continu
U
RI
et de
l’impédance en sinusoïdal
U
ZI
 L’unité de l’impédance est par conséquent la même que celle de la résistance : ………….. de
symbole ………………. ( à condition que U soit exprimée en …….. et I en ……… )
 En continu , on avait également défini la conductance G par
1
GR
( unité
1
) ; en sinusoïdal,
on définit de même l’admittance A d’un dipôle par
1
AZ
( unité
1
) .
 Pour mesurer l’impédance d’un dipôle , comment doit-on procéder d’un point de vue
expérimental ?
B. Déphasage de u par rapport à i
Mathématiquement , on définit le déphasage
/ui
comme la différence entre la phase de
2
. 2.sin( . )u U t
T
et celle de
2
. 2.sin( . ')i I t
T
.
On a par conséquent
/.................. .................. .... .... ui
 Voici quelques cas particuliers de déphasage :
 u et i sont en phase
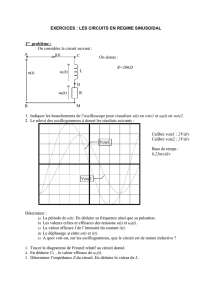
 Déterminer, la période, la fréquence et la valeur efficace
de u et de i
 On trouve ce cas pour des déphasages égaux à 0, mais
également 2 , 4 , 6 2 , -4 , -6 etc… car la période de
la fonction sinus est égale à 2 ( un déphasage de 2 ne
change donc rien )
Conclusion : un décalage ( en temps ) d’une période équivaut à un déphasage ( en phase ) de 2 radians.
 u et i sont en opposition de phase
 Déterminer, la période, la fréquence et la valeur efficace
de u et de i
 On trouve ce cas pour des déphasages égaux à , 3 , 5 ,
- , -3 , - 5 etc…