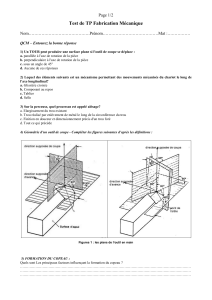
3.9 Mo - La Cosmologie précise, par Philippe Magne

1
TROUS NOIRS 2
Philippe Magne
( texte initial de 2000 )

2
Introduction
Trous noirs 1 montre que l’issue fatale des étoiles géantes est de devenir trous
noirs entourés d’un horizon qui se comporte comme une censure cosmique rendant
invisible une singularité ponctuelle de l’espace temps.
Dans le proche voisinage extérieur à cet horizon, le champ de gravitation est
énorme, l’espace temps est fortement courbé, la capture et l’orbite de particules
nécessitent un traitement relativiste.
Trous noirs 2 traite ce problème à l’aide du potentiel effectif qui sera d’abord décrit
dans la condition non relativiste en mécanique de Newton.
Ensuite cette notion sera développée dans la condition ultra relativiste à l’aide de la
métrique de Schwarzschild.
Einstein considérait que la métrique de Schwarzschild est une très bonne
approximation de la théorie géométrique de la gravitation.
_________________________________________________________
La table des matières se trouve à la fin du texte

3
1 Rappels de la notion de potentiel effectif en mécanique de Newton
Le potentiel effectif facilite considérablement l’analyse du mouvement d’une petite
masse d’épreuve ne participant pas au champ de gravitation, voire très peu quand la
masse centrale est prépondérante et génère une force centrale attractive.
Dans un espace vide où ne se produit aucun frottement, il n’existe que deux sortes
de trajectoires possibles :
Hyperboliques
Ouvertes
Paraboliques
Elliptiques
Fermées
Circulaires
En général la force centrale est dirigée vers une masse importante
M
placée à
l’origine du référentiel, qui attire une petite masse
0
m
, si petite qu’elle n’intervient
pas dans le champ de gravitation.
1.1 Position du problème
La vitesse
La vitesse
V
de
0
m
( figure 1 ), dans un système de coordonnées polaires
r,
a
deux composantes, de sorte que
222
r
V V V
Figure 1

4
Les forces
La force centrale d’attraction
a
F
est toujours dirigée suivant
r
, on la dit centrale
car
M
ne produit pas de couple .
Figure 2
Son module, vaut, d’après la gravitation Newtonienne :
0
a2
GMm
Fr
M
en kg
0
m
en kg
r
en mètres
G : constante universelle de la gravitation ( CUG ) =
11
6.67 10
La force d’inertie
I
F
centrifuge a un module qui vaut :
2
0
imV
Fr
avec
d
Vr
dt
Les lois de conservation
Les deux grandeurs qui se conservent pendant un mouvement sans frottement sont :
L’énergie totale, somme de l’énergie cinétique et de l’énergie potentielle.
Le moment cinétique dont le module est :
0
J m r V
1 .2 Potentiels dont dérivent
a
F
et
i
F
Potentiel
a
U
de
a
F
: c’est le travail qu’il faudrait fournir pour déplacer
0
m
depuis
un point situé à la distance
r
de O jusqu’à l’infini.

5
C’est une définition qui permet de se débarrasser de la constante d’intégration en
l’annulant.
a a 0 2
rr
dr
U F dr GMm r
0
aGMm
Ur
Potentiel
i
U
de
i
F
: la même définition conduit à un potentiel de signe négatif
puisque la force
i
F
tend à éloigner
0
m
de o.
ii
r
U Fdr
Plaçons nous dans la condition où le module du moment cinétique est constant et en
utilisant la formule écrite à la page précédente, on en déduit la vitesse
V
puis la
force
i
F
.
0
J
Vmr
222
00
i2 3 3
00
mV mJ J
Fr m r m r
D’où :
22
i32
00
r
J dr J
Um r 2m r
1. 3 Le Potentiel effectif
eff
U
est la somme de
a
U
et de
i
U
20
eff 2
0
GMm
J
U2m r r
Ce potentiel peut être positif ou négatif lorsque
r
varie de 0 à l’infini