Les médiatrices d`un triangle

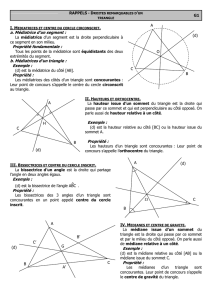
Les médiatrices d'un triangle
Définition : la médiatrice d'un segment est la droite perpendiculaire à ce
segment et passant par le milieu de ce segment.
Propriété : la médiatrice d'un segment [AB] est l'ensemble des points
situés à la même distance de A et de B (on dit équidistants de A et de B).
L'expression médiatrices d'un triangle désigne les médiatrices des côtés
du triangle. Un triangle a donc trois médiatrices.
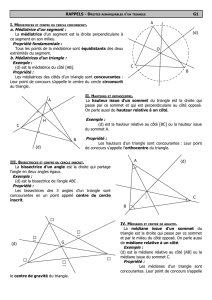
. Le cercle circonscrit à un triangle
Les trois médiatrices d'un triangle sont concourantes. Leur point de concours
est à la même distance des trois sommets du triangle et c'est le seul point ayant
cette propriété.
Il est donc le centre du cercle passant par les trois sommets du triangle.
Remarques :
— ce cercle est appelé cercle circonscrit au triangle. On dit quelquefois : le
triangle est inscrit dans le cercle ; le mot circonscrit vient du latin et signifie :
« écrit autour » (de même, inscrit signifie : « écrit dans ») ;
— en pratique, il suffit de construire deux médiatrices pour trouver le centre du
cercle circonscrit.
Les bissectrices d'un triangle
Définition : la bissectrice d'un angle est la droite qui partage cet angle en
deux angles de même ouverture.
Propriétés :
— la bissectrice de l'angle est l'axe de la symétrie qui échange les deux
demi-droites [Ox) et [Oy) ;
— les points de la bissectrice de l'angle sont équidistants des supports des
demi-droites [Ox) et [Oy).
La deuxième propriété permet de justifier la construction, à la règle et au
compas, de la bissectrice d'un angle b.
Propriété
Les trois bissectrices d'un triangle sont concourantes. Leur point de concours
est à la même distance des trois côtés du triangle ; il est donc le centre du
cercle tangent aux trois côtés du triangle.

Remarque : ce cercle est appelé cercle inscrit dans le triangle. Le mot inscrit
vient du latin et signifie « écrit dedans ».
Les hauteurs d'un triangle
Une hauteur d'un triangle est une droite qui passe par un sommet de ce
triangle et est perpendiculaire au support du côté opposé à ce sommet.
Ainsi construire la hauteur passant par A dans le triangle ABC revient à
construire la perpendiculaire à la droite (BC) passant par A.
Remarques :
— sur la figure 1, A' s'appelle le pied de la hauteur issue de A ;
— le mot hauteur désigne aussi le segment joignant un sommet et le pied de la
hauteur issue de ce sommet (le segment [AA'] sur la figure 1) ;
— le mot hauteur désigne encore la longueur du segment (la longueur AA' sur la
figure 1). C'est dans ce sens qu'il faut le prendre lorsqu'on dit : l'aire d'un
triangle est égale à la moitié du produit de la base par la hauteur ;
— dans un triangle, il y a trois hauteurs (autant que de sommets) ;
— la hauteur issue d'un sommet ne coupe pas toujours le côté opposé à ce
sommet.
L'orthocentre d'un triangle

Dans un triangle les trois hauteurs sont concourantes. Leur point de concours
est appelé l'orthocentre de ce triangle.
Remarques : en pratique, il suffit de tracer deux hauteurs pour trouver
l'orthocentre.
Les médianes d'un triangle
Une médiane d'un triangle est une droite qui passe par un sommet du triangle
et le milieu du côté opposé à ce sommet.
Remarques :
— le mot médiane désigne aussi le segment joignant un sommet et le milieu
du côté opposé à ce sommet (le segment [AA'] sur la figure 1) ;
— dans un triangle, il y a trois médianes (autant que de sommets) ;
— une médiane partage un triangle en deux triangles de même aire.
Le centre de gravité d'un triangle
Dans un triangle les trois médianes sont concourantes. Leur point de
concours est appelé centre de gravité du triangle.
Remarque : en pratique, il suffit de tracer deux médianes pour trouver le
centre de gravité.

RESUME
MEDIATRICE D’1
SEGMENT
HAUTEUR D’1
TRIANGLE
BISSECTRICE D’1
ANGLE
MEDIANE
D’1TRIANGLE
Droite à ce segment
,passant par le milieu du
segment
Droite passant par
le sommet,
Au côté opposé de
ce sommet
Droite qui partage
l’angle en 2 angles
égaux
Droite qui passe par
1sommet et le milieu
du côté opposé à ce
sommet
Les 3 médiatrices d’1
triangle sont
concourantes= leur point
de concours est le centre
du cercle circonscrit(écrit
autour)
Dans 1 triangle les
3 hauteurs sont
concourantes =
leur point de
concours est appelé
orthocentre
Les 3 bissectrices d’1
triangle sont
concourantes = leur
point de concours est le
centre cercle inscrit
dans le triangle (écrit
dedans)
Dans 1 triangle les 3
médianes sont
concourantes = leur
point de concours est
appelé centre de
gravité du triangle