tp 3 de physique : mouvement d`un solide, exploitation de videos

TP 3 DE PHYSIQUE : MOUVEMENT D’UN SOLIDE, EXPLOITATION DE VIDEOS
ETUDE D’UN MOUVEMENT DE ROTATION UNIFORME
1. Acquisition des points avec le logiciel Regavi.




Ouvrir le logiciel Regavi, choisir lecture d’un fichier AVI ou MPEG
Cliquer sur l’icône Ouvrir puis ouvrir le fichier Rot1 se trouvant dans le répertoire vidéos TP 2 sur le bureau.
Cliquer sur Origine pour choisir l’origine du repère : choisir l’axe de rotation du disque.
Régler l’échelle en cliquant sur l’icône Echelle. Cliquer successivement sur deux points séparés d’une distance
connue et renseigner la fenêtre de dialogue qui s’affiche. Ici, le diamètre du disque est de 0,60 m
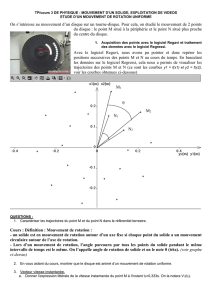
On va étudier le mouvement de deux points du disque : un point de la périphérie noté M (point noir sur le repère blanc) et
un point plus proche du centre, noté N. La durée entre 2 images est ici de τ = 66,7 ms.





Choisir zoom x2.
Choisir 2 points/image et cliquez sur l’icône Mesures.
Pointer successivement les positions des 2 points l’un après l’autre (le point M puis le point N).
Sans fermer la fenêtre de Regavi, ouvrir le logiciel Regressi.
Dans la fenêtre Regavi, cliquer sur l’icône Regressi.
2. Traitement avec le logiciel Regressi.


Cliquer sur l’icône
pour afficher la fenêtre des graphiques.
Visualiser les trajectoires des points M et N : ce sont les courbes y1 = f(x1) et y2 = f(x2). Pour choisir les
grandeurs en abscisse et en ordonnée, il faut cliquer sur l’icône
(désélectionner l’option abscisse unique).
QUESTIONS :
1. Caractériser les trajectoires du point M et du point N dans le référentiel terrestre.
2. Montrer que le disque est animé d’un mouvement de rotation uniforme.
3. Vecteur vitesse instantanée.
a. Donner l’expression littérale de la vitesse instantanée du point M à l’instant t 5=0,333s. On la notera V1(t5).
On remarque que pour calculer cette vitesse, il faut déterminer la distance M 4M6. Le logiciel Regressi comme tous les
tableurs permet de calculer automatiquement cette distance… et même toutes les distances Mi-1Mi+1. Il suffit de
remarquer qu’on peut calculer M4M6 à partir des coordonnées des points M4 (x1(t4) ; y1(t4)) et M6 (x1(t6) ; y1(t6)) déjà en
mémoire dans Regressi. Le logiciel donc permet aussi de calculer automatiquement la vitesse du point M à tout
instant.

Cliquer sur

Cliquer sur
pour programmer le calcul des vitesses V1(ti). Sélectionner grandeur calculée. Le symbole de la
grandeur est v1, elle est exprimée en m/s.
L’expression à entrer sans erreur est : v1=sqrt((x1[i-1]-x1[i+1])^2+(y1[i-1]-y1[i+1])^2)/ (t[i+1]-t[i-1])
Appuyer sur OK. La nouvelle colonne v1 est apparue dans l’onglet Variables. On peut lire la valeur de V1(t5) à la
ligne n°5.


pour accéder à la fenêtre des grandeurs.
b. Donner la valeur des vitesses V1(t2), V1(t5), V1(t8).
c.
On veut maintenant que le logiciel détermine la vitesse du point N à tout instant : elle sera notée V2(t). En
suivant la même procédure qu’au a), créer une grandeur calculée v2 exprimée en m/s et calculée à l’aide de
l’expression : v2=sqrt((x2[i-1]-x2[i+1])^2+(y2[i-1]-y2[i+1])^2)/ (t[i+1]-t[i-1])
d. Donner la valeur des vitesses V2(t2), V2(t5), V2(t8).
e. Sur l’enregistrement imprimé, tracer les vecteurs vitesse des points M et N aux instants t2 et t8.
4. Mesure de la vitesse angulaire  du point M.
a. Tracer les droites OM4 et OM6. Mesurer l'angle 5 (en radiants) entre ces deux droites.
Calculer la vitesse angulaire 5 du point M lorsqu’il occupe la position M5 :
b. En utilisant la même méthode, calculer la vitesse angulaire du point N lorsqu’il occupe la
position N5. Que remarquez-vous ?
c. Cette vitesse angulaire est-elle constante au cours du temps ? Justifier.
5
5
2
5. Etablir une relation entre v et .
Le rayon de la trajectoire du point M est R1 = OM = 0,26 m. Le rayon de la trajectoire du point N est R2 = ON = 0,15 m.
a. A l’aide de Regressi, créer deux grandeurs permettant de calculer les grandeurs w1 = v1 / R1 et w2 = v2 / R2.
b. Comparer les valeurs obtenues à celles de la vitesse angulaire mesurée au 4).
c. Peut-on en déduire une relation entre la vitesse linéaire V(t) d’un point, la vitesse angulaire  et le rayon R de la
trajectoire de ce point ?
v1=sqrt((x1[i-1]-x1[i+1])^2+(y1[i-1]-y1[i+1])^2)/ (t[i+1]-t[i-1])
v2=sqrt((x2[i-1]-x2[i+1])^2+(y2[i-1]-y2[i+1])^2)/ (t[i+1]-t[i-1])
w1=v1/0.26
w2=v2/0.15