BTS IRIS Commentaires - site académique de Sciences Physiques

S.T.S Informatique et Réseaux pour l’Industrie et les Services techniques
Physique appliquée : Réflexions pédagogiques. Thème II version du 27/02/03
Document issu d’un travail collectif dirigé par Joëlle JACQ IA-IPR Académie d’Aix-Marseille Page 1 sur 8
II.1. Propriétés temporelles du signal.
Eléments d’analyse du programme :
On s’intéresse à la réponse s(t) d’un
système linéaire analogique à une
entrée e(t).
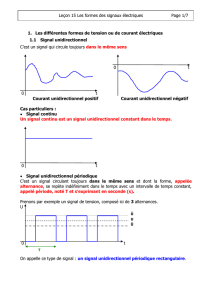
1er Cas : signaux sinusoïdaux.
La grandeur d’entrée e(t) variant de façon sinusoïdale en fonction du temps peut s’écrire, par exemple, sous la forme :
e(t) =
tE sin2
Par définition,
- la phase de cette grandeur est l'argument de la fonction sinusoïdale utilisée : ici c’est
)( t
- la phase à l’origine est la valeur de la phase lorsque la variable t est nulle : ici c'est
)(
La notion de différence de phase intervient lorsque plusieurs grandeurs sinusoïdales synchrones sont étudiées :
e(t) =
tE sin2
s(t) =
tS sin2
On définit alors la différence de phase entre les signaux s(t) et e(t) par la différence = (β – α). En général, la phase
origine de l'une des grandeurs, prise pour référence, est choisie nulle.
Comme il arrive que souvent, par abus de langage, on en vienne à confondre les notions de « déphasage » et de
« différence de phase », nous proposons de bien faire une distinction entre les cas suivants :
 le cas général où l’entrée e(t) et la sortie s(t) sont de natures quelconques (cas de l’étude d’un
système analogique linéaire en régime sinusoïdal) : on utilisera alors exclusivement l’expression
« différence de phase »
 le cas particulier où l’entrée e(t) = u(t) est la tension bornes d’un dipôle linéaire et s(t) = i(t) est
l’intensité du courant qui le traverse : on utilisera alors le mot « déphasage » et la définition correspondante.
On relira avec profit les commentaires des programmes des classes de première STI Génie électronique et Génie
électrotechnique dont la version rénovée en 2002 est téléchargeable à l’adresse : www.eduscol.education.fr/prog/
entrée
e(t)
sortie
s(t)
système
linéaire
Thème II. ANALYSE DU SIGNAL.
II.1. Propriétés temporelles du signal.
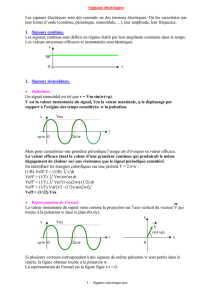
Représentations temporelle et complexe d’un signal sinusoïdal.
Valeur moyenne d'un signal périodique.
II.2. Propriétés fréquentielles du signal.
Représentation fréquentielle d’un signal périodique.
II.3. Propriétés énergétiques du signal.
Puissance instantanée. Puissance moyenne transportée par un signal périodique.
Valeur efficace d’un signal périodique.

S.T.S Informatique et Réseaux pour l’Industrie et les Services techniques
Physique appliquée : Réflexions pédagogiques. Thème II version du 27/02/03
Document issu d’un travail collectif dirigé par Joëlle JACQ IA-IPR Académie d’Aix-Marseille Page 2 sur 8
 est la différence de phase entre s(t) et e(t)
La différence de phase  représente l’argument de la transmittance complexe T définie par
E
S
T
, relation dans laquelle E et
S sont respectivement les grandeurs complexes associées aux grandeurs sinusoïdales e(t) et s(t).
La différence de phase  présente donc un caractère algébrique :  = Arg( T ) = Arg( S ) – Arg( E )
< 0, car sin( t + ) s’annule pour t1 > 0. Or = - t1 donc < 0
> 0, car sin( t + ) s’annule pour t0 < 0. Or = - t0 donc > 0
e( )
s( ) en
retard
s( ) en
avance
= t
t0
t1
s( )
e( ) en
avance
e( ) en
retard
= t
> 0, car sin( t - ) s’annule pour t1 > 0. Or = t1 donc > 0
< 0, car sin( t - ) s’annule pour t0 < 0. Or = t0 donc < 0
t0
t1
Référence sur l’entrée e(t) : e(t) =
tE sin2
s(t) =
tS sin2
Référence sur la sortie s(t) : e(t) =
tE sin2
s(t) =
tS sin2

S.T.S Informatique et Réseaux pour l’Industrie et les Services techniques
Physique appliquée : Réflexions pédagogiques. Thème II version du 27/02/03
Document issu d’un travail collectif dirigé par Joëlle JACQ IA-IPR Académie d’Aix-Marseille Page 3 sur 8
 est le déphasage de i(t) par rapport à u(t)
On rappelle que le mot « déphasage » revêt une signification bien particulière en Electrotechnique en raison de la définition
algébrique de la puissance réactive : le déphasage  est le retard de phase de l’intensité du courant i(t) par rapport à la tension
u(t).
i( )
u( ) en
avance
u( ) en
retard
= t
< 0, car i(t) est en avance sur u(t) d’où un retard de phase négatif
> 0, car i(t) est en retard sur u(t) d’où un retard de phase positif
> 0, car i(t) est en retard sur u(t) d’où un retard de phase positif
< 0, car i(t) est en avance sur u(t) d’où un retard de phase négatif
u( )
i( ) en
retard
i( ) en
avance
= t
Référence sur la tension u(t) : u(t) =
tU sin2
i(t) =
tI sin2
Référence sur l’intensité du courant i(t) i(t) =
tI sin2
u(t) =
tU sin2

S.T.S Informatique et Réseaux pour l’Industrie et les Services techniques
Physique appliquée : Réflexions pédagogiques. Thème II version du 27/02/03
Document issu d’un travail collectif dirigé par Joëlle JACQ IA-IPR Académie d’Aix-Marseille Page 4 sur 8
Cas des signaux périodiques non sinusoïdaux :
La signification physique de la notion de valeur moyenne d’un signal ainsi que l’interprétation géométrique de sa
formule de définition sont des prérequis issus du programme des classes antérieures. Elles seront rappelées aux étudiants, et le
professeur complétera leur information en définissant la valeur moyenne d'un signal périodique au moyen d’une intégrale.
Néanmoins, pour les applications, qui resteront limitées à des signaux de forme simple, on privilégiera l’interprétation
géométrique de la formule de définition plutôt que le calcul intégral traditionnel que les étudiants n’ont pas suffisamment
assimilé à ce niveau de formation. En cas de besoin, pour des signaux plus complexes, on utilisera les possibilités de calcul
offertes par certains logiciels.
Propositions didactiques :
Les prérequis sont issus des programmes de première et/ou de terminale technologiques S.T.I : ce thème devrait être
abordé très tôt dans le cursus car il permet de définir le langage propre aux électroniciens et aux automaticiens qui relient la
« différence de phase » à l’argument d’une fonction de transfert : cela sera réinvesti dans les thèmes III et VII.
L’attention des professeurs est attirée sur le fait, qu’actuellement, la représentation complexe d’un signal sinusoïdal ne
peut pas être considérée comme un acquis commun issu du programme des classes antérieures, car cela dépend en effet de la
spécialité de baccalauréat (Cf. ci-dessus la référence des programmes rénovés) : bien qu’elle soit indispensable dans le présent
programme de la S.T.S I.R.I.S, on n’abusera pas de calculs utilisant cette représentation.
Il est à noter que si la représentation de Fresnel peut éventuellement, selon les acquis antérieurs des élèves, constituer
un intermédiaire pour introduire le formalisme complexe, celle-ci n’est plus jamais utilisée durant les deux années de
préparation à ce B.T.S.
Propositions d’activités au laboratoire pour les étudiants (2 séances de 2h) :
T.P n°II.1.a : valeur moyenne.
Les étudiants observeront différents signaux périodiques, le signal sinusoïdal apparaissant comme un cas particulier
(ce qui permettra, au passage, une ré-appropriation des données fondamentales en régime sinusoïdal). Ils mesureront leur valeur
moyenne.
On utilisera un générateur de fonctions réglé pour reproduire les types de signaux correspondant aux réponses des
systèmes étudiés dans le programme : convertisseurs statiques (thème VIII.3) et transmetteurs de signaux numériques
(thème VI). Ces cas sont suffisamment simples pour permettre aux étudiants, à l’occasion d’un exercice, d’opérer le lien entre
mesure et théorie.
Cette séance de TP sera l’occasion de renforcer les connaissances des étudiants sur l’influence de la touche AC-DC
d’un oscilloscope ou d’un multimètre.
T.P n°II.1.b : théorème de superposition.
Le générateur délivre successivement les signaux :
e(t) = Eo
e(t) = e ond
e(t) = Eo + e ond
On relève le signal observé à l’oscilloscope :
en position DC
en position AC
Modéliser l’entrée de l’oscilloscope en utilisant le schéma ci-
contre.
Appliquer le théorème de superposition pour interpréter les
résultats en exploitant ce modèle.
s(t)
e(t)
R
C
i(t)
K

S.T.S Informatique et Réseaux pour l’Industrie et les Services techniques
Physique appliquée : Réflexions pédagogiques. version 5.4 24 février 2003
Document issu d’un travail collectif dirigé par Joëlle JACQ IA-IPR Académie d’Aix-Marseille Page 5 sur 8
II.2. Propriétés fréquentielles du signal.
Eléments d’analyse du programme :
Compte tenu de l’importance de ses applications, ce thème fait partie des fondamentaux du programme. Néanmoins, il
est rappelé que la définition d’une série de Fourier est un problème mathématique et que l’établissement de l’expression
littérale de coefficients de Fourier ne figure pas au programme de Physique appliquée : on admettra les résultats
mathématiques.
Il s’agit d’abord de convaincre les étudiants de la réalité physique de la décomposition d’un signal périodique en
composantes harmoniques. L’objectif fondamental est ensuite de leur faire comprendre l’équivalence de la représentation
fréquentielle et de la représentation temporelle d’un même signal périodique parce que, dans un certain nombre de cas, seule la
représentation fréquentielle permettra d’interpréter les phénomènes : filtrage, échantillonnage, bande de fréquences occupée par
un signal modulé, compatibilité électromagnétique (C.E.M)….
Les étudiants savent déjà que pour définir une grandeur physique par un signal s(t) modélisé par une fonction
sinusoïdale du temps, il suffit de préciser son amplitude Smax ainsi que sa fréquence f (ou sa pulsation ω). On leur fera
remarquer que la représentation graphique de cette grandeur rendant compte de ces informations revêt des formes différentes
qui dépendent du repère adopté. Ainsi, dans la représentation temporelle de la fonction sinusoïdale, on choisit un repère, normé
en s en ordonnées et normé en t en abscisses. Mais si l’on choisit un repère normé en Smax en ordonnées et normé en f en
abscisses, on arrive à une représentation spectrale ou fréquentielle du signal. Ces deux représentations contiennent les mêmes
informations sur le signal. Aux étudiants, souvent déroutés par la représentation spectrale, on fera remarquer qu’elle est
contenue dans certaines expressions qui leur sont pourtant familières : ainsi, lorsqu’un musicien dit que la note « La »
correspond à 440 Hz et lorsqu’un électricien ou un mécanicien disent que l’arbre d’une machine tourne à 1500 tr/min, ils font
de la représentation fréquentielle ou spectrale… sans le savoir.
Pour illustrer ce thème, le professeur utilisera principalement des signaux que l’on peut rencontrer :
- en électronique de puissance (onduleur autonome et hacheur série)
- dans le domaine de la transmission d’informations sous forme numérique.
Propositions didactiques :
Les prérequis sont issus du thème II.1 : il est très important d’aborder ce thème le plus tôt possible dans le cursus, car
on en a besoin tout au long des deux années de préparation au B.T.S.
Il est conseillé de consulter le dossier « Ensemble Fourier » sur le CD ROM « Repères pour la formation » du B.T.S
I.R.I.S et sur le site WEB du rectorat de l’académie d’Aix-Marseille : ce dossier contient un diaporama et des outils de
simulation utilisant un tableur.
Exemple de chronologie de présentation du thème II.2.
En l’absence de support mathématique (théorie des séries de Fourier), la notion de filtrage est très utile pour
introduire expérimentalement l’analyse fréquentielle. Mais la logique voudrait que l’on aborde le filtrage en
s’appuyant sur les représentation spectrales… Fort heureusement, le mot filtre a la même signification dans le langage
scientifique de l’électronicien et dans le langage courant.
Rappel des limites du programme :
Ni la définition mathématique d’une série de Fourier,
ni l’établissement de l’expression littérale de coefficients de Fourier
ne font partie du programme de physique appliquée.