Word 2007

TP3
À
À l la a d dé éc co ou uv ve er rt te e d de e l la a d di if ff fr ra ac ct ti io on n
Objectifs de la séance :
- Étudier le phénomène de diffraction ;
- Étudier ou utiliser le phénomène de diffraction dans le cas des ondes lumineuses.
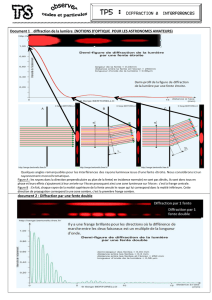
À marée basse, le port de San
Sébatiàn, au Pays Basque espagnol, est
témoin d’un phénomène naturel : la
diffraction des ondes à la surface de
l’eau. Les vagues crées par la houle
subissent un phénomène de
diffraction au passage des rochers
proches du littoral.
1. Le rayon lumineux
Afin de chercher à isoler un rayon de lumière laser, on
fait passer un faisceau de lumière laser à travers une
fente réglable (ci-contre), que l’on envoie sur un écran.
Vérification expérimentale :
Protocole expérimental :
 Placer, sur le banc d’optique, la fente à quelques centimètres du LASER et un écran à une distance D = 1,50 m ;
 Réduire progressivement l’ouverture de la fente ou bien utiliser des fentes d’ouverture différentes ;
 Observer les figures obtenues sur l’écran pour différentes ouvertures.
 Schématiser et légender cette figure en utilisant le vocabulaire suivant : tache centrale, taches secondaires,
extinction.
Q
Q1 1. . Que devrait-on observer sur l’écran ?
Q
Q2 2. . Que va-t-on observer au fur et à mesure que la largeur de la fente diminue ?
Questions

2. Diffraction de la lumière par un fil
Le physicien français Jacques BABINET (1794 – 1872) énonce un principe affirmant que la figure de diffraction
obtenue par un fil tendu est la même que pour une fente de même épaisseur.
 Proposer un protocole expérimental permettant de vérifier ce principe.
Ce protocole expérimental doit présenter la façon dont on va utiliser le matériel ainsi que les mesures à effectuer
pour vérifier ce principe.
3. Étude théorique de la diffraction
Nous avons vu dans la première partie que plusieurs paramètres peuvent influer sur la figure de diffraction. En
particulier la longueur d’onde  de la source de lumière laser et la largeur a de la fente.
 Proposer un protocole expérimental rigoureux permettant de montrer l’influence sur la figure de diffraction
de ces deux paramètres : la longueur d’onde du laser  et la largeur de la fente (ou l’épaisseur du fil) a. Le protocole
mettra en jeu 3 mesures pour chaque caractéristique à vérifier.
Exploitation :
La grandeur permettant de décrire une figure de diffraction (ci-dessous) est l’angle θ (exprimé en radian), qui
correspond à l’écart angulaire entre le milieu de la tache centrale et la première extinction (voir schéma ci-dessous).
Q
Q3 3. . En déduire un lien entre la figure obtenue sur l’écran et la largeur a de la fente ?
Q
Q4 4. . Peut-on isoler un rayon lumineux ? Justifiez votre réponse.
Q
Q5 5. . Quel(s) autre(s) paramètre(s) peut(vent) influer sur la figure obtenue ?
Questions

L = largeur de la tache centrale
D = distance entre l’objet diffractant (fil ou fente) et l’écran
4. Application
En vous inspirant des expériences et des résultats précédents, proposer un protocole expérimental pour mesurer le
diamètre de l’un de vos cheveux. Mettre en œuvre ce protocole.
C
CO OR RR RE EC CT TI IO ON N
1. Le rayon lumineux
Q
Q1 1. .
(0,5 pt)
Q
Q2 2. .
(0,5 pt)
On observe sur l’écran une tache centrale brillante et des taches plus petites et moins intenses autour réparties
symétriquement.
La figure de diffraction s’étale perpendiculairement à la direction de la fente : (2 pts)
Q
Q3 3. .
Plus la fente est étroite, plus la figure de diffraction s’étale. (1 pt)
Q
Q4 4. .
Non, on ne peut pas isoler un rayon de lumière car plus on restreint le faisceau laser et plus la lumière s’étale. Le
rayon de lumière reste le modèle de propagation rectiligne de la lumière et n’a aucune réalité physique. (1,5 pt)
Q
Q6 6. . Dans l’approximation des angles petits (tan θ ≈ θ), établir la relation entre θ, L et D.
Q
Q7 7. . D’après les résultats précédents, indiquer quelle est la relation entre θ, λ et a parmi les propositions :
 θ = λ × a  θ =
λ
a
 θ =
a
λ
Q
Q8 8. . À partir de mesures expérimentales (protocole à élaborer) vérifier la relation choisie en traçant une courbe
judicieusement choisie à l’aide d’un tableur-grapheur.
Questions
Objectifs de la séance : (0,5 pt)

Q
Q5 5. .
La longueur d’onde , la distance objet fente-écran D et la largeur de la fente a peuvent influencer la largeur de
la tache de diffraction L. (1 pt)
2. Diffraction de la lumière par un fil
Protocole expérimental :
Il suffit de réaliser le montage précédent en remplaçant la fente par un fil tendu et d’observer la figure de
diffraction. (2 pts)
3. Étude théorique de la diffraction
Il faut réaliser le montage expérimental utilisé dans les expériences précédentes puis faire varier le paramètre étudié
(longueur d’onde du laser  et largeur de la fente). On observe alors les modifications qui s’en suivent sur la figure
de diffraction. Trois mesures seront effectuées pour l’étude de chaque paramètre. (2,5 pts)
On constate expérimentalement que :
- Si  augmente, L augmente ;
- Si D augmente, L augmente ;
- Si a augmente, L diminue.
Q
Q6 6. .
On a  ≈ tan  =
L2
D
=
L
2D
. (1 pt)
Q
Q7 7. .
D’après les observations ci-dessus, on en déduit que la relation entre θ, λ et a est :
θ = λ × a θ =
λ
a
θ =
a
λ
(0,5 pt)
Q
Q8 8. .
Il suffit de faire des mesures de L (puis on calcule ) en fonction de l’ouverture de la fente puis on trace  =
f(1/a) pour chaque longueur d’onde testée :
 On obtient des droites qui passent par l’origine :  est bien inversement proportionnel à a.
Les modélisations des droites donnent les équations suivantes :
θv =
-9
532 10
a
et θr =
-9
632,8 10
a
Les valeurs des coefficients directeurs des droites correspondent aux valeurs des longueurs d’ondes des lasers
utilisés :
 Laser rouge λr = 632,8 nm
 Laser rouge de poche (Jeulin) λr = 650 nm
 Laser vert λv = 532 nm
(1 pt)
(3 pts)
(1 pt)

4. Application
Pour D = 1,50 m, on place un cheveu à la place des fils calibrés. On mesure la longueur L de la tache centrale de
diffraction, puis on calcule la valeur de  dans l’approximation des petits angles. On reporte cette valeur sur la
courbe, puis on lit l’abscisse correspondante qui nous donne la valeur de l’épaisseur du cheveu. (2 pts)
MATÉRIEL MIS À DISPOSITION :
 Un ordinateur muni du logiciel d'acquisition de données/tableur-grapheur LatisPro.
 Une règle métallique.
 Un banc d’optique avec un porte lentille et un écran
 Cinq postes sont munis d’un laser He-Ne, deux postes sont munis d’un laser He-Ne sur support
 Un jeton muni entre autre de3 fentes de largeur 40, 70 et 120 μm et de 3 trous de diffraction de diamètre
40, 70 et 120 μm