118 ko

1
TS2 Elt
ETUDE D’UNE VOITURE ELECTRIQUE
La voiture est entraînée par une machine à courant continu associée à un hacheur quatre
quadrants.
Le problème est constitué de trois parties indépendantes :
— étude du motovariateur fonctionnant en traction,
— étude du freinage de la voiture,
— étude du chargeur de batteries.
I Fonctionnement du motovariateur
La machine à courant continu (MCC) à flux constant , parfaitement compensée, possède les
caractéristiques suivantes :
— résistance d’induit négligeable ;
— pour le fonctionnement nominal : Inom = 90A, Unom = 260V et nnom =1 500trmn-1 ;
— les pertes fer et mécaniques sont négligées.
1. Fonctionnement en régime nominal
1.1. On rappelle que la force électromotrice (f.e.m.) E est proportionnelle à la vitesse
angulaire Ω : E = KΩ. Calculer K en V.s.rad-1.
1.2. Démontrer que Te, le moment du couple électromagnétique est proportionnel au
courant d’induit I.
1.3. Calculer Tnom le moment du couple électromagnétique nominal.
2. Le fonctionnement en moteur
La voiture roule à vitesse constante sur une route plane. Le moment du couple opposé à la
machine à courant continu est constant.
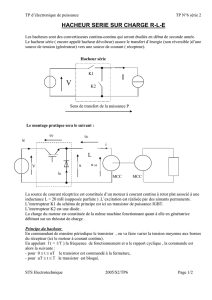
Le pont est formé de quatre interrupteurs électroniques constitués d’un transistor IGBT
associé à une diode placée en anti-parallèle.
Figure 1
D2
H3
uC
iC
E
Uc
R
L
D1
H4
H1
D4
H2
D3
Batterie

2
Les composants électroniques sont considérés parfaits :
— à l’état passant, les IGBT et les diodes seront assimilés à des interrupteurs fermés,
— à l’état bloqué, ils seront assimilés à des interrupteurs ouverts.
Les transistors sont commandés à la fréquence de 10kHz de la façon suivante :
— de 0 à αT : les interrupteurs 1 et 4 sont fermés ;
— de αT à T les interrupteurs 2 et 3 sont fermés.
On règle α =0,8.
2.1. Tracer l’allure de la tension u(t) aux bornes de la machine. Préciser l’amplitude et la
période de u(t).
2.2. Etablir l’expression de la valeur moyenne de la tension u(t) : <u> = Uc (2α – 1).
2.3. En déduire la fréquence de rotation de l’induit en tr.min-1.
2.4. L’allure du courant est tracée sur le document réponse 1. Indiquer sur ce document les
composants du hacheur assurant la conduction du courant (D1, T1, D2,…).Ecrire
l’équation différentielle liant u(t) à i(t), L et E.
2.5. Justifier l’égalité entre la valeur moyenne <u> et la f.e.m.E.
2.6. Justifier la représentation de intensité i(t) du courant dans l’intervalle de temps
compris entre 0 et αT.
2.7. Justifier la représentation de intensité i(t) du courant dans l’intervalle de temps
compris entre αT et T.
2.8. Etablir l’expression de l’ondulation du courant Δi = (IMax – Imin) =
α1
L
U2 c
αT.
2.9. A partir du graphe de i(t) calculer l’inductance L de l’induit.
II Etude du freinage électrique de la voiture
La voiture roule en descente à vitesse constante, le moment du couple exercé sur l’arbre du
moteur devient négatif : T = –120 Nm et n = 900 tr.min-1
1. Calcul des grandeurs.
1.1. Calculer les valeurs moyennes <u> de la tension u(t) et <i> de l’intensité i(t) du
courant d’induit. On rappelle que la résistance de l’induit est négligeable.
1.2. Déterminer le rapport cyclique α permettant d’obtenir cette valeur moyenne de la
tension.
1.3. L’allure du courant est tracée sur le document réponse 2. Indiquer sur ce document
les composants du hacheur assurant la conduction du courant (D1, T1, D2,…).
1.4. Calculer la puissance active P reçue par la machine en considérant que l’intensité du
courant d’induit est constante. Justifier le signe négatif de cette puissance.
2. Etude du module de dissipation.
En cas de freinage de la voiture, l’énergie est convertie sous forme électrique par la MCC qui
la restitue par l’intermédiaire du hacheur aux batteries d’accumulateurs. Toutefois, l’intensité
du courant de charge des batteries étant limité, il est nécessaire d’utiliser un module de
dissipation si cette intensité devient trop importante. Ce module est étudié dans la partie
suivante.

3
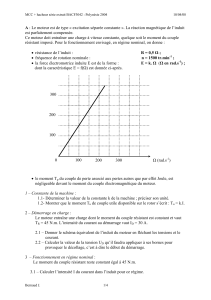
La figure 2 représente le module placé aux bornes du condensateur
Figure 2
Pour simplifier, le hacheur est remplacé par une source débitant un courant constant
d’intensité Is = – <i> = 40A.
Le module de dissipation permet de décharger le condensateur lorsque la tension aux bornes
de celui-ci devient trop importante. Le transistor K est commandé en fonction de la tension uc
aux bornes du condensateur.
Le graphe de la tension uc(t) est représenté sur le document réponse 3 ainsi que le cycle de
fonctionnement.
2.1. Analyse de uc(t) :
2.1.1. A partir du graphe de la tension uc(t), donner les valeurs des deux seuils du
comparateur à hystérésis Umin et UMax .
2.1.2. Toujours à l’aide du graphe de uc, orienter le cycle du document réponse 3 en
plaçant les flèches correspondant aux déplacements du point de
fonctionnement.
2.2. Calcul de la capacité du condensateur :
2.2.1. Donner la relation qui lie ic(t), ip(t) et Is. Que vaut ip(t) lorsque le transistor Tp
est bloqué ? Que vaut alors ic(t) ?
2.2.2. Pour t compris entre 0 et t1, le transistor Tp est bloqué : donner l’équation
différentielle liant uc à Is et à C.
2.2.3. Justifier le fait que uc(t) est une droite.
2.2.4. Calculer sa pente, en déduire la capacité du condensateur.
2.3. Etude des courants :
2.3.1. La puissance restituée par le hacheur est de 11,3kW. Calculer la valeur efficace
de l’intensité du courant traversant la résistance Rp de 5Ω.
2.3.2. Entre t1 et t2, le transistor Tp est passant.
— Calculer la pente de uc(t) et en déduire la valeur de ic(t) sur cet intervalle.
— Montrer que ip(t) = 58 A.
2.3.3. Tracer, sur le document réponse 2, les graphes des intensités ip(t) et ic(t) des
courants.
Préciser les valeurs significatives de ces intensités.
Is
Ip
Rp
Hacheur 4Q
C
Dp
uC
iC
Tp
Trigger ou
comparateur à 2
seuils
M

4
3. Comparaison des durées de freinage.
La MCC tourne à 900 trmn-1 ; le couple de charge est constant et vaut : Tch = 40Nm.
Le moment d’inertie de la charge et du moteur est J = 4kg.m2.
3.1. En t =0, on ouvre l’induit : le moteur n’est pas alimenté.
3.1.1. Donner l’expression du moment du couple d’accélération J
dt
d
en fonction de
Tch . Tracer l’allure de la courbe de ralentissement Ω(t).
3.1.2. Calculer la durée d’arrêt de l’induit.
3.2. Le hacheur fonctionne en récupération : l’intensité du courant d’induit est constante et
vaut <i> = – 73A.
3.2.1. Calculer Te le moment du couple électromagnétique. Interpréter son signe.
3.2.2. Donner l’expression du moment du couple d’accélération J
dt
d
en fonction de
Tch et Te. Tracer l’allure de la courbe de ralentissement Ω(t).
3.2.3. Calculer la nouvelle durée d’arrêt de l’induit.

5
I 2.4
II 1.3
48
49
50
i en A
0
10
t en μs
αT
T
DOCUMENT REPONSE 1
– 73
– 72
0
10
t en μs
αT
T
Intervalles de conduction
Intervalles de conduction