Document élève.

1/2
3L
L/2
L/2
L
θ
θ
D
L
TS TP Physique 4 - PROPRIETES DES ONDES
I. DIFFRACTION DES ONDES LUMINEUSES
On utilisera le phénomène de diffraction des ondes lumineuses pour déterminer la dimension d'une ouverture inconnue.
1. Principe
Pour mesurer l'épaisseur d'un cheveu ou d'une fente, on peut utiliser le phénomène de diffraction.
Le physicien français Jacques Babinet (1794-1872) énonce un principe affirmant que la figure de diffraction obtenue par un fil
tendu est la même que pour une fente de même épaisseur. Le lien qui existe entre la figure de diffraction et l'épaisseur d'un fil
tendu va ainsi permettre de déterminer le diamètre d'un cheveu.
2. Matériel (4 groupes)
3. Manipulation (Compétence évaluée : Réaliser)
! Attention, ne pas regarder directement dans le faisceau du laser !
 Placer l'émetteur laser en face du support de fente, à environ 10 cm sur un axe commun. La diapositive doit être
perpendiculaire à l'axe : utiliser la fente la plus grosse pour commencer.
 Puis placer l'écran à 1,60 m devant la fente (cette distance doit rester constante pendant la manipulation).
 Placer une feuille de papier A4 sur l'écran, puis marquer les « bords »
(en fait le milieu de chaque zone d’extinction) de la tache centrale
au crayon, ainsi que les bords des 2 ou 3 taches lumineuses de
chaque coté.
 Refaire la même manipulation pour toutes les fentes.
4. Exploitation (Compétence évaluée : Analyser)
Rédiger un rapport sur un feuille annexe, en répondant aux questions.
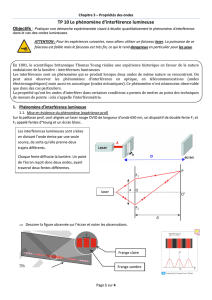
a) Pour chaque fente, mesurer la largeur moyenne L de la tache centrale, en mm,
en utilisant 1, 3, 5, ou 7 taches lumineuses comme indiqué sur le schéma ci-
contre. Placer les résultats dans le tableau suivant :
a : largeur de la fente (en mm) et L : largeur moyenne de la tache lumineuse centrale(en mm).
Fente n°
1
2
3
4
5
6
7
a(mm)
0,40
0,28
0,12
0,10
0,050
0,040
?
L(mm)
1/a( )
b) Tracer le graphe L = f (1/a) en utilisant le quadrillage page 4/4
c) Quelle est la nature de la relation entre L et 1/a ?
(Linéaire, affine, sinusoïdale, parabolique ...)
d) En déduire la valeur du coefficient directeur, qui lie L et 1/a.
k =
e) Donner l'expression littérale liant la tangente du demi angle au sommet θ de la tache lumineuse centrale à la largeur L et à
la distance (Fente – Ecran) D.
f) Quand un angle est petit (inférieur à 5 °), la tangente de l’angle est égale à la valeur de l’angle exprimé en radians. En
déduire l'expression littérale de θrad .
g) Sachant θrad = λ / a , calculer la longueur d'onde λ de la lumière rouge créée par le laser.
Comparer avec la valeur indiquée par le constructeur du laser λ = 650nm . (Compétence évaluée : Valider)
 feuille de papier A4
 1 banc d'optique (nouveau)
 1 support source
 1 Emetteur laser
 1 diapositive comportant 7 fentes sur 1
support
 1 Ecran rigide sur support
Laser
Fente
Ecran

2/2
II. INTERFERENCES LUMINEUSES
Principe
Du fait de la très grande sensibilité des figures d'interférences aux
conditions expérimentales, les mesures par interférences, ou interférométrie,
se sont répandues dans de nombreux secteurs, comme dans l'industrie, pour
la mesure de très faibles variations d'épaisseur. En astronomie, on s'arrange
pour observer la même source en deux endroits à l'aide de deux télescopes et
l'on fait interférer les deux images. L'évolution de la figure d'interférences
obtenue en fonction de l'écartement des télescopes permet de remonter aux
dimensions de la source observée. On va ici modéliser les deux télescopes
par deux fentes.
L'analyse de la figure d'interférences permet de déterminer l'espacement
entre les deux fentes.
Mise en œuvre ou laboratoire, Matériel
bifente
banc optique gradué
diode laser.
baguette en verre
écran gradué
tableur-grapheur
(Compétence évaluée : Réaliser)
Réaliser, sur le banc optique gradué, le montage des bifentes de Young
Questions : (Compétence évaluée : Analyser)
1. Qu'appelle-t-on interférences ?
La baguette en verre est utilisée ici pour étendre le faisceau laser.
2. Dessiner la figure obtenue sur l'écran et noter les observations.
3. Que peut-on dire sur les deux ondes lumineuses issues des fentes en
un point d'une zone brillante ? D'une zone sombre ?
4. Recenser les paramètres expérimentaux susceptibles d'influencer la figure d'interférences obtenue.
Mesures et exploitation (Compétence évaluée : Analyser)
La figure d'interférences est caractérisée par l'interfrange, noté i, qui est la distance
séparant deux franges brillantes
(Ou deux franges sombres) consécutives sur l'écran voir figure ci-contre. Pour augmenter
la précision des mesures, on effectuera la moyenne sur l'ensemble des interfranges de la
figure.
5. Pour différentes valeurs de D, entre I et 2 m environ, mesurer l'interfrange i sur l'écran :
6. À l'aide de l'animation "interférences " consultable sur le site www.bordas.espace.fr/lycee, et en traçant des courbes
Judicieusement choisies, préciser comment évolue la valeur de l'interfrange :
a. avec la valeur de l'espacement l entre les fentes :
b. avec la valeur de la longueur d'onde  :
7. Déduire des résultats précédents l'expression correcte de l'interfrange i dans le cas de l'expérience des bifentes de Young :
a. i= l /D; b. i = dl c. i= l /D; d. i= l /D/ l ;
8. a. Tracer la courbe D = f(i) ou l’imprimer.
b. En déduire la distance l entre les deux fentes :
c. Comparer cette valeur à celle fournie par le constructeur en calculant l'écart relatif, puis conclure.
Pour conclure
9. Quels paramètres ont une influence sur la figure d'interférences ?
10. En interférométrie, on utilise souvent des filtres ne laissant passer qu'une longueur d'onde pour faciliter l'étude des
interférences. Proposer une explication.