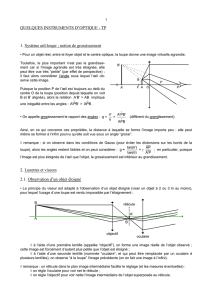
De la loupe à l`oculaire

FICHE T.P. 02 De la loupe à l’oculaire …
Une des difficultés dans l’étude des instruments d’optique est le rôle de l’oculaire (élément commun à tous les instruments
d’optique étudiés par la suite).
Pour une observation sans fatigue pour l’œil, il faut regarder à l’infini.
Un oculaire est une lentille convergente utilisée en loupe, dans le cas particulier où l’image est à l’infini.
Se pose alors le problème suivant :
dans le cas de la loupe :
L’image est plus grande que l’objet (c’est visible sur le schéma).
Par contre dans le cas de l’oculaire :
On ne peut comparer les dimensions respectives de l’objet et de l’image (celle ci étant à l’infini).
Comment admettre que l’image paraît plus « grosse » pour l’observateur ?!
II. Une bille plus grande, paraît-elle nécessairement plus grosse ?
Rappel de la notion de diamètre apparent (qui a déjà été vue au début du programme de seconde).
Ce que l’on perçoit d’un objet dépend, bien sûr, de sa taille, mais aussi de la distance à laquelle il se trouve de l’observateur.
On peut aligner les deux objets de sorte que le plus petit (plus près de l’observateur) masque le plus grand : preuve qu’il
paraît plus gros.
Pour distinguer les détails d’un objet, la première chose à faire consiste à approcher l’objet de l’œil. On augmente ainsi le
diamètre apparent de l’objet, c’est à dire, l’angle (exprimé en rad) sous lequel est vu l’objet. (comparer les schémas n°1 et
n°2).
III. « Grossir » avec une lentille convergente : la loupe.
Ce paragraphe a pour but d’introduire la notion de grossissement.
La loupe grossit car elle permet d’augmenter l’angle sous lequel est vu l’objet.

Grossir : c’est augmenter le diamètre apparent.
Quand l’objet est à environ 25 cm (distance minimale de vision distincte, notée dm, pour un œil normal, sans loucher !), pour
augmenter encore le diamètre apparent on utilise une loupe. (comparer les schémas n°2 et n°3).
Le grossissement de la loupe est défini par :
'
G
’ : angle sous lequel on voit l’image.
 : angle sous lequel on voit l’objet.
Pour simplifier, plaçons l’œil de l’observateur sur le foyer F’ de la lentille.
tan  =
m
d
AB
.
tan’  ’ =
'OF
AB
.
'
G
=
'OF
dm
. Avec dm = 0,25 m pour un œil normal.
Le grossissement de la loupe pour un œil normal placé au foyer F’ vaut alors :
'4 1 OF
G
=
4
1
V
On peut faire constater aux élèves que grossir 10 fois, par exemple, c’est augmenter 10 fois le diamètre apparent, soit diviser
par 10 la distance d’observation.
Pour voir les détails d’un petit objet on peut l’approcher à 25 cm de l’œil.
Quand on observe l’image de cet objet à travers une loupe qui grossit 10 fois, on voit ce que l’on verrait de l’objet si notre
oeil nous permettait de le voir nettement à une distance de 2,5 cm.
Ne pas confondre grandissement et grossissement !!!
 La question qui se pose est : « quand on forme , avec une lentille convergente, une image virtuelle de plus
en plus grande, est-elle de plus en plus grosse ? ».
Tout dépend de la position de l’œil :
Si l’œil est placé en G (schéma ci-dessous), quand l’image grandit, l’angle sous lequel elle est vue diminue .  augmente
alors que G diminue.
Si l’œil est placé en H (schéma ci-dessous), quand l’image grandit, l’angle sous lequel elle est vue aussi.
Si l’œil est placé sur F’ (schéma ci-dessous), QUELLE QUE SOIT LA POSITION DE L’OBJET l’angle sous lequel est vu
l’image vaut |’| =
'OF
AB
. C’est donc ce cas qui est proposé aux élèves.
 Dans le cas ou l’image se trouve à l’infini (cas de l’oculaire), le problème ne se pose plus puisque
QUELLE QUE SOIT LA POSITION DE L’ŒIL, l’angle sous lequel est vu l’image vaut |’| =
'OF
AB
.

IV. L’oculaire des instruments d’optique.
1. Observer sans fatigue pour l’œil …
Pour voir nettement un objet proche, l’œil doit faire « une mise au point » : on dit qu’il doit accommoder. Ceci nécessite
l’action de muscles de l’œil. Cette accommodation n’intervient pas dans le cas d’une observation « au loin ».
On pourrait dire : un œil normal, au repos, est conçu pour voir nettement les objets au loin.
L’image formée par un instrument optique devra se trouver à l’infini car cela correspond à une observation sans fatigue pour
l’œil.
2. De la loupe à l’oculaire :
Les élèves disposent de deux lentilles convergentes : V1 = 20  et V2 = 5 .
Ils déterminent expérimentalement leur distance focale (cf TP 01).
Ils constatent que la loupe de 20  grossit plus.
Schématiser les deux expériences sur un schéma à l’échelle.
L’image étant à l’infini, quelle que soit la position de l’œil on a G = V/4.
G1 = V1/4 = 5.
G2 = V2/4 = 1,25.
Un oculaire grossit d’autant plus que sa vergence est grande (distance focale petite).
Pour avoir un grossissement supérieur à 1, il faut que l’oculaire ait une vergence V > 4 soit une focale OF’ < 25 cm.
Rque : dans la modélisation des instruments optique, il nous semble préférable de modéliser les oculaires par des lentilles de
focales inférieures à 25 cm plutôt que des lentilles de 30 cm comme dans beaucoup de livres.

L’oculaire (lentille placée du coté de l’œil) des instruments d’optique que nous étudierons, est une lentille convergente
« utilisée en loupe » dans le cas où l’objet est placé sur F car, dans ce cas, l’image est à l’infini, ce qui permet une
observation sans fatigue pour l’œil.
V. « Grossir » avec deux lentilles convergentes : introduction au microscope.
On peut rappeler que l’oculaire est la lentille située du coté de l’œil.
Comment utiliser une deuxième lentille, placée entre l’objet et l’oculaire, pour augmenter encore le diamètre apparent.
A ce stade de leur apprentissage, les élèves ont tous les éléments pour comprendre le principe de fonctionnement du
microscope. Le but de ce paragraphe est d’introduire, par une discussion avec la classe, le TP04.
Après ce TP, on peut s’attendre à ce qu’ils proposent d’observer l’objet à la loupe. Puis d’observer l’image obtenue à la
loupe (l’oculaire).
La première lentille grossit une première fois. On obtient une image plus grande que l’objet. L’oculaire, lui, grossit cette
image.
En utilisant le simulateur, pour expliquer le rôle de l’objectif, l’enseignant rappelle que pour que l’image intermédiaire soit
la plus grande possible l’objet doit se trouver au voisinage de F (foyer de l’objectif).
Deux cas possibles :
 Celui proposé (sans doute) par les élèves : observation de AB à la loupe, présente l’inconvénient de
renvoyer l’image intermédiaire A’B’ (virtuelle), « à gauche » de la lentille, et ce d’autant plus loin qu’elle est grande. Cela
posera donc un problème pour placer cette image intermédiaire au foyer de l’oculaire qui est, on l’a vu, une lentille de petite
distance focale.
 L’autre possibilité est d’utiliser la première lentille pour obtenir une image intermédiaire agrandie et « à
droite » de la lentille. Cette image est ensuite observée à la loupe.
Les élèves réalisent l’expérience.
Ils récupèrent l’image agrandie de l’objet sur un écran, puis observent cette image à la loupe.
L’étude détaillée du microscope est traitée au TP04.
Pour la séance suivante (TP03), revoir les notions vues en 1°S sur les miroirs plans.

FICHE T.P. 02 De la loupe à l’oculaire …
Liste du matériel.
5 groupes
 2 billes de tailles différentes.
Pour le III.
 L1 : V1 = 20 
 L2 : V2 = 5 
 Un banc optique et ses accessoires.
 Un objet de petite taille : remplacer le F traditionnel par celui
ci-joint (distance interligne 1 mm ; épaisseur du trait  0,1 mm)).
L’imprimer sur un transparent spécial imprimante.
Superposer le transparent à du papier calque pour une meilleure diffusion.
Pour le IV.
 Le logiciel de figures d’optique animées.
 L1 : V1 = 20  servira d’objectif.
 L3 : V3 = 10  servira d’oculaire.