AQUISAV - Evaluation

A
Aq qu ui is sa av v - - D DO OC CU UM ME EN NT TA AT TI IO ON N
17-avr.-17 - Page 1 sur 7
Métier : CULTURE GÉNÉRALE
Domaine de compétences : SCI- Géométrie dans le plan
Code : COM-2011-012039
Intitulé de la compétence : IDENTIFIER ET CONSTRUIRE LES SYMETRIES
« Studio Dessin : récupérer la photo en ligne sur Aquisav »
S
SO OM MM MA AI IR RE E
1) INTRODUCTION
2) SYMETRIE AXIALE
3) SYMETRIE CENTRALE

A
Aq qu ui is sa av v - - D DO OC CU UM ME EN NT TA AT TI IO ON N
17-avr.-17 - Page 2 sur 7
C
CO OU UR RS S
I- INTRODUCTION
L’ébéniste, le tailleur de pierre, le sellier et bien d’autres encore utilisent la symétrie pour
élaborer des ouvrages formés de deux parties parfaitement identiques disposées en miroir par
rapport à un axe matérialisé ou non. Dans ce cas, ils utilisent la symétrie axiale.
Une autre symétrie existe : c’est la symétrie centrale dans laquelle une figure tourne autour
d’un point d’un demi-tour. Cette symétrie est beaucoup moins utilisée dans les métiers de
l’artisanat.
II- SYMETRIE AXIALE
Et oui, même la nature semble apprécier la symétrie !
Ce magnifique papillon déploie ses ailes sur lesquelles aucune tache ne manque pour créer une
belle symétrie.
Sur le croquis des maisons qui se font face, si on plie la feuille sur la droite qui les sépare, les
deux maisons seront parfaitement superposées.
1) Définition d’une symétrie d’un point
Soit une droite (D), le symétrique du point A par rapport
à cette droite est le point A’ tel que la droite (D) est la
médiatrice du segment
D
Do on nc c, , p po ou ur r c co on ns st tr ru ui ir re e l le e s sy ym mé ét tr ri iq qu ue e d d’ ’u un ne e f fi ig gu ur re e q qu ue el lc co on nq qu ue e, , o on n p pr ro oc cè èd de e p po oi in nt t p pa ar r p po oi in nt t. .

A
Aq qu ui is sa av v - - D DO OC CU UM ME EN NT TA AT TI IO ON N
17-avr.-17 - Page 3 sur 7
E
Ex xe em mp pl le e
C
Co on ns st tr ru ui ir re e l le e s sy ym mé ét tr ri iq qu ue e d du u p po ol ly yg go on ne e A AB BC CD DE E p pa ar r r ra ap pp po or rt t à à l l’ ’a ax xe e d de e s sy ym mé ét tr ri ie e d do on nn né é. .
M
Mé ét th ho od de e : : O On n c co on ns st tr ru ui it t l le es s p po oi in nt ts s A A’ ’, , B B’ ’, , C C’ ’, , D D’ ’ e et t E E’ ’ s sy ym mé ét tr ri iq qu ue es s d de es s p po oi in nt ts s A A, , B B, , C C, , D D e et t E E p pu ui is s
o
on n r re el li ie e l le es s p po oi in nt ts s d da an ns s c ce et t o or rd dr re e p pa ar r d de es s s se eg gm me en nt ts s d de e d dr ro oi it te e. .
2) Propriétés
On constate que :
- L’image d’un segment est un segment de même longueur
- L’image d’un angle est un angle de même mesure
- L’image d’un cercle de centre A est un cercle de même rayon et de centre A’ image de A.
- La symétrie axiale conserve le parallélisme
D’après l’exemple ci-dessous, les symétriques des deux droites (EH) et (IJ) parallèles sont des
droites parallèles (E’H’) et (I’J’).
- La symétrie axiale conserve les angles car :
D’après l’exemple ci-dessous, les symétriques des deux droites perpendiculaires (EH) et (KL)
sont des deux droites (E’H’) et (K’L’) perpendiculaires.

A
Aq qu ui is sa av v - - D DO OC CU UM ME EN NT TA AT TI IO ON N
17-avr.-17 - Page 4 sur 7
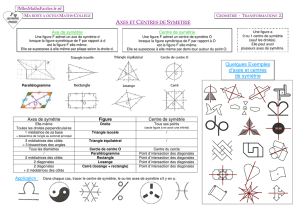
3) Axes de symétrie des figures courantes
Le carré, le rectangle, le losange, le cercle, les triangles isocèles et équilatéraux possèdent des
axes de symétrie remarquables.
 Le carré :
Le carré a 4 axes de symétrie :
Les diagonales (en rouge)
Les médiatrices (en vert) des côtés.
 Le rectangle
Le rectangle n’a que deux axes de symétrie :
Les médiatrices des côtés.

A
Aq qu ui is sa av v - - D DO OC CU UM ME EN NT TA AT TI IO ON N
17-avr.-17 - Page 5 sur 7
 Le Losange
Le losange a deux axes de symétrie :
Les diagonales.
 Le cercle
Le cercle a une infinité d’axes de symétrie :
Les diamètres
 Le triangle isocèle
Le triangle isocèle n’a qu’un axe de symétrie
qui est à la fois hauteur, médiane, médiatrice de la base
et bissectrice de l’angle au sommet.
 Le triangle équilatéral
Le triangle équilatéral a 3 axes de symétrie
qui sont à la fois les hauteurs, les médianes,
les médiatrices des côtés et
les bissectrices des angles.
III- SYMETRIE CENTRALE