C4_triphase

1
Chapitre 4
REGIME TRIPHASE EQUILIBRE
x
0,01 0,02 0,03
-300
-200
-100
0
100
200
300

2
I. Définitions
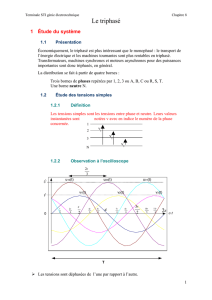
Trois grandeurs alternatives sinusoïdales de même fréquence, même valeur efficace et déphasées
entre elles de
3
2
forment un système triphasé équilibré direct ou inverse.
Exemple :
)tcos(2V)t(v1
,
)
3
2
tcos(2V)t(v2
et
)
3
4
tcos(2V)t(v3
forment un système
triphasé équilibré direct de tensions.
)tcos(2I)t(i1
,
)
3
4
tcos(2I)t(i2
et
)
3
2
tcos(2I)t(i3
forment un système triphasé
équilibré indirect de courants.
1) Représentation de Fresnel
Système direct :
Propriété importante :
- la somme de trois grandeurs formant un système triphasé équilibré est
nulle :
0VVV 321
ou v1(t)+v2(t)+v3(t)=0
2) Représentation complexe
1
1V)t(v 
3
2
j
12
2eVV)t(v 
3
4
j
13
3eVV)t(v 
En utilisant l’opérateur
3
2
j
ea 
on obtient :
11 VV 
,
1
2
2VaV 
et
13 VaV 
soit le trio (1, a², a)
pour un système triphasé équilibré direct et le trio (1, a, a²) pour un système triphasé équilibré
inverse.
Remarques :
- on vérifie toujours que
0aa1 2
-
1a3
-
21 aa 
2
V
3
V
1
V
1
V
2
V
3
V
3
2
ou
+

3
II. Générateur et ligne triphasée
En associant trois générateurs de tension (ou de courant) formant un système triphasé équilibré en
étoile ou en triangle, on crée un générateur triphasé :
Ligne triphasée :
v1, v2, v3 sont les tensions simples (entre phase et neutre) du réseau
u12=v1-v2, u23=v2-v3, u31=v3-v1 sont les tensions composées (entre phases) du réseau
i1, i2, i3 sont les courants de ligne
iN est le courant circulant dans le conducteur du fil de neutre
Les indices 1,2,3 peuvent aussi être désignés par R,S,T ou U,V,W
iN
i3
i2
i1
v3
v2
v1
u31
u23
u12
1
e3
e2
e1
e3
e2
e1
Dans un couplage en étoile, le potentiel
commun des générateurs définit le neutre
2
3
N
A vide, aucun courant ne circule dans les
branches du triangle car e1 + e2 + e3 = 0
1
2
3
1
2
3
N

4
Construction des tensions composées :
2112 VVU 
,
3223 VVU 
1331 VVU 
Un réseau triphasé est qualifié par la valeur efficace U des tensions composées et la fréquence
électrique f de ces tensions.
Exemple : réseau 400V-50Hz
III. Récepteurs triphasés
Un récepteur triphasé équilibré est formé de trois dipôles identiques (même impédance) couplés
soit en étoile soit en triangle :
1) Couplage en étoile
6
31
U
1
V
3
V
23
U
3
V
2
V
12
U
1
V
2
V
Les tensions composées forment donc aussi un
système triphasé équilibré de tensions tel que :
3VUUUU 312312 
6
)U,V(Angle)U,V(Angle)U,V(Angle 313232121
Soit en utilisant les nombres complexes :
6
j
112 e3VU 
6
j
223 e3VU 
6
j
331 e3VU 
IN
N
V1
V1
I1
Z
Z
Z

5
Propriétés du couplage Y :
- le courant qui traverse chaque dipôle est égal au courant de ligne (valeur efficace I)
- la tension appliquée à chaque dipôle est une tension simple du réseau (valeur efficace
V)
- les trois dipôles étant identiques, les courants i1, i2 et i3 forment un système triphasé
équilibré de courants de somme nulle :
N321 I0III 
(loi des nœuds) le
courant dans le conducteur du neutre est nul lorsque le récepteur est équilibré
- puissance active consommée par le récepteur :
 cosIV3P3PPPP 1321
soit
 cosUI3P
avec
)Z(Arg
=déphasage courant/tension propre au dipôle Z
- de même
 sinUI3Q
et
UI3S
2) Couplage en triangle
On montre facilement : J1=J2=J3=J (valeurs efficaces) et
3JI 
soit
6
j
1
1e3JI 
Propriétés du couplage
:
- le courant qui traverse chaque dipôle est différent du courant de ligne : j1=i1+j3 et
3
I
J
- la tension appliquée à chaque dipôle est une tension composée du réseau (valeur
efficace U).
- dans tous les cas
0III 321 
- puissance consommée par le récepteur :
 cosJU3P3PPPP 1321
soit
 cosUI3P
- de même
 sinUI3Q
et
UI3S
Conclusion :
Quel que soit le couplage du récepteur, les formules de calcul des puissances sont
identiques lorsqu’elles sont exprimées en fonction de U et I :
 cosUI3P
et
 sinUI3Q
6
2
J
3
J
3
J
u12
u12
Z
i1
j1
Z
i2
j2
Z
i3
j3
1
I
1
J