TP Phys 2 : Lumière et couleurs

TP n° : Lumière et couleurs
1. Découvrir la loi de Wien
1.1. Spectre d’un corps incandescent
« L’Erta’Ale est un volcan éthiopien dont le nom en langage afar signifie « la montagne qui fume », signe de son
activité quasi permanente. A cause des conditions climatiques extrêmes du désert du Danakil, l’Erta’Ale n’a été visité
que par peu de voyageurs et volcanologues. Les relevés de température les plus récents proviennent des satellites,
dont la résolution spatiale est faible. En conséquence, des expéditions sur le terrain, dotées d’un pyromètre
mesurant à distance le rayonnement infrarouge émis par la lave, sont irremplaçables. »
D’après le bulletin de la Société de volcanologie Genève, avril 2001.
Document 1 :
Mesure au pyromètre optique de la température
des laves du volcan Erta’Ale (Ethiopie)
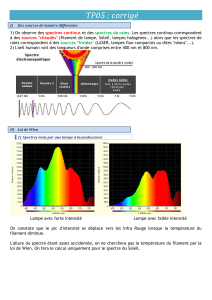
Pour étalonner un pyromètre, des fours (appelés corps noirs) sont utilisés. Le rayonnement émis par ces corps noirs
ne dépend en effet que de leur température absolue, exprimée en kelvin (K) , l’unité de température du système
international : T(K) = T(°C) + 273,15
Document 2 :
Intensité du rayonnement
électromagnétique émis par un
four à différentes températures
T en fonction de la longueur
d’onde dans le vide.
1.2. Exploitation
2.2.1. Rappeler à quel domaine de longueur d’onde dans le vide correspond la lumière visible. Où se situent les
rayonnements UV et IR par rapport à ce domaine.
2.2.2. La température de la lave est comprise entre 600 °C et 1300 °C environ. Expliquer la phrase « le pyromètre
mesure le rayonnement infrarouge émis par la lave ».
2.2.3. Déterminer graphiquement les valeurs λmax correspondant aux longueurs d’onde dans le vide des maxima
d’intensité lumineuse du document précédent.
2.2.4. Rentrer les valeurs de la température T en kelvin et de λmax dans le logiciel Regressi. Représenter la courbe de
λmax en fonction de la température puis en fonction de l’inverse de la température T en kelvin.Quelle est la
courbe la plus simpe a exploiter.Justifier.
Aide : Créer une nouvelle grandeur calculée qui correspond à l’inverse de la température T.
2.2.5. Modéliser la courbe retenue et montrer que son équation est de la forme : λmax = a/T + b où a et b sont des
constantes. Donner les valeurs de a et b et préciser leurs unités.

2. Les lampes à filament arrivent-elles à imiter la lumière du soleil ?
2.1. Loi de Wien
Wilhelm Wien était un physicien allemand, célèbre pour ses travaux sur les lois du rayonnement et de la chaleur. En
étudiant le rayonnement de corps de nombreux objets à différentes températures, Wilhelm Wien a remarqué que la
longueur d’onde correspondante au maximum de rayonnement était inversement proportionnelle à la température
du corps.
Loi de Wien : écrire la loi de Wien avec : T, la température en kelvin ( K )
λ, la longueur d’onde en mètre (m)
σ, le coefficient de proportionnalité (σ = 2,898.10-3 m.K )
2.2. Mesures et exploitation
Un spectromètre permet d’obtenir le profil spectral de la lumière, c’est-à-dire la courbe donnant l’intensité
lumineuse des radiations de la lumière en fonction de la longueur d’onde de ces radiations.
Lumière solaire :
Diriger la fibre optique du spectromètre vers le Soleil et réaliser l’acquisition du profil spectral de la lumière solaire
2.2.1. Déterminer la longueur d’onde λmax de la radiation la plus lumineuse du spectre solaire.
2.2.2. Déterminer, à l’aide de la loi de Wien, la température T de sa surface.
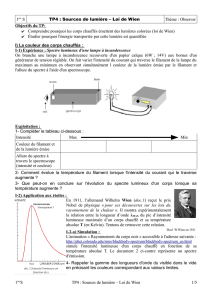
2.3. Lumière émise par un filament chauffé
Placer la fibre optique du spectromètre à proximité de la lampe. Réaliser l’acquisition du profil spectral émis pour
une faible, puis pour une forte température du filament.
2.3.1. Décrire les courbes obtenues et les comparer.
2.3.2. Comparer le profil spectral de la lumière émise par un filament chauffé à celui de la lumière solaire.
2.3.3. Les profils spectraux obtenus avec la lampe permettent-ils de déterminer la température du filament ?
2.3.4. Dans une lampe, le filament de tungstène est porté à une température de 2500°C.
Déterminer à l’aide de la loi de Wien, la longueur d’onde λmax correspondant au pic d’émission lumineuse
du filament de tungstène d’une lampe. Ce pic se situe-t-il dans le visible ?
2.3.5. La température de fusion du tungstène est 3422°C. La lumière émise par une lampe à filament peut-elle
avoir le même profil spectral que la lumière solaire ?
Intensité
λ (.103nm)

Matériel élève : laser, réseau, écran, générateur variable, source de lumière avec miroir, PC ou papier
millimétré.
Matériel professeur : spectrophotomètre, rétroprojecteur,feuilles noires,réseau, filtres colorés.