énoncé

TS spécialité 582674228 page 1
Ph 2.3 INTERPRETATION ONDULATOIRE DES MODES PROPRES
1. REFLEXION D’UNE ONDE SUR UN OBSTACLE:
1.1. Réflexion d’une onde progressive non périodique sur un obstacle:
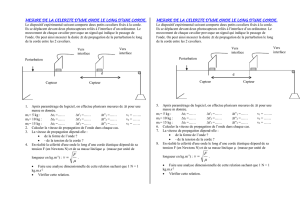
Une corde élastique est attachée à un obstacle fixe.
Une petite perturbation est produite à l’autre extrémité.
Ouvrir le fichier : U/ PHY_CHIM / PC_TS_spe/«ébranlement fixe-libre_reflexion_superposition.xls »
« réflexion d’une onde » et répondre aux questions suivantes :
 Que se passe-t-il au niveau de l’obstacle ?
 Quels sont la direction et le sens de propagation de l’onde réfléchie ? Quelle est sa vitesse ?
 Qu’observe-t-on pour la forme de l’onde réfléchie ?
1.2. Réflexion d’une onde progressive périodique sinusoïdale sur un obstacle:
Ouvrir le fichier : U/ PHY_CHIM puis PC_TS_spe// « Ondes stationnaires.xls »)
Qu’observe-t-on pour l’onde progressive réfléchie :
 Dans le cas d’un obstacle fixe ?
 Dans le cas d’une extrémité libre ?
1.3. Onde stationnaire :
Superposition de 2 ondes progressives non périodiques:
(voir simulation « ondes stationnaires.xls »/ « superposition de 2 ébranlements » ))
Observer le mouvement du point sollicité par 2 ondes se propageant en sens inverse quand les ondes ont :
 la même forme (obstacle libre)
 une forme inversée (obstacle fixe)
Superposition d’une onde progressive périodique sinusoïdale et de l’onde réfléchie :
(voir simulation « Ondes stationnaires.xls »)
Observer la corde soumise à la superposition d’une onde progressive sinusoïdale de fréquence f et de l’onde
réfléchie sur un obstacle fixe :
 quelle est sa forme ?
 L’onde obtenue est-elle progressive ?
 Quelle est l’influence de la fréquence ?
L’onde stationnaire possède des points immobiles (qui ne vibrent pas) et d’autres vibrant avec une amplitude
maximale.
 Les repérer sur la simulation.
 Comment nomme-t-on ces points ?
Rappeler la définition de la longueur d’onde.
 Quelle relation lie la longueur d’onde  et la fréquence f de l’onde ?
 Quelle est distance entre 2 nœuds ou 2 ventres consécutifs ?
2. REFLEXION D’UNE ONDE SUR 2 OBSTACLES FIXES :
2.1. Propagation d’une onde non périodique entre 2 points fixes :
L’onde se réfléchit en O et en O’.
Au bout de combien de temps l’onde redevient-elle identique à elle-même ?

TS spécialité 582674228 page 2
2.2. Propagation d’une onde sinusoïdale entre 2 points fixes :
 Dans le cas général, l’onde, de période T, doublement réfléchie est-elle identique à l’onde
incidente ? Quel est alors l’aspect de la corde ?
 A quelle condition l’onde, de période T, doublement réfléchie est-elle identique à l’onde
incidente ?
 En déduire une relation entre la longueur L de la corde et la longueur d’onde .
 A quelle condition obtient-on une onde stationnaire entre les 2 points fixes?
 Quelles fréquences permettent l’obtention d’une onde stationnaire ? Conclure.
3. ETUDE EXPERIMENTALE D'ONDES STATIONNAIRES
Le but de ce paragraphe est de vérifier expérimentalement la relation (1):
vT v
L k k k
2 2 2f
v est la vitesse de propagation de l’onde : elle ne dépend que du milieu de propagation
3.1. Ondes stationnaires le long d’une corde tendue entre 2 points fixes
Dans cette expérience, f est fixée ( c’est la fréquence du vibreur ) et on fait varier L ( longueur de la corde) .
1) Caractéristiques de l’onde stationnaire :
Placer une masse marquée m de 20 g à l'extrémité de la corde.
Faire varier la longueur L de la corde en déplaçant un support afin d'obtenir k=1 fuseau.
 En déduire la valeur de 
 En déduire la valeur de v.
Recommencer avec un nombre de fuseaux k= 2 ….
nombre de fuseaux k
1
2
3
4
longueur de corde L (cm)
 (cm)
v (m/s-1)
Qu’observe-t-on ?Conclure.
Influence des paramètres du dispositif sur le nombre k de fuseaux . :
onde incidente
onde réfléchie en B
onde réfléchie en O
Alimentation
F = 50 Hz
vibreur
corde tendue
masse

TS spécialité 582674228 page 3
F
v
( relation 2)
La tension F est déterminée par la valeur de la masse m accrochée à la corde.
Quels paramètres peut-on faire varier (la fréquence étant fixée à f = 50 Hz)?
a) 1er paramètre : que peut-on déduire du tableau précédent pour  ?
b) 2ème paramètre :
Prendre comme longueur de corde la longueur L trouvée dans le tableau précédent pour m = 20 g et 1 fuseau.
Faire varier la valeur de la masse m et conserver L constante.
 Noter le nombre de fuseaux obtenus.
 Montrer que
km
= cste
L (cm)
m (g)
20
k
1
2
3
4
c) 3ème paramètre :
L’expérience est réalisée au bureau du professeur avec 2 cordes, l’une de masse linéique µ et l’autre de masse
linéique µ’, avec µ’ = 4 µ
La longueur de la corde étant fixée à environ L = 1 m, la masse suspendue étant m = 200g
 Que se passe-t-il si la corde est remplacée par celle de masse linéique µ’, tout en conservant L,
m, f. ?
 Montrer que ce résultat est compatible avec la relation (1)
3.2. Ondes stationnaires dans une colonne d’air :
Le but de ce paragraphe est de vérifier expérimentalement la
relation :
Lk
2
avec :
k
v
f
où
k est le nombre de fuseaux
fk est une fréquence propre du système (= fréquence pour laquelle il
y a une onde stationnaire )
v est la vitesse de propagation de l’onde : elle ne dépend que du
milieu
1) Etude expérimentale dans un tube ouvert:
Placer le micro à l’entrée du tube et rechercher, à l’oscilloscope, la fréquence f4 du quatrième harmonique
 vérifier que
air
4v
f4
2L
En déplaçant le micro dans le tube, déterminer les positions des ventres et des nœuds de pression.
 En déduire le plus précisément possible, la valeur de la longueur d’onde .
Cas d’un tube fermé à l’une de ses extrémités :
Un ventre de vibration se trouve à l’extrémité ouverte et un nœud à l’extrémité fermée.
Pour un mode propre de fréquence fk, quelle est l’expression de la longueur L du tube en fonction de k et  ?
Quelle est la valeur de la fréquence f1 du mode fondamental en fonction de L?