2015-exos06-relativite - leprof

Page 1 sur 3
Exercice 1 : Une ville étrange
Document 1 : Promenade à vélo.
Dans une ville étrange, M. Tompkins fait une promenade à vélo avec un ami. Il passe devant la gare et vérifie
que sa montre indique la même heure que l'hor¬loge : midi. Il poursuit son chemin et arrive alors devant la
poste... « M. Tompkins regarda l'horloge de la poste, qui marquait midi et demi. " Eh bien " remarqua-t-il "cela
nous a tout de même pris une demi-heure. " " Et avez-vous senti passer cette demi-heure ? " demanda son
compagnon. M. Tompkins dut convenir qu'elle lui avait semblé ne durer que quelques minutes. De plus, en
regardant sa montre-bracelet, il vit qu'elle ne marquait que midi cinq. "Oh ! dit-il, l'horloge de la poste avance.
" " Bien sûr, ou bien votre montre retarde, précisément parce que nous allons trop vite." »
D'après G. Gamow, Mr Tompkins in Paperback (1967).
Document 2 : Devant la poste.
Alors M. Tompkins mit sa montre à l'heure de la poste et attendit dix
minutes pour s'assurer qu'elle marchait bien. La montre ne retardait pas.
D'après G. Gamow, Mr Tompkins in Paperback (1967).
Document 3 : Durées entre deux événements.
Le temps propre est le temps mesuré par l'horloge associée au référentiel galiléen dans lequel le système étudié
est au repos (appelé référentiel propre). En particulier, l'intervalle de temps propre entre deux événements est
celui mesuré dans le référentiel galiléen où ces événements ont lieu au même endroit de l'espace.
L'intervalle de temps propre entre deux événements noté t0 , mesuré dans le référentiel propre R, est plus
court que l'intervalle de temps t entre ces mêmes événements mesuré dans un autre référentiel galiléen R' se
déplaçant à la vitesse v par rapport à R :t =
²c²v
1
t0
où c est la célérité de la lumière dans le vide.
Questions
Répondre à l'aide de ses connaissances et des documents.
1- Estimer les durées de la course à vélo :
1.1-t0 mesurée par la montre de M. Tompkins;
1.2-t par l'horloge de la poste.
2- Estimer la durée de l'attente de M. Tompkins devant la poste :
2.1- t0 mesurée par sa montre.
2.2- t par l'horloge de la poste.
3- Dans le texte, quel est le référentiel propre et quelle horloge mesure le temps propre ?
4.1- Estimer la vitesse du vélo de M. Tompkins.
4.2- En fait, le vélo roulait à 25 km.h-1. Une grandeur physique n'a pas sa valeur habituelle dans la ville
étrange imaginée par l'auteur : laquelle et quelle est sa nouvelle valeur ?

Page 2 sur 3
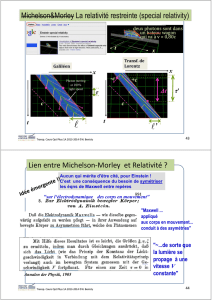
Exercice 2 : L'expérience de Michelson et Morley
Document 1 : Le principe de l'interféromètre.
Albert Michelson avait développé un interféromètre très précis. Le principe consistait à faire interférer deux
faisceaux lumineux, issus d'une même source, après leur avoir fait parcourir des trajets aller-retour égaux, ou
quasiment égaux, dans deux directions perpendiculaires. Les retours étaient obtenus par des miroirs.
D'après www.ac-nice.fr/clea/lunap/html/Relativite/ RelatRestApprof2.htmI
Document 2 : Le dispositif au repos dans R.
Le schéma ci-contre représente les deux parcours suivis par la lumière dans un
référentiel où l'interféromètre est fixe, depuis la lame semi-transparente A :
- jusqu'au miroir B et retour ;
- et jusqu'au miroir C et retour.
Document 3 : Le dispositif en mouvement dans R'.
La Terre sur son orbite se déplace dans le référentiel héliocentrique avec une vitesse
d'environ v = 30 km.s-1 suivant la direction AB. De ce fait, l'interféromètre de Michelson n'est pas fixe dans ce
référentiel, et il se déplace en même temps que se propage la lumière. Le schéma ci-dessous représente les
deux parcours suivis par la lumière dans l'interféromètre de Michelson :
- depuis la lame semi-transparente A jusqu'au miroir C (en C1 à l'instant t1) et retour sur la lame A (en A2 à la
date t2) ;
- depuis la lame semi-transparente A jusqu'au miroir B (en B’1 à l'instant t’1) et retour sur la lame A (en A’2 à
la date t’2 ).
D'après www-obs.univ-lyon.fr/labo/perso/gilles.adam/optionlN
SA/cosmo_4.html
Document 4 : Les résultats.
Michelson et Morley ont utilisé les interférences pour avoir accès au retard de propagation. L'expérience était
montée flottante sur un bain de mercure, de façon à pouvoir l'orienter afin que chaque bras de l'interféromètre
corresponde alternativement au trajet A-B puis au trajet A-C. C'est le déplacement des franges d'interférence
entre ces deux positions qui devait permettre de détecter la variation de la vitesse apparente de la lumière dans
les deux orientations.
Le résultat a été totalement négatif... D'après www-obs.univ-lyonl.fr/labo/perso/gilles.adam/optionl NSA/cosmo_4.html
Questions : Répondre à l'aide de ses connaissances et des documents.
On imagine trois points A, B et C disposés aux trois sommets d'un triangle isocèle rectangle de côté d.
A envoie à t = 0 un signal lumineux vers le miroir B et vers le miroir C. La vitesse de la lumière est c dans R.
1- Supposons les trois points au repos dans le référentiel R.
En exprimant les longueurs des trajets parcourus par la lumière, montrer que les durées de propagation de la
lumière de A en A sont :
1.1- t(ABA)= 2d/c en passant par B ;
1.2- t(ACA)= 2d/c en passant par C.
2- Supposons maintenant que le dispositif se déplace parallèlement à AB à la vitesse v, de A vers B, dans le
référentiel R’.
2.1-Exprimer les durées de propagation de la lumière t(A0B'l) et t(B'1A'2) .
En déduire que t(A0B'1A'2) = ².2d/c . On exprimera .
2.2-Exprimer les durées de propagation de la lumière t(AoC1) et t(C1A2).
En déduire que t(A0C1A2) = 2d/c .
3- Évaluer la valeur de . Pourquoi l'effet attendu était-il extrêmement faible ?
4.1- Définir le référentiel propre adapté à l'expérience.

Page 3 sur 3
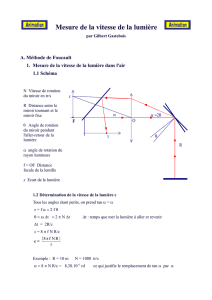
4.2- En quoi la théorie de la relativité explique-t-elle les résultats expérimentaux ?