La poussée d`Archimède

1
La poussée d’Archimède
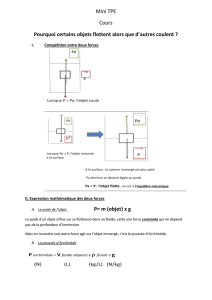
1. Introduction : quelques observations
 Certains objets flottent sur l’eau :
o Un bateau.
o Un morceau de bois.
o Une assiette posée horizontalement.
o Une bouteille en verre vide et fermée.
 Certains objets coulent dans l’eau :
o Un sous-marin en plongée
o Un objet métallique plein
o Une bouteille en verre remplie d’eau
o Une assiette placée verticalement
 Un objet lourd paraît plus léger lorsqu’il est immergé dans l’eau.
On peut déjà en conclure qu’un objet immergé partiellement ou entièrement dans un liquide
subit une force vers le haut qui le fait flotter ou le fait paraître plus léger.
C’est la Poussée d’Archimède (PA)
2. Influence du volume immergé et de la profondeur
a) On suspend un cylindre à un dynamomètre.
On mesure son poids.
On trempe l'objet dans l'eau, à différentes profondeurs.
Le dynamomètre nous donne le "poids apparent" de l'objet trempé dans l'eau.
La différence entre le poids du cylindre et l’indication du dynamomètre est égale à la
poussée d’Archimède.
1,30 N
1,10 N
1,00 N
0,85 N
0,85 N
PA= 0 N
PA= 0,20 N
PA= 0,30 N
PA= 0,45 N
PA= 0,45 N

2
b) Constatations
 Le cylindre pèse 1,3 N.
 L’indication du dynamomètre diminue progressivement quand on enfonce le cylindre
dans l’eau.
 Le dynamomètre indique 0,85 N quand le cylindre est complètement immergé.
 L’indication ne change plus lorsque le cylindre s’enfonce davantage.
c) Conclusions
 La poussée d’Archimède sur un objet dépend du volume immergé, elle augmente quand
le volume immergé augmente.
 La poussée d’Archimède sur un objet complètement immergé ne dépend pas de sa
profondeur.
d) Explications
Le liquide dans lequel l’objet est immergé exerce une force pressante sur toute sa surface.
Les schémas ci-dessous représentent les forces pressantes s’exerçant sur un
parallélépipède immergé.
Les forces s’exerçant sur les parois latérales se compensent.
 L’objet est partiellement immergé :
La poussée d’Archimède est due à la force pressante exercée, vers le haut sur la surface
inférieure de l’objet.
Cette force augmente quand l’objet s’enfonce dans le liquide.
 L’objet est totalement immergé :
La surface inférieure de l’objet subit une force vers le haut.
La surface supérieure subit une force vers le bas.
La surface inférieure étant à une profondeur plus grande, elle subit une force vers le haut
plus importante que la force exercée vers le bas sur la surface supérieure.
La poussée d’Archimède est la résultante des forces pressantes exercées par l’eau sur
l’objet, elle est dirigée vers le haut.

3
3. Influence de la forme et de la position
a) On mesure le poids apparent d'un bloc de plasticine complètement immergé dans l'eau.
On donne au bloc différentes positions et différentes formes.
b) Constatation: l’indication du dynamomètre est toujours la même.
c) Conclusion
 La poussée d’Archimède sur un objet trempé dans un liquide ne dépend ni de sa forme
ni de son orientation.
 Elle ne dépend que du volume immergé.
4. Influence du liquide
a) Dans l’eau (eau= 1000 kg/m³)
la poussée d’Archimède vaut 0,45 N.
Dans l’huile (huile= 880 kg/m³)
la poussée d’Archimède vaut 0,40 N.
b) Conclusion : la poussée d’Archimède
dépend de la masse volumique du
liquide.
Elle augmente avec celle-ci.
0,7N
0,7N
0,7N
0,7 N
1,30 N
0,85 N
0,90 N
eau
huile
u

4
5. Calcul de la poussée d’Archimède
Comme la poussée ne dépend pas de la forme de l’objet, calculons-la dans le cas le plus
simple : un parallélépipède de hauteur H et de surface horizontale S.
Le volume du parallélépipède vaut : V = S H
La surface supérieure se trouve à une profondeur h1.
La surface inférieure se trouve à une profondeur h2.
H = h2 - h1
Force 1 exercée vers le bas, sur la face supérieure :
F1 = p1S = liq g h1 S
Force 2 exercée vers le haut, sur la face inférieure :
F2 = p2S = liq g h2 S
La poussée d’Archimède est la force résultante.
Elle est dirigée vers le haut et est égale à la différence entre F2 et F1 .
PA = F2 - F1 = liq g h2 S - liq g h1 S = liq g (h2 – h1 ) S = liq g H S = liq g Vim
Donc PA = liq g Vim
PA: poussée d'Archimède (N)
liq: masse volumique du liquide (kg/m³)
g: coefficient de pesanteur (N/kg)
Vim: volume immergé (m³)
La poussée d’Archimède est donc égale au poids d’un volume de liquide égal au volume
immergé de l’objet.
6. Enoncé du principe d’Archimède
Un objet plongé dans un liquide (entièrement ou partiellement) subit de la part de
celui-ci une force verticale vers le haut égale au poids du liquide déplacé
(poids d’un volume de liquide égal au volume immergé de l’objet)
7. Conséquences
 Si la poussée d’Archimède est inférieure au poids de l’objet,
l’objet s’enfonce dans le liquide.
 Si la poussée d’Archimède est supérieure au poids de l’objet,
l’objet remonte vers la surface.
A
L’objet coule
A
L’objet flotte
h2
1
2
h1
h2
1
2
H

5
 Si la poussée d’Archimède est égale au poids de l’objet, l’objet est en équilibre (il reste
immobile). C’est le cas d’un objet qui flotte à la surface du liquide.
 Condition pour qu’un objet plein et homogène flotte.
Il faut que, lorsqu’il est complètement immergé, que la poussée d’Archimède (PA ) soit
supérieure à son poids (G).
Donc, un objet (de volume V) flotte si PA > G ou liq g V > obj g V
ou liq > obj
De même, un objet coule si liq < obj
Un objet plein et homogène flotte à la surface d’un liquide si sa masse volumique est
inférieure à celle du liquide. Il coule si elle est supérieure.
8. Les objets flottants
a) Quand un objet flotte, immobile, à la surface d’un liquide, la
poussée d’Archimède (A) exercée par le liquide sur l’objet (vers
le haut) est égale à son poids ( ) (dirigé vers le bas).
liq g Vim = G
Le poids du volume de liquide déplacé est égal au poids de
l'objet.
Un objet flottant immobile déplace son propre poids de liquide.
b) Le bateau
Comment se fait-il qu'un bateau, qui est construit en métal, un
matériau plus lourd que l'eau, puisse flotter ?
Un bateau n'est pas composé que de métal. Il contient de l’air, il
est creux.
c) Le ludion
 C'est un petit objet creux ouvert à sa partie inférieure. Il est partiellement rempli d'eau de
telle manière qu'il flotte "tout juste" à la surface de l'eau. (Une légère surcharge le ferait
couler).
 Le récipient qui contient l'eau est fermé et peut-être comprimé.
 Quand on le comprime, le ludion coule.
A
liq < obj : l'objet coule
liq > obj : l'objet flotte
liq = obj : l'objet est en équilibre dans le liquide