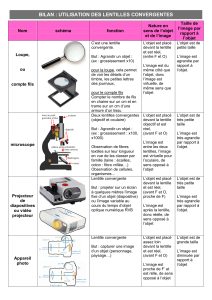
PG17. Lentille épaisse concave –convexe

1
Exercices d’Optique géométrique
PG1. Dioptre sphérique convexe
Soit un bâton en verre d’indice n2 =1,5, la face au soleil a un rayon de courbure r= 50 cm
A)-A quelle distance du sommet du dioptre doit se situer l’objet si nous désirons que
l’image soit placée à + 7cm ?
B)- A quelle distance du sommet du dioptre doit se situer l’objet si nous désirons que
l’image soit placée à - 7cm ?
C) Soit un bâton dont la face au soleil a un rayon de courbure de +25cm, n1 = 1, n2 = 1.33
- Tracer le graphe des valeurs de xi en fonction des variations de xo
- Solution graphique, tracer la position de l’image et ses caractéristiques pour les
deux exemples suivants :
– objet réel placé avant le foyer objet
– objet réel placé après le foyer objet
– objet virtuel placé avant le foyer image
- objet virtuel placé après le foyer image
________
PG2. Bâton en plastique placé dans l’eau, calcul de la position de l’image
Un bâton en plastique, d’indice n1 = 1.5, de longueur 70 cm, est plongé verticalement et
partiellement dans l’eau. Un objet est placé sur la face plane du bâton sortant dans l’air et
reçoit les rayons du soleil, l’autre extrémité placée dans l’eau est concave de rayon r=-4cm,
l’indice de l’eau est n3=1,33
Calculer la position de l’image et ses caractéristiques.
_______
PG3. Dioptre sphérique concave
Un bâton de verre, indice, n2 = 1,5 a une extrémité une face sphérique de rayon r=-50cm
A-A quelle distance de la face d’entrée doit se trouver un objet placé dans l’air afin que
son image soit située à une distance de +5cm du sommet ?
B- A quelle distance de la face d’entrée doit se trouver un objet placé dans l’air afin que
air, n1 = 1
eau, n3 = 1.33
n2 =1.5

2
son image soit située à une distance de -5cm du sommet ?
C- Un autre bâton a sa face d’entrée ayant un rayon r=25cm son indice est n2 = 1.33
avec n1 = 1.
- Tracer le graphe des valeurs de xi en fonction des variations de xo
- Solution graphique, tracer la position de l’image et ses caractéristiques pour les
deux exemples suivants :
– objet réel placé avant le foyer image
– objet réel placé après le foyer image
– objet virtuel placé avant le foyer objet
- objet virtuel placé après le foyer objet
________
PG4. Film plastique sur la surface de l’eau, l’interface est considérée comme ayant la
forme d’un dioptre sphérique
Un film plastique est monté sur un anneau et l’ensemble est placé sur la surface de l’eau.
Le film forme un dioptre sphérique rempli d’eau, nous négligeons l’épaisseur du film,
nous obtenons donc une surface concave sphérique contenant de l’eau d’indice n2 = 1.33.
Les rayons du soleil sont normaux sur l’interface et l’image du soleil est observée à une
profondeur de 100cm.
Calculer le rayon de courbure de ce dioptre sphérique d’eau.
Air n1 = 1
Eau n2=1.33 ________
PG5. Lentille d’air contenu dans un matériau plastique.
Un bâton plastique, indice n2=1.5, de section circulaire a une extrémité plane,
l’autre est une surface sphérique concave par rapport au faisceau de lumière
incidente issue du soleil et dirigé perpendiculairement à la face plane d’entrée,
le rayon de courbure est r= -10 cm. Un deuxième bâton identique au premier
est placé dans le prolongement du premier mais sa face sphérique est contre la
face de sortie du premier bâton. Il y a donc formation d’une lentille mince
d’air entre les deux bâtons, indice de l’air n1=1.
Un objet est placé sur la face d’entrée du premier bâton il se trouve à une
distance de 20cm de la lentille mince.
Calculer la position de l’image formée par ce système.
_______

3
PG6. Lentille mince placée sur l’eau
Une lentille mince biconvexe r=-r'=10 cm, ayant dans l’air une distance focale f=10cm est
placée sur la surface de l’eau, la face d’entrée est donc au contact de l’air, la face de sortie
au contact de l’eau
indice de l’air : n1 = 1
indice du verre: n2 = 1.5
indice de l’eau : n3 = 1.33
A)-La lentille est éclairée par le soleil. Calculer la distance de l’image du soleil située
dans l’eau.
B)- quelle est cette distance si la lentille était faite en silice d'indice n= 3.4
___________
PG7. Loupe
Une loupe de distance focale f1 = 12cm est placée à 8 cm devant l’œil
Calculer xo1 abscisse de l’objet, le grandissement et le grossissement
-quand l’image est au punctum proximum
- quand l’image est à l’infini _______
PG8. Microscope (montage de 3 lentilles)
Distance focale de l’objectif : fob = .31cm
Distance focale de l’oculaire : foc = 1.79cm
Distance focale de l’œil de l’observateur : foe = 2cm
L’image intermédiaire formée par l’objectif est située à 16cm de l’objectif
La distance objectif-oculaire est de 18cm
L’œil regarde dans la configuration du minimum de vision distincte qui rappelons le est de
–25cm
Calculer : -grandissement de l’objectif
- grandissement de l’oculaire
- grandissement total de ces 2 objectifs et le comparer avec le grossissement
angulaire que l’étudiant calculera.
- ________
air n1 = 1
eau n3 = 1.33
n2 = 1.5

4
PG9. Microscope-observation au minimum de vision distincte
Distance focale de l’objectif : fob = .31cm
Distance focale de l’oculaire : foc = 1.31cm
Distance focale de l’œil de l’observateur : foe = 2cm
L’image intermédiaire formée par l’objectif est située à 16cm de l’objectif
L’œil regarde l’image qui est située au punctum proximum
A- A quelle distance de l’objectif, l’objet est-il placé ?
B-Calculer la distance de l’image intermédiaire formée par l’objectif par rapport à
l’oculaire
C- Calculer la distance objectif-oculaire, c’est à dire la longueur totale du microscope.
A- Calculer le grossissement. _______
PG10- . Microscope-observation à -l’infini
Distance focale de l’objectif : fob = 2.15cm
Distance focale de l’oculaire : foc = 1.3cm
Distance focale de l’œil de l’observateur : foe = 2cm
L’image intermédiaire formée par l’objectif est située à 16cm de l’objectif
L’œil regarde l’image formée par l’oculaire, image située à – l’infini
A- A quelle distance de l’objectif, l’objet est-il placé ?
B-Calculer la distance de l’image intermédiaire formée par l’objectif par rapport à
l’oculaire
C- Calculer la distance objectif-oculaire, c’est à dire la longueur totale du microscope.
B- Calculer le grossissement _______
G11. Lunette astronomique de Képler
Proposer une conception de la lunette astronomique de Képler ayant un grossissement de
4 ou de 10
A partir de quelle valeur de grossissement la construction de ce télescope devient
irréalisable ? Pourquoi ? ______
PG12. Lunette astronomique de Galilée
La distance de l’objectif est f1= 30cm
La distance focale de la deuxième lentille est négative: f2 =9.9cm.
La distance entre ces deux lentilles est xo1= 20cm = f1+ f2
A- A quelle distance de l’objectif, l’objet est-il placé ?
B-Calculer la distance de l’image intermédiaire formée par l’objectif par rapport à
l’oculaire
C- Calculer la distance objectif-oculaire, c’est à dire la longueur totale du microscope.

5
D- Calculer xi2 l’abscisse de l’image finale par rapport à la deuxième lentille
C- Calculer le grossissement, montrer que pour un objet placé à –l’infini, nous avons à
nouveau : G= -f1/f2 _______
PG13. Extension d’un faisceau laser
Le diamètre d’un faisceau laser est de 2mm, nous désirons le transformer un diamètre de
20mm
A-Montage formé d’une lentille biconvexe et d’une lentille biconcave
Le faisceau traverse d’abord la lentille biconvexe de distance focale –mm.
La lentille biconcave a une distance focale de 30mm, son diamètre est de 30mm
Déterminer par une construction géométrique l’emplacement de cette deuxième
lentille ?
B- Montage formé par deux lentilles biconvexes.
La première lentille a une distance focale f1=5mm
La deuxième lentille a une distance focale f2= 50mm
Déterminer par une construction géométrique l’emplacement de cette deuxième
lentille?
En déduire le diamètre approximatif de ces lentilles
_______
PG14. Exercice de multiplication de matrices
Soient deux systèmes de coordonnées rectangulaires cartésiens, x, y et x’, y’, le deuxième
est obtenu à partir du premier par une rotation de d’un angle 
A-Etablir la matrice de rotation x, y  x’, y’
 cos  sin   1,1 1,2
A =   =
 -sin  cos   2,1 2,2
Cette matrice représente une rotation de x, y vers x’y dans le sens positif de rotation
des mathématiciens.
B-La matrice de rotation dans le sens opposé désignée par A-1 s’obtient en remplaçant 
par - 
- Ecrire cette nouvelle matrice
- Montrer que la matrice B=AA-1 est la matrice unité
C- La matrice transposée de A est désignée par AT, nous l’obtenons par permutation de
2,1 et 1,2 de A.
Constater que dans cet exemple AT = A-1, le produit AAT est aussi une matrice unité.
D- Montrer que la matrice résultante du produit A()A() est la matrice
A(2), c’est à dire A(2) = A() A()
_______