2006-2007 Sadiki

1
Collège Sadiki
Devoir de contrôle n° : 3
Sciences physiques
3 M1
Vendredi 22 -4-2006
Prof : Cherchari
 On donnera l’expression littérale avant de passer à l’application numérique.
 L’utilisation de la calculatrice non programmable est autorisée.
 Numéroter les questions.
Durée : 2 heures
Exercice : 1 ( 3 pts)
Pour chacune des équations suivantes :
MnO4- + Fe2+ Mn2+ + Fe3+
ClO- + H2S Cl- + S
S2O82- + I- SO42- + I2
H2O2 + Cr2O72- O2 + Cr3+
1/ Donner en le justifiant les deux couples redox mis en jeu dans chaque équation chimique.
2/ Etablir les demi-équations rédox en précisant l’oxydation et la réduction.
3/ Déduire l’équation bilan pour chaque cas.
Exercice n : 2 ( 4 pts )
On prépare d'une solution S de sulfate de cuivre II de concentration C=0.5 mol.L-1 en dissolvant
une masse m de cette substance dans 100cm3 d’eau distillée. La dissolution s’effectue sans variation
de volume de la solution.
1/ Ecrire l’équation d’ionisation du sulfate de cuivre II dans l’eau et calculer la masse m. On donne
MCu= 63,5 g.mol-1 ; MS=32 g.mol-1 et MO= 16 g.mol-1 .
2/ On introduit dans un bécher une quantité de zinc de masse m1 = 6,5 g et un volume V de la solution
S. A la fin de la réaction on remarque l’apparition d’un dépôt rouge brique de masse m2 = 3,17 g.
a- Décrire la réaction qui se produit.
b- Ecrire l’équation de la réaction. Donner les couples rédox mis en jeu.
c- Montrer que le zinc est le réactif utilisé en excès. Calculer le volume V.
d- Calculer la masse de zinc restante.
e- Calculer la concentration de la solution en ions Zn2+.
On donne MZn=65.4 g.mol-1.
f- Quel volume minimal d’une solution de nitrate
d’argent de concentration molaire C’ = 0,4 mol.L-1
faut-il ajouter au bécher pour faire réagir toute la
quantité de zinc et de cuivre.
Exercice 1 (6,5 pts) :
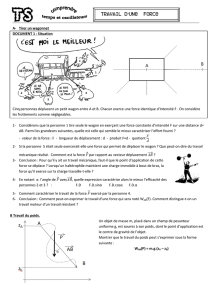
Un avion de guerre
supersonique est animé d’un mouvement rectiligne
uniforme à la vitesse V0 = 400 m.s-1 vole à une
altitude de 2000 m, son radar a détecté un
véhicule de transport de soldats ennemis supposé
ponctuel, immobile au point A, le pilote a décidé de
les attaquer, malgré l’interdiction de ce fait par la loi
de Genève. En passant par O origine du repère
(O,i,j) l’avion a lâché, à une date prise comme origine de temps, une bombe qui après quelques
secondes a détérioré complètement le véhicule et a tué tous les soldats.
Physique ( 13 points )
Chimie ( 7 points )
O
i
j
V0
x
y
2000 m

2
1- En négligeant la force résistance de l’air et en appliquant la relation fondamentale de la dynamique à
la bombe déterminer les composantes selon l’axe (0,x) et selon l’axe (O,y) de son accélération.
2- Etablir les lois horaires de mouvement de la bombe selon les deux axes.
3- Endéduire l’équation de la trajectoire de la bombe relativement au repère (O,i,j).
4- A quelle distance de la verticale passant par O se trouvait le véhicule ? Déterminer la date d’arrivée
de la bombe au véhicule.
5- Où se trouvait l’avion à la date d’arrivée de la bombe au véhicule ?
6- Déterminer les caractéristiques du vecteur vitesse de la bombe lorsqu’elle se trouvait à 1000 m au
dessus du sol.
Exercice 2 (6,5 pts) :
Un train est formé par une locomotive de masse m2 et un wagon de masse m1 = 104 Kg
(m2 = 2m1). Le wagon est attaché à la locomotive à l’aide d’un ressort à spires non jointives de masse
négligeable et de constante de raideur K = 105 N.m-1 .La locomotive et le wagon chacun est soumis à
une force de frottement f supposée constante de valeur égale à 15.103 N. La locomotive développe une
force motrice supposée constante F qui sert à mettre le train en mouvement. A l’origine des dates le
train prend départ du point A sans vitesse initiale et parcourt le trajet horizontal AB = 200 m en 10 s
et arrive en B à la vitesse VB.
1- a- Etablir l’expression de l’accélération a de mouvement du train. Endéduire la nature de son
mouvement.
b- Calculer a. Endéduire la valeur de VB.
c- Calculer la valeur de la force motrice F.
d- Déterminer l’allongement du ressort.
2- Au point B le train aborde avec la vitesse constante VB un plan incliné dont la ligne de plus
grande pente fait un angle  = 30° avec l’horizontale et la locomotive développe au cours de
cette montée une force motrice F’.
a- Calculer la valeur de la force motrice F’.
b- Calculer l’allongement du ressort.
c- Au point C le ressort est cassé, Montrer que le mouvement ultérieur du wagon comporte deux
phases.
d- Déterminer la distance parcourue par le wagon avant de rebrousser chemin.
A
B
C