Essai de systèmes N°6

Essai de systèmes N°6
Etude de la sonde de Hall et de quelques utilisations
Buts de l’essai : On veut étudier un capteur extrêmement répandu qui permet de mesurer, avec une
isolation galvanique, les courants et les tensions. On commencera par donner les bases
régissant le principe de ce capteur. On étudiera ensuite une utilisation importante, à savoir
le transformateur à effet Hall, et une utilisation plus ludique : le détecteur de métaux.
I Principe de fonctionnement du capteur de Hall
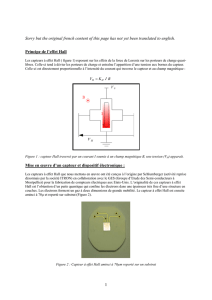
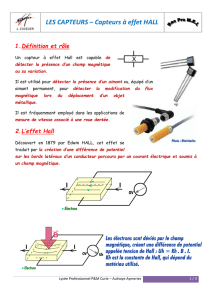
Une puce de silicium est traversée par un courant selon l’axe des x et est en même temps soumise à un
champ magnétique selon l’axe des y (voir figure 1).
Les électrons de la puce de silicium, de charge –e, sont soumis à la force de Lorentz (voir ou revoir le
cours sur les particules chargées en mouvement dans un champ magnétique
B
).
Cette force s’écrit
BveF  .
1
et elle est dirigée selon l’axe des z.
Il en résulte que les électrons sont déviés vers le bas et sont en surnombre sur la face du bas.
Il se crée alors un champ électrique
E
(comme pour un condensateur) qui donne naissance, entre les
faces, à une différence de potentiel
dEVH.
(où d est la distance entre les faces).
A l’équilibre, ce champ agit sur les électrons en imposant une force
EeF .
2
telle que
0
21  FF
.
Figure 1
L’effet Hall est la création de ce champ électrique
E
pour compenser l’effet du champ magnétique
B
.
De plus, VH est proportionnelle à B et à I : on pourra donc, en mesurant VH, avoir une mesure de B ou de I.
 Indiquer, sur un schéma, le sens de I, le sens de
B
, le sens de
E
, les directions et les sens des forces
1
F
et
2
F
.
 Si on fait passer un courant constant connu I, quelle sera l’allure de la courbe VH = f(B) ?
Essai N°6 BTS ELECTROTECHNIQUE Page 1/6
I I
z
x
y
V
S
B
H
-- - - -- -
-
-
+++ +++ + ++ +
+
I
V
B
H

II Principe du transformateur à effet Hall
A partir de la tension VH de sortie du capteur de Hall, on va créer un courant I2 qui va passer dans les N2
spires du bobinage secondaire enroulé autour du même noyau de fer que celui où sont enroulées les N1 spires
du bobinage primaire parcouru par le courant I1 (voir figure 2).
Figure 2
On va alors, par un dispositif électronique simple, faire en sorte que le champ magnétique total à
l’intérieur de l’entrefer soit nul (boucle de rétroaction).
A ce moment, le courant I2 sera l’image de I1 et on pourra, à l’aide de I2, mesurer I1.
II.1 Etude d’un circuit magnétique
a) Rappeler ce que signifie le point au-dessus du bobinage parcouru
par le courant I1.
b) Ecrire l’équation aux ampère-tours liant N1, I1, le flux Φ à travers
le circuit fer et la réluctance R du circuit magnétique.
II.2 Etude du transformateur d’intensité Figure 3
II.2.1 Ecrire l’équation aux ampère-tours liant
N1, N2, I1, I2, le flux Φ à travers le circuit fer
et la réluctance R du circuit magnétique
de la figure 4.
II.2.2 Le secondaire du transformateur est fermé
sur une résistance R grande devant la résistance
interne du transformateur. L’inductance de fuite totale
ramenée au secondaire vaut L2, comme indiqué sur la
figure 5.
Figure 4
L2
Figure 5
II.2.2.1 Ecrire l’équation électrique reliant N2, le flux Φ et U2.
Essai N°6 BTS ELECTROTECHNIQUE Page 2/6
R
I1
I2
V
v
I's
N2
Vcc+
Vcc-
(b)
(a)
H
N1
I1
R
I1 I2
U2
I1
I2

II.2.2.2 Ecrire l’équation électrique reliant N2,
2
I
, R, L2 et .
II.2.2.3 On rappelle qu’en régime sinusoïdal, on peut remplacer les
dérivées par des multiplications par « j.ω ». Déduire alors des deux
paragraphes précédents qu’en régime sinusoïdal, le flux complexe
vaut :
2
2
2.
.. .. I Nj LjR
II.2.3 En se servant de II.2.1 et de II.2.2, exprimer, en régime sinusoïdal, le rapport
1
2
I
I
en fonction de N1,N2, R, L2, R et ω.
II.2.4 Vers quoi ce rapport tend-il lorsque ω → 0 ?
II.2.5 Conclure sur l’utilité du transformateur d’intensité (TI) en continu.
II.3 Etude du transformateur à effet Hall (figures 2 et 6)
II.3.1 Ecrire l’équation aux ampère-tours liant N1, N2, I1, I2, Φ et
R . Quel est le
changement principal par rapport à la question II.2.1 ?
II.3.2 Montrer qu’on peut écrire : N1.I1 – N2.I2 = K.B
Exprimer K en fonction de R et de S (section du circuit magnétique). On gardera
cette notation par la suite.
Figure 6
II.3.3 La tension VH à la sortie de la sonde de Hall s’écrit : VH = VH0 + a.B
Exprimer V’H en fonction de R1, R2, a, B, VP et VH0. A quelle condition a-t-on
V’H = a’.B ? Donner l’expression de a’ en fonction des données du problème.
II.3.4 Exprimer v en fonction de V’H, R’1 et R’2. Montrer alors que la tension v est
proportionnelle au champ magnétique : v = K’.B .
Exprimer K’ en fonction de a, R1, R2, R’1 et R’2.
II.3.5 Montrer que
22 ... ILjRV
lorsque le courant I2 est sinusoïdal, de
pulsation ω.
Essai N°6 BTS ELECTROTECHNIQUE Page 3/6
-
+S- +S
R1
R1 R2
R'1
R'2
L2
R
V
VV' v
I2
+Vcc
-Vcc
T1
T2
D2
D1
A1 A2
H
H
P

II.3.6 A partir des trois équations des paragraphes II.3.5, II.3.4 et II.3.2, exprimer le
rapport
1
2
I
I
en courant continu, en fonction de N1, N2, K et K’.
II.3.7 On suppose que N2 est très grand devant
'
.
KRK
, ce qui arrive souvent (voir
l’exemple de l’annexe où N1 = 1, alors que N2 = 2000).
Que devient alors le rapport
1
2
I
I
?
Conclure : comment utiliser ce montage pour mesurer I1 ?
Pourquoi lui donne-t-on le nom de transformateur à effet Hall ?
II.3.8 Lire la documentation constructeur sur un capteur de courant à effet Hall.
Encadrer la dizaine de lignes qui rappelle le principe du fonctionnement de ce
capteur, et donner quelques utilisations que propose le constructeur.
III Utilisation comme détecteur de métaux ferromagnétiques
On considère un solénoïde comportant N spires.
III.1 En vous aidant de la figure
ci-dessous où on a déposé
de la limaille de fer dans le
solénoïde, dessiner les lignes
de champ et, en quelques points,
le champ magnétique.
III.2 On place une sonde de Hall à l’intérieur du solénoïde. On mesure un champ B0 lorsque le
solénoïde est parcouru par un courant I0.
A la sortie de l’appareil qui mesure B0 (teslamètre), on a la possibilité de recueillir une
tension continue V0 proportionnelle à B0. Cette tension est trop faible pour allumer une
LED (la tension de seuil d’une LED rouge est d’environ 1,5 V). Donner le montage à
amplificateur opérationnel nécessaire pour amplifier V0 = 30 mV et obtenir une tension
V’0 = 1,5 V. On précisera les valeurs des résistances nécessaires à ce montage. La LED
va-t-elle s’allumer ?
III.3 On place dans le solénoïde un outil ferromagnétique. Comment cet outil va-t-il modifier
les lignes de champ dans le solénoïde ?
En déduire l’état de la diode lorsqu’on place l’outil.
Essai N°6 BTS ELECTROTECHNIQUE Page 4/6
R
LEDVo V'o
AMPLI

IV Manipulations
IV.1 Etude du capteur de Hall
Celui-ci est constitué de la maquette appelée « sonde de Hall » et correspond, sur la figure 6, à la partie
située entre VH et V’H. Prendre une bobine de N1 = 250 spires que l’on placera sur le noyau de fer.
Placer la sonde dans l’entrefer et mesurer V’H lorsque I1 = 0. Agir sur le potentiomètre de 10 k de la
maquette pour faire le zéro (on doit avoir V’H = 0 si I1 = 0).
Alimenter la bobine en limitant le courant à 1 A. Régler l’amplification de la maquette (potentiomètre
de 470 k) pour avoir V’H = 5 V pour I1 = 1 A.
Tracer la courbe V’H = f(I1), pour I1 croissant de 0 à 1,5 A.
Quelle est l’allure de cette courbe ? Relever les paramètres intéressants.
Tracer ensuite la courbe V’H = f(I1), pour I1 décroissant de 1,5 A à 0.
Voit-on le phénomène d’hystérésis ?
IV.2 Utilisation comme détecteur de métaux ferromagnétiques
On prendra le solénoïde dans sa totalité et le capteur de Hall sera placé au centre du solénoïde.
Faire le zéro du teslamètre pour le plus petit calibre en l’absence de champ magnétique.
Placer en sortie du teslamètre le montage amplificateur déterminé au paragraphe III.2, la LED et
R = 68 .
A l’aide d’une alimentation stabilisée, imposer un courant I1 = 1,5 A dans le solénoïde, et relever les
valeurs de B0 et V0.
La LED s’allume-t-elle ?
Placer une feuille de papier à l’intérieur du solénoïde : que se passe-t-il ?
Agir de même avec un outil ferromagnétique (tournevis ou clé à pipe) en faisant attention de ne pas
heurter la sonde de Hall très fragile : que se passe-t-il ? Expliquer les différentes phases de l’expérience.
IV.3 Comparaison entre un transformateur d’intensité et un transformateur à effet Hall
On veut visualiser la
différence entre un transformateur
d’intensité (TI) et un transformateur
à effet Hall.
D’après la préparation,
quelle doit être la différence quand
on mesure un courant continu ?
On propose un montage
permettant de générer un courant
presque continu.
Rappeler pourquoi ce montage permet d’obtenir un courant continu : on tracera la forme de la tension
en sortie du pont et on précisera quel est le composant qui permet d’obtenir I continu.
R est un rhéostat [100  ; 1,8 A] avec curseur environ au milieu. Placer le primaire du TI (gros fils)
dans le circuit, ainsi qu’un ampèremètre. Régler le rhéostat pour avoir environ
I
= 1,0 A.
Attention : le secondaire d’un TI (fils fins) doit TOUJOURS être en court-circuit : on placera
entre les bornes du secondaire un ampèremètre dont on aura pris soin de vérifier qu’il n’est pas grillé.
Visualiser sur CH1 le courant I par une sonde de courant (AM30 : elle fonctionne sous le principe de
l’effet Hall), et visualiser sur CH2 la tension aux bornes de l’ampèremètre du secondaire du TI (elle est l’image
du courant dans le secondaire).
Noter les différences et les similitudes des deux courbes, puis conclure sur l’utilité des deux
transformateurs pour mesurer des courants continus. On pourra faire deux relevés : l’un pour la plus petite
valeur de L possible, l’autre pour la plus grande valeur possible de L.
Essai N°6 BTS ELECTROTECHNIQUE Page 5/6
R
L
48 V
I
CH2
PONT DE DIODES
MONOPHASE
TI
50 Hz
MX 53 ou MX 54
utilisé en calibre mA
(il indique l'état de son fusible)