FONCTION LOGARITHME NEPERIEN En 1614, un mathématicien

Yvan Monka – Académie de Strasbourg – www.maths-et-tiques.fr
FONCTION LOGARITHME
NEPERIEN
En 1614, un mathématicien écossais, John Napier (1550 ; 1617) ci-
contre, plus connu sous le nom francisé de Neper publie « Mirifici
logarithmorum canonis descriptio ».
Dans cet ouvrage, qui est la finalité d’un travail de 20 ans,
Neper présente un outil permettant de simplifier les calculs
opératoires : le logarithme.
Toutefois cet outil ne trouvera son essor qu’après la mort de Neper.
Les mathématiciens anglais Henri Briggs (1561 ; 1630) et William
Oughtred (1574 ; 1660) reprennent et prolongent les travaux
de Neper.
Les mathématiciens de l’époque établissent alors des tables de logarithmes de plus en plus
précises.
L’intérêt d’établir ces tables logarithmiques est de permettre de substituer une multiplication
par une addition (paragraphe II). Ceci peut paraître dérisoire aujourd’hui, mais il faut
comprendre qu’à cette époque, les calculatrices n’existent évidemment pas, les nombres
décimaux ne sont pas d’usage courant et les opérations posées telles que nous les utilisons ne
sont pas encore connues. Et pourtant l'astronomie, la navigation ou le commerce demandent
d’effectuer des opérations de plus en plus complexes.
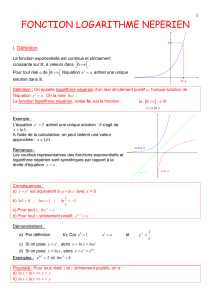
I. Définition
La fonction exponentielle est continue et
strictement croissante sur , à valeurs dans
0;
.
Pour tout réel a de
0;
l'équation
exa
admet une unique solution dans .
Définition : On appelle logarithme népérien d'un réel strictement positif a, l'unique
solution de l'équation
exa
. On la note
lna
.
La fonction logarithme népérien, notée ln, est la fonction :
ln : 0;
°
xalnx
Exemple :
L'équation
ex5
admet une unique solution. Il s'agit de
xln5
.
A l'aide de la calculatrice, on peut obtenir une valeur approchée :
x1,61
.

Yvan Monka – Académie de Strasbourg – www.maths-et-tiques.fr
Remarque :
Les courbes représentatives des fonctions exponentielle et logarithme népérien sont
symétriques par rapport à la droite d'équation
yx
.
Conséquences :
a)
ylnx avec x 0xey
b)
ln10
;
lne1
;
ln1
e 1
c) Pour tout x,
lnexx
d) Pour tout x positif,
eln xx
Démonstrations :
a) Par définition
b) - Car
e01
- Car
e1e
- Car
e11
e
c) Si on pose
yex
, alors
xln ylnex
d) Si on pose
ylnx
, alors
xeyeln x
Exemples :
eln2 2
et
lne44
Propriété : Pour tous réels x et y strictement positifs, on a :
a)
lnxln yxy
b)
lnxln yxy
Démonstration :
a)
xyeln xeln ylnxln y
b)
xyeln xeln ylnxln y

Yvan Monka – Académie de Strasbourg – www.maths-et-tiques.fr
Méthode : Résoudre une équation ou une inéquation
Résoudre dans les équations et inéquations suivantes :
a)
lnx2
b)
ex15
c)
3lnx48
d)
ln 6x1
 2
e)
ex54ex
a)
lnx2
lnxlne2
xe2
La solution est
e2
.
b)
ex15
ex1eln5
x1ln5
xln51
La solution est
ln51
.
c)
3lnx48
3lnx12
lnx4
lnxlne4
xe4
La solution est
e4
.
d)
ln 6x1
 2
ln 6x1
 lne2
6x1e2
xe21
6
L'ensemble solution est donc
e21
6;
.
e)
ex54ex
ex4ex 5
 3ex 5
ex5
3
exeln 5
3
xln 5
3
L'ensemble solution est donc
;ln 5
3
.

Yvan Monka – Académie de Strasbourg – www.maths-et-tiques.fr
II. Propriété de la fonction logarithme népérien
1) Relation fonctionnelle
Théorème : Pour tous réels x et y strictement positifs, on a :
ln xy
 lnxln y
Remarque : Cette formule permet de transformer un produit en somme.
Démonstration :
eln(xy)xyeln xeln yeln xln y
Donc
ln xy
 lnxln y
Corollaires : Pour tous réels x et y strictement positifs, on a :
a)
ln 1
x lnx
b)
ln x
ylnxln y
c)
ln x1
2lnx
d)
ln xn
 nlnx
avec n entier relatif
Démonstrations :
a)
ln 1
xlnxln 1 xx
ln10
b)
ln x
yln x1 y
lnxln 1
ylnxln y
c)
2ln xln xln xln xx
 lnx
d)
enln xeln x
nxneln xn
Donc
nlnxln xn
Exemples :
a)
ln 1
2
 ln2
b)
ln 3
4
ln3ln4
c)
ln 5 1
2ln5
d)
ln64 ln 82
 2ln8
Méthode : Simplifier une expression
Aln 35
 ln 35
B3ln2 ln52ln3
Clne2ln 2
e

Yvan Monka – Académie de Strasbourg – www.maths-et-tiques.fr
Aln 35
 ln 35
ln 35
 35
ln 9 5
ln4
B3ln2 ln52ln3
ln23ln5ln32
ln 235
32
ln 40
9
Clne2ln 2
e
2lneln2 lne
2ln2 1
3ln2
Méthode : Résoudre une équation
1) Résoudre dans l'équation :
6x2
2) Résoudre dans
0;
l'équation :
x53
3) 6 augmentations successives de t % correspondent à une augmentation globale
de 30 %. Donner une valeur approchée de t.
1)
6x2
ln 6x
 ln2
xln6 ln2
xln6
ln2
La solution est
ln6
ln2
.
2) Comme
x0
, on a :
x53
ln x5
 ln3
5lnxln3
lnx1
5ln3
lnxln 31
5
x31
5
La solution est
31
5
.
Remarque :
31
5
se lit "racine cinquième de 3" et peut se noter
3
5
.