Exercice n°1: (4 points) Le transport du dioxygène vers les organes

CHIMIE :( 7points )
Exercice n°1: (4 points)
Le transport du dioxygène vers les organes s’effectue, sous forme de dioxygène O2 dissous dans le
sang des poumons, et sous forme d’oxyhémoglobine que l’on note HbO2. Celle-ci se forme lorsqu’une
hémoglobine du sang des poumons que l’on note Hb, fixe une molécule de dioxygène suivant la réaction
d’équation : Hb + O2 ; ; HbO2 (1)
1-Une quantité de sang arrive au niveau des organes qui absorbent le dioxygène dissous, faisant ainsi
chuter la concentration de ce gaz dans le sang. Le système chimique formé par l’hémoglobine, le
dioxygène dissous dans le sang et l’ oxyhémoglobine se trouve dans un état initial (i) tel que
[O2] = 3,6.10-5 mol.L-1 ; [Hb] = 2,8.10-4mol.L-1 et [HbO2] = 9,1.10-3 mol.L-1
a) Calculer la valeur de la fonction des concentrations i dans l’état (i), correspondant à l’équation (1).
b) La constante d’équilibre liée à cette équation est K1 = 3.105.
Déterminer le sens de l’évolution spontanée du système se trouvant à l’état (i).
2-Le monoxyde de carbone CO se trouvant dans l’air pollué, réagit avec l’hémoglobine suivant la
transformation chimique d’équation Hb + CO ; ; HbCO (2) et de constante d’équilibre K2 =
7,5.107.
a) L’analyse du sang d’une personne ayant respiré de l’air pollué par le monoxyde de carbone a donné
[CO] = 2.10-4 mol.L-1. Le tableau suivant donne les effets sur l’organisme associés aux valeurs du
rapport
Error!
à l’équilibre.
Indiquer, en le justifiant, les effets ressentis par cette personne.
b) Dans l’organisme, il ya compétition entre le dioxygène et le monoxyde de carbone pour se fixer sur
l’hémoglobine (équations (1) et (2)). On obtient un état d’équilibre correspondant à l’équation :
HbO2 + CO ; ; HbCO + O2 (3)
Etablir l’expression de la constante d’équilibre K3 associée à l’équation (3) en fonction de K1 et K2.
Calculer la valeur de la constante K3
c) Une personne empoisonnée au monoxyde de carbone, est placée dans un caisson dans lequel on
impose une concentration élevée en dioxygène, permettant ainsi d’augmenter la concentration de
dioxygène dissous dans le sang.
Expliquer qualitativement l’action du caisson.
Exercice n°2 :( 3 points)
L’ion hydrogénosulfate HSO4- réagit avec l’ion méthanoate HCOO- suivant la transformation d’équation :
HSO4- +HCOO- ; ; SO42- + HCOOH.
1-La constante d’équilibre de cette réaction est K = 64,5.
Comparer la force des acides mis en jeu par cette réaction.
2-Les couples HSO4- / SO42- et HCOOH/ HCOO- ont les pKa suivants : pKa1 = 1,94 et pKa2 = 3,75.
Attribuer à chacun de ces deux couples le pKa correspondant. Justifier la réponse.
3-Comparer la force des bases HCOO- et SO42- , d’après la valeur des constantes de basicité.
Error!
11.103 à 26.103
De 26.103 à 26.104
Supérieur à 26.104
Effets
Maux de tête
Intoxication grave
Mort rapide
Ministère de l’éducation
et de la formation
Direction régionale de
Nabeul
Lycée rue Taïeb M’hiri
Menzel Témime
DEVOIR DE CONTROE N°2
Classes:4èmes M1 et Sc.Exp2
Matière : Sc. Physiques
Profs : Abdelhakim. A
Samiya.T
Date : 29/1/2008  Durée : 2heures
Indications :
 Le sujet comporte 2 exercices de chimie et 2 exercices de physique.
 On exige l’expression littérale avant toute application numérique.
 L’usage des calculatrices non programmables est autorisé.

PHYSIQUE :( 13 points )
0
30
20
10
50
N(Hz)
I(mA)
70
90
(a)
(b)
(c)
Exercice n°1 :( 5,5 points)
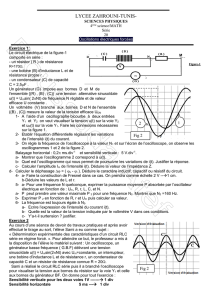
On relie les bornes A et B d’un condensateur de capacité C =0,25 F, respectivement à la borne positive
et à la borne négative d’un générateur de tension U0 = 6 V. Lorsque le condensateur se charge
complètement, on l’isole et on le branche à un instant t = 0s, aux bornes d’une bobine d’inductance
L = 1 H et de résistance considérée nulle.
1-Faire un schéma du circuit oscillant, sur lequel sont portés le fléchage du courant et des tensions,
uc= vA- vB aux bornes du condensateur, et ub aux bornes de la bobine.
2-Etablir l’équation différentielle régissant la tension uc.
3-La solution de cette équation est de la forme uc(t) = Um sin (
Error!
+)
a) Etablir l’expression de la période T0 des oscillations de la tension uc.
b) En déduire que cette période est propre au circuit.
4-a) Montrer que uc(t) = 6 sin (2000 t +
Error!
) .
b) Tracer dans l’intervalle [0 ;2T0], le chronogramme de la tension uc. On donne l’échelle : en abscisse,
1carreau pour
Error!
et en ordonnée,1 carreau pour 3V.
Exercice n°2 :( 7,5 points)
Un élève dispose du matériel suivant :
*Un générateur délivrant une tension sinusoïdale d’amplitude Um, constante et de fréquence N réglable ;
*Un condensateur de capacité C, un résistor de résistance R, une bobine purement inductive,
d’inductance L et un oscilloscope bicourbe.
L’élève monte en série le générateur, le condensateur, la bobine et le résistor. Il branche l’oscilloscope
pour visualiser la tension aux bornes du générateur à la voie Y1, et la tension aux bornes du résistor à la
voie Y2.
1-Schématiser ce circuit et établir à l’aide d’un tracé clair ses connexions avec l’oscilloscope.
2- Expérience 1 : L’élève choisit l’inductance L = 1H, la capacité C = 5 F, la résistance R = 33 et fait
varier la fréquence N.
a) Pour la valeur N0 = 71 Hz de la fréquence N, il affirme
que le circuit est en résonance d’intensité.
Préciser l’observation à l’oscilloscope conduisant l’élève à
cette affirmation.
b) La courbe (a) de la figure ci contre correspondant à cette
expérience, décrit l’évolution de la valeur efficace I du courant
dans le circuit, en fonction de la fréquence N.
Vérifier que les valeurs de L et C sont en accord avec la
valeur N0 de la fréquence N.
c) Calculer l’amplitude Um de la tension aux bornes du
générateur.
3-L’élève étudie l’influence des paramètres R et L sur la
résonance d’intensité. Pour cela il réalise les expériences
suivantes :
Expérience 2 : En fixant l’inductance L à la valeur 1H, il
règle la résistance R à une valeur R1 et étudie l’évolution de la
valeur efficace I, en fonction de la fréquence N.
Expérience 3 : En fixant R à la valeur 33 , l’élève règle
l’inductance L à une valeur L1 et étudie l’évolution de la valeur
efficace I, en fonction de la fréquence N.
A la suite de ces deux expériences, il obtient les courbes (b) et (c) de la courbe ci-dessus.
a) Montrer que la courbe (b) correspond à l’expérience 2 et la courbe (c) correspond à l’expérience 3.
b) Déterminer graphiquement les valeurs R1 et L1.
4-a) Montrer qu’à la résonance d’intensité de l’expérience 3, le condensateur est en surtension.
b) Dire, en le justifiant sans aucun calcul, si à la résonance d’intensité de l’expérience 1, le
condensateur est en surtension ou non.