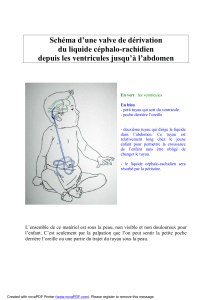
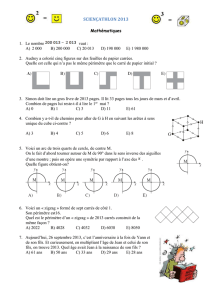
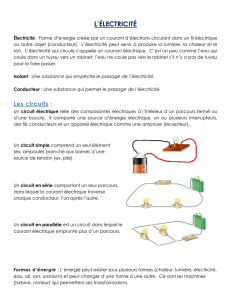
Etude d`une transformation chimique lente : réaction entre les ions

P a g e | 1
Tuyaux sonores Document : M.Moppert - CPF - Beyrouth
TS
Spécialité
Physique
Tuyaux sonores
Exercice
résolu
Enoncé
Donnée : la célérité du son dans l'air est v = 340 m.s-1 à 15 °C.
A. Première partie : ondes sonores
1. Une source sonore émet en continu un son dans l’air. Parmi les mots suivants, quels sont ceux qui
caractérisent une onde sonore qui se propage dans l'air : progressive, électromagnétique,
transversale, mécanique, longitudinale, stationnaire ?
2. Un auditeur peut déterminer la direction dans laquelle est située une source
sonore S, sans la voir, quand le retard entre les vibrations reçues par ses
deux oreilles D (droite) et G (gauche) est au moins égal à 1,0 x 10-4 s.
L'auditeur pourra-t-il définir la direction de la source sonore S si celle-ci est
située à 7,20 m de son oreille droite et à 7,10 m de son oreille gauche, la température étant
de 15 °C ?
B. Deuxième partie : tuyaux sonores à embouchure de flûte
Les tuyaux sonores à embouchure de flûte équipent en partie les tuyaux d'orgues. Un
tuyau sonore à embouchure de flûte comprend un biseau : l'air vient frapper ce biseau et il en
découle une mise en oscillation de la colonne d'air à l'intérieur du tuyau. Ces tuyaux sont
considérés comme des tuyaux ouverts au niveau de l'embouchure. L'autre extrémité du tuyau
peut être :
- soit ouverte, le tuyau sonore est alors un tuyau ouvert aux deux extrémités (à une extrémité
ouverte, est toujours situé un ventre de vibration noté V),
- soit fermée, le tuyau est alors ouvert à une extrémité, fermé à l'autre (à une extrémité fermée,
est toujours situé un nœud de vibration noté N).
1. Tuyau sonore ouvert aux deux extrémités
Un tuyau sonore de longueur L ouvert aux deux extrémités émet, à une température  = 15 °C, un
son de fréquence f = 262 Hz. L'état vibratoire est alors le mode fondamental. Il peut être
représenté de la manière suivante :
a) A quel type d'ondes appartient le mode de vibration de la colonne d'air ?
b) Parmi les trois caractéristiques suivantes d'un son, quelle est celle qui correspond à la fréquence f :
intensité, hauteur, timbre ?
c) Dans le cas d'une corde tendue entre deux points fixes, donner la relation entre la
distance d qui sépare deux ventres (ou deux nœuds) successifs et la longueur d'onde .
d) Sachant que cette relation reste valable dans le cas du tuyau sonore, en déduire la relation
entre L, v, et f.
e) A partir de la relation précédente, justifier l'affirmation suivante : « À un tuyau sonore
long correspond un son grave ».
f) Exprimer, en fonction de f, la longueur L2 du tuyau qui émettrait un son dont le fondamental
correspondrait à l'harmonique de rang 2 du tuyau de longueur L (tuyau dont l’harmonique de rang 1
est le mode fondamental). En déduire la relation entre L2 et L.
V
V
N

P a g e | 2
Tuyaux sonores Document : M.Moppert - CPF - Beyrouth
2. Tuyau sonore fermé à une extrémité
Soit un tuyau à embouchure de flûte de longueur L0, fermé à l'autre extrémité. Ce tuyau est
représenté ci-dessous dans le mode fondamental :
a) Par analogie avec une corde tendue entre deux points fixes, exprimer la fréquence f0 du mode
fondamental émis par ce tuyau en fonction de v et L0.
b) L’affirmation suivante est-elle vraie ou fausse : « Un tuyau ouvert aux deux extrémités sonne
avec une fréquence double de celle d'un tuyau de même longueur fermé à une extrémité » ?
3. Influence de la température sur la fréquence du son émis
Donnée :
- la vitesse du son dans l'air est proportionnelle à
T
(T est la température absolue, exprimée
en Kelvin (K) : T(K) = (°C) + 273,15
- le tuyau sonore étudié ici est celui de la question B.1
On réalise une nouvelle expérience au cours de laquelle la température de l'air a augmenté
de 7 °C : la célérité du son est devenue v' et sa fréquence f’.
a) Après avoir exprimé la célérité v du son dans l'air à la température absolue T puis la célérité v'
du son dans l'air à la température absolue T’, déduire l'expression de v' en fonction de T, T’ et v.
b) Montrer que la nouvelle fréquence f’ du son à la température T’ est donnée par la relation :
f’ =
T'
T
.f
c) Une oreille moyenne distingue deux sons de fréquence f et f’ si le rapport log
f'
f
est
supérieur à 5,0 x 10-3. L’oreille moyenne pourra-t-elle distinguer deux sons émis avec un écart de
température de 7,0°C ?
V
N

P a g e | 3
Tuyaux sonores Document : M.Moppert - CPF - Beyrouth
Corrigé
A. Première partie : ondes sonores
1. Une source sonore émet en continu un son dans l’air. Parmi les mots suivants, quels sont ceux qui caractérisent une
onde sonore qui se propage dans l'air : progressive, électromagnétique, transversale, mécanique, longitudinale,
stationnaire ?
Une onde sonore est une onde mécanique, progressive et longitudinale.
2. L'auditeur pourra-t-il définir la direction de la source sonore S si celle-ci est située à 7,20 m de son oreille
droite et à 7,10 m de son oreille gauche, la température étant de 15 °C ?
Soit t0 la date de début d’émission du son.
Soit t1 la date à laquelle le son parvient à l’oreille gauche après avoir parcouru la distance d1.
Soit t2 la date à laquelle le son parvient à l’oreille droite après avoir parcouru la distance d2.
On a : v =
1
10
d
tt
=
1
2
2
d
tt
. Or : t0 = 0 => v =
1
1
d
t
=
1
2
d
t
=>
1
1
d
tv
et t2 =
2
d
v
 est le retard de perception entre les deux oreilles : = t2 – t1 =
2
d
v
-
1
d
v
=> 
21
dd
v
Soit :  =
7,20 7,10
340
= 2,94 x 10-4 s
 > 1,0 x 10-4 s : l’auditeur peut définir le direction de la source sonore S.
B. Deuxième partie : tuyaux sonores à embouchure de flûte
1. Tuyau sonore ouvert aux deux extrémités
a) A quel type d'ondes appartient le mode de vibration de la colonne d'air ?
Dans la colonne d’air, il s’établit des ondes stationnaires.
b) Parmi les trois caractéristiques suivantes d'un son, quelle est celle qui correspond à la fréquence f : intensité, hauteur,
timbre ?
C’est la hauteur qui correspond à la fréquence f.
c) Dans le cas d'une corde tendue entre deux points fixes,
donner la relation entre la distance d qui sépare deux ventres
(ou deux nœuds) successifs et la longueur d'onde .
Deux ventres (ou deux nœuds) de vibration consécutifs
sont séparés par une demi-longueur d’onde : d =
2
d) Sachant que cette relation reste valable dans le cas du tuyau sonore, en déduire la relation entre L, v, et f.
Aux deux extrémités ouvertes on a des ventres de vibration. Dans le tuyau de longueur L, il y a
donc un nombre entier de demi-longueurs d’onde : L = n.
2
(n : entier positif)
Comme la colonne d’air vibre dans son mode fondamental (n = 1) : L =
2
Par ailleurs :  =
v
f
=> L =
v
2.f
e) A partir de la relation précédente, justifier l'affirmation suivante : « À un tuyau sonore long correspond un
son grave ».
D’après l’expression précédente, plus f diminue et plus L augmente : un son de plus basse
fréquence est perçu comme plus grave.

P a g e | 4
Tuyaux sonores Document : M.Moppert - CPF - Beyrouth
f) Exprimer, en fonction de f, la longueur L2 du tuyau qui émettrait un son dont le fondamental correspondrait à
l'harmonique de rang 2 du tuyau de longueur L (tuyau dont l’harmonique de rang 1 est le mode fondamental). En
déduire la relation entre L2 et L.
L’harmonique de rang 2 du tuyau de longueur L a pour fréquence f2 = 2f.
On aurait alors L2 =
2
v
2.f
(n = 1 : mode fondamental) => L2 =
v
4.f
et L2 =
L
2
2. Tuyau sonore fermé à une extrémité
a) Par analogie avec une corde tendue entre deux points fixes,
exprimer la fréquence f0 du mode fondamental émis par ce tuyau
en fonction de v et L0.
Pour une corde tendue entre 2 points fixes, la
distance entre un ventre et un nœud est d’ =
4
.
Pour le tuyau considéré : L0 =
4
(mode fondamental)
Par ailleurs :  =
v
f
. Donc, si on note f0 la fréquence du mode fondamental : L0 =
0
v
4.f
b) L’affirmation suivante est-elle vraie ou fausse : « Un tuyau ouvert aux deux extrémités sonne avec une
fréquence double de celle d'un tuyau de même longueur fermé à une extrémité » ?
Dans le mode fondamental :
- pour le tuyau ouvert aux deux extrémités : L =
v
2.f
(B.1.d)
- pour le tuyau fermé à une extrémité : L0 =
0
v
4.f
(B.2.a)
Si L = L0 =>
v
2.f
=
0
v
4.f
et f = 2.f0 : l’affirmation est vraie.
3. Influence de la température sur la fréquence du son émis
a) Après avoir exprimé la célérité v du son dans l'air à la température absolue T puis la célérité v' du son dans l'air
à la température absolue T’, déduire l'expression de v' en fonction de T, T’ et v.
v = k.
T
et v’ = k.
T'
=>
v
T
=
v'
T'
et v’ =
v. T
T
'
b) Montrer que la nouvelle fréquence f’ du son à la température T’ est donnée par la relation : f’ =
T'
T
.f
On a montré que v = 2.L.f. Comme la longueur du tuyau est la même : v’ = 2.L.f’
Or : v’ =
v. T
T
'
=> 2.L.f’ =
2.L.f. T
T
'
et f’ =
T'
T
.f
c) L’oreille moyenne pourra-t-elle distinguer deux sons émis avec un écart de température de 7°C ?
f'
f
1
2
T T'
T
T
'
=> log
f'
f
log
1
2
T'
T
=
1 T'
log
2T
 = 15°C => T = 288 K et ’ = 22°C => T’ = 295 K. Soit : log
f'
f
1 295
log
2 288
= 5,21 x 10-3
log
f'
f
> 5,0 x 10-3 : l’oreille peut distinguer les deux sons.
d’