sujet 13

Glissement sans frottement
Un palet, assimilé à un point matériel M de masse m, est lancé du point A avec la vitesse
 yA
Auvv
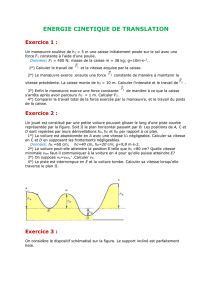
sur une piste où il glisse sans frottement. La piste est formée de la partie rectiligne AB de
longueur d et de la partie demi circulaire BC, de rayon r et de centre O, contenue dans le plan vertical de
AB. Si le palet atteint le point C, il continue son mouvement dans l'air et on négligera alors toute autre force
que son poids.
Pendant le mouvement circulaire on repère M par son élongation angulaire
  OM,OB
.
1) a) Exprimer l'énergie potentielle de pesanteur de M dans la partie circulaire de sa trajectoire,
avec m, g, r et θ, en prenant Ep = 0 quand M est en B.
b) En utilisant le théorème de l'énergie cinétique, exprimer le carré de la vitesse angulaire
2
avec vA, g, r et θ.
2) a) Démontrer que la réaction de la piste sur M, pendant le mouvement circulaire, s'écrit
  r
uNN
et exprimer dans la base
zr u,u,u
le poids de M avec m, g et θ ainsi que l'accélération de M
avec r et les dérivées temporelles de θ.
b) En déduire l'expression de N avec m, r, g, θ et , en appliquant la deuxième loi de newton,
puis avec vA, r, g et θ, en utilisant le résultat du 1) b).
3) Pour que M atteigne le point C, il faut que sa vitesse angulaire ne s'annule pas (sinon il revient en
arrière) et que la réaction de la piste ne s'annule pas (sinon le contact avec la piste est rompu).
a) Exprimer avec r et g la valeur minimale de vA pour que le palet ne revienne pas en arrière.
b) Exprimer avec r et g la valeur minimale de vA pour que le palet ne quitte pas la piste avant le
point C.
AB
C
D
O
r
θ
x
y
M
r
u
u
AB
C
D
O
r
θ
x
y
M
r
u
u

4) On suppose que le palet a bien atteint le point C.
a) Quelle est alors la valeur minimale de vC, exprimée avec r et g.
b) En prenant t = 0 à l'instant où M est en C, exprimer les coordonnées x et y de M en fonction
de t, avec les paramètres vC, r et g pendant son mouvement après le point C.
c) En déduire l'ordonnée du point D où M revient sur la droite AB, exprimée avec vC, r et g.
5) On veut que le palet revienne exactement au point A (D confondu avec A).
a) Quelle doit être la valeur minimale de la distance d = AB pour que cela soit possible ?
b) Quelle doit être la valeur de vA exprimée avec d, g et r ?
c) On donne r = 1,000 m et g = 9,81 m.s–2.
Calculer numériquement la valeur minimale que l'on doit donner à d ainsi que la valeur minimale
que l'on doit donner à vA.
d) Quelle doit être la valeur numérique de vA si d = 4,000 m ?