La courbe d`étalonnage. - Sciences physiques et chimiques

GT accompagnement personnalisé PC académie de Versailles
FICHE DE PRESENTATION DE L’ACTIVITE
Accompagnement personnalisé
Compétence(s) travaillées :
Micro-compétences associées :
Mobiliser
Construire et utiliser une courbe d’étalonnage
Titre de
l’activité :
La courbe d’étalonnage
Contexte dans
lequel
s’inscrit
l’activité :
Comprendre le principe, tracer et exploiter une courbe d’étalonnage.
Conditions de
mise en
œuvre :
Effectif : 16 élèves
Durée : 3h
Prérequis : tracés et exploitation de fonctions en maths
Disciplines concernées : maths, physique chimie
Autres : Ce document peut être travaillé avec des élèves de seconde ou de terminale. Pour les élèves de
seconde, on insistera d’avantage sur les premières activités. Pour les élèves de Terminales, les premières
activités serviront de remise en route et on portera l’effort sur l’exploitation de l’équation de la droite ainsi
que l’élaboration de la définition de la courbe d’étalonnage.
Déroulement de la séquence :
- Une activité découverte en mathématiques
- Exploitations graphiques de deux courbes d’étalonnage (courbe et droite)
- Construction et exploitation d’une courbe d’étalonnage (droite)
- Application au phénomène de diffraction : exploitation directe (graphique) et indirecte
(passage de la courbe à une droite et exploitation de son équation)
Document destinés aux élèves : pages 6 à 8

GT accompagnement personnalisé PC académie de Versailles
Document professeur
La courbe d’étalonnage : Principe et exploitation
1ère séance (1h)
Séances préliminaires de mathématiques
Approche mathématique de la modélisation des fonctions pour modéliser des problèmes non affines
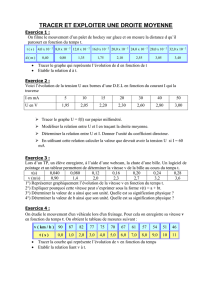
Exercice pour la séance
On souhaite utiliser une fonction affine pour modéliser le prix de revient unitaire d'un caisson de protection
pour des appareils scientifiques.
L'entreprise qui les fabrique, précise que le prix de revient théorique de fabrication se répartit en b euros de
frais fixes et a euros par unité produite, soit b+na pour n unités.
1. Exprimer en fonction du nombre n d'unités produites le prix de revient théorique y d'une unité
2. Dans la pratique, l'entreprise a relevé les résultats suivants :
Nombre d'unités :
ni
1
2
3
4
5
6
7
8
9
10
Prix unitaire
yi en euros
1504
809
540
438
375
320
290
254
231
212
3. Représenter ce tableau par un nuage de points (ni ; yi), (Abscisse : 1 cm pour 1 unité ; ordonnée : 1 cm
pour 100 euros. Peut-on considérer que les points obtenus sont proches d'une droite ?
4. On pose xi=1/ni
Calculer les valeurs des xi à 10-2 près par défaut, puis représenter le nuage (xi ; yi) sur le même schéma (1 cm
pour 0,1 unité).
5. Les points semblent mieux se répartir autour d'une droite, déterminer une équation réduite d'une droite
possible.
6. En déduire les coefficients a et b et le coût unitaire pour la production de 50 caissons.

GT accompagnement personnalisé PC académie de Versailles
2ème séance (1h)
Séance de physique
COMPRENDRE LA COURBE D’ETALONNAGE
I. Révélation(s) d’une courbe (35 min)
Exemple 1 : « Chute verticale d’une balle lâchée dans l’air sans vitesse initiale »
On se demande quelle est la durée d’une chute d’une hauteur de 1m50.
Ne connaissant pas l’équation du mouvement, on peut effectuer des mesures et construire un graphe pour
répondre à la question. On dispose d’un chronomètre et d’un décamètre.
On mesure les durées t correspondant à des hauteurs de chute h différentes (tous les 50 cm).
On construit le graphe de la fonction h = f(t)
0
0,5
1
1,5
2
2,5
3
3,5
0 0,2 0,4 0,6 0,8
h = f(t)
h(m)
t(s)
0,55
Exploitation du graphe : la balle chute d’une hauteur de 1m50 en 0,55s

GT accompagnement personnalisé PC académie de Versailles
Exemple 2 : «Déplacement d’un véhicule»
On se demande quelle distance, un véhicule qui roule à vitesse constante, aura parcouru au bout d’une heure
et demie. On ne dispose que d’une montre et des bornes kilométriques disposées sur le bord de la route.
On note l’heure, chaque fois que le véhicule passe devant une borne (tous les 50 km).
On trace le graphe donnant les distances d parcourues en fonction des durées Δt nécessaires pour les
parcourir.
0
50
100
150
200
250
300
350
0 1 2 3 4
d=f(Δt)
d(km)
Δt(h)
120
1,5h=1h30
Exploitation du graphe : en 1h30, le véhicule aura parcouru 120 km

GT accompagnement personnalisé PC académie de Versailles
Exemple 3 :
«En TP, une classe doit utiliser un circuit électrique déjà câblé, mais il n’y a aucune indication sur la tension
à utiliser pour l’alimenter. La technicienne qui prépare le matériel pour le TP sait seulement que l’intensité
du courant devient dangereuse à partir de 60 mA.
Elle dispose du circuit, d’une alimentation stabilisée pouvant délivrer les tensions suivantes (1,5V ; 3V ;
4,5V ; 6V ; 9V et 12 V) et d’un ampèremètre.
On attend des élèves qu’ils se posent le problème de la sécurité et qu’ils proposent à la préparatrice de
mesurer les intensités pour les tensions possibles de l’alimentation en commençant par la plus faible afin de
tracer le graphe de la fonction U=f(I) pour déterminer la tension maximale à ne pas dépasser.
On leur donne ensuite le tableau de mesures
U(V)
1,5
3
4,5
6
9
12
I(mA)
18
38
57
75
113
150
0
20
40
60
80
100
120
140
160
0 5 10 15
1ntensité (mA)
Tension (V)
Série1
Exploitation du graphe: la tension aux bornes du circuit devra rester inférieure à U = 5 V
II. A la recherche du diamètre d’un cheveu
1. Le phénomène de diffraction de la lumière pourrait-il être utilisé pour mesurer le diamètre de mon
cheveu ? (20 min)
- Vidéo (le propose de rechercher une vidéo montrant une expérience de diffraction avec différents
fils calibrés).
On attend des élèves qu’ils proposent de mesurer la largeur L de la tache centrale obtenue pour chacun des
fils calibrés de diamètre d (le tableau des valeurs expérimentales leur sera donné au début de la séance
suivante).