2009-2010 Sadiki

1/
Collège Sadiki
Devoir de synthèse n° : 2
Sciences physiques
4ème : maths et Sc.Exp
Vendredi 6 -3-2010
Profs : Obey- Fkih et Cherchari
 On donnera l’expression littérale avant de passer à l’application numérique.
 L’utilisation de la calculatrice non programmable est autorisée.
 Numéroter les questions.
N.B : Toutes les solutions sont prises à 25°C, temperature à laquelle le produit ionique de l’eau pure est
Ke=10-14.
Exercice 1 : (2,5 pts) :
On dispose de trois
solutions aqueuses (S1), (S2) et (S3)
d’ammoniac ( de pH>8). L’ammoniac NH3
est une base faiblement ionisée
1)
a- Écrire l’équation de la réaction d’ionisation
de l’ammoniac dans l’eau.
b- Dresser le tableau d’avancement
volumique de la réaction, sachant que la
concentration molaire de la solution
obtenue est notée C.
c- Montrer que le pH d’une solution
d’ammoniac, de concentration molaire C
peut s’écrire sous la forme :
ae
1
pH (pK pK logC)
2
; avec pKa est
celui du couple NH4+/NH3.
2) Les mesures de pH des solutions (S1), (S2) et (S3) ont permis de tracer la courbe de la figure 1
Déterminer graphiquement l’équation de la fonction pH=f(logC) puis déduire le pKa du couple NH4+/NH3.
Exercice 2 : (4,5 pts) :
I-/ Au laboratoire de chimie, au collège Sadiki, Monsieur Mustapha (Laborantin) a
préparé deux solutions acides (S1) et (S2) renfermant respectivement un acide A1H et A2H, l’un est faible
l’autre est fort, mais il a oublié de coller l’étiquette correspondante sur chaque flacon. Pour identifier les
solutions on a prélevé un volume V=20 mL de chacune d’elles et on a mesuré son pH, on a trouvé pH1=2,9
pour (S1) et pH=2 pour (S2).
1- Calculer la quantité de matière d’ions H3O+ dans chaque prélèvement.
2- On a réalisé une dilution au dixième des prélèvements précédents de (S1) et (S2) on a obtenu
respectivement deux solutions S’1 et S’2 puis on répété la mesure de pH, on a trouvé pH’1=3,4 pour (S’1) et
pH’2=3 pour (S’2).
a- Calculer la quantité de matière d’ions H3O+ dans (S’1) et (S’2).
a- Comparer les quantités de matière d’ions H3O+ avant et après dilution puis identifier la solution d’acide
faible.
II-/
1- La solution d’acide faible, préparée précédemment, renferme de l’acide éthanoïque CH3COOH de
concentration molaire C, à partir de cette solution, qu’on notera (S), et par dilution, on désire préparer trois
solutions (Sa), (Sb) et (Sc) de même volume V’=50mL et de concentrations molaires respectives
aC
C5
;
bC
C10
et
cC
C20
. Pour préparer ces solutions, on dispose du matériel suivant :
- Deux pipettes à deux traits de jauge de 5 mL et de 10 mL.
- Une pipette graduée de 5 mL.
- Deux fioles jaugées de 50 mL et de 100 mL.
a- Montrer que le volume prélevé Vp de la solution (S) pour préparer (Sb) est
b
pC V'
VC
b- Décrire le mode opératoire qui nous permet de préparer la solution (Sb) à partir de la solution (S). Justifier
la verrerie utilisée.
2-
On donne le tableau de variation du taux d’avancement final ’f de la réaction de dissociation de l’acide
éthanoïque en fonction du volume prélevé Vp pour préparer les trois solutions (Sa), (Sb) et (Sc).
Chimie ( 7 points )
0
logC
0,11
-1
11,6
(S1)
-2
pH
(S2)
(S3)
0,61
1,11
-3
Fig 1

2/
a- Compléter le tableau.
b- Tracer le graphe qui représente log’f =f (logVp).
3-
a- Dresser le tableau d’avancement volumique de la
réaction de l’acide éthanoïque avec l’eau.
b- Établir l’expression du taux d’avancement final f de
la réaction de dissociation de l’acide éthanoïque en
fonction de Ka constante d’acidité du couple CH3COOH/
CH3COO- et C la concentration molaire de l’acide. (l’acide CH3COOH est faiblement ionisé).
c- Déduire l’expression de ’f taux d’avancement final de l’acide éthanoïque après dilution en fonction de Ka,
C, V’(volume de la solution diluée) et Vp( volume prélevé pour préparer la solution diluée).
d- Justifier théoriquement l’allure de la courbe
e- Sachant que le pKa du couple CH3COOH/ CH3COO- est égal à 4,8 , déterminer à partir du graphe tracé, la
concentration molaire de la solution initiale de l’acide éthanoïque.
Exercice 1 : (5 pts) :
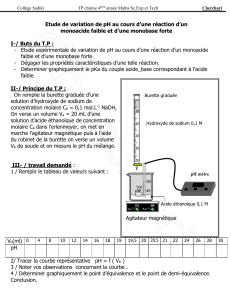
Partie A : Un solide (S) de masse m est attaché à l’une des
extrémités d’un ressort horizontal, parfaitement élastique, de constante de
raideur K et de masse négligeable devant celle du solide, l’autre extrémité
du ressort étant fixe (fig1). On étudie le mouvement du solide (S)
relativement à un repère galiléen (o,;i) horizontal, d’origine O coïncidant avec la position d’équilibre du
centre d’inertie du solide.
On écarte le solide (S) de sa position d’équilibre dans le
sens positif d’une distance Xm=3cm puis on le lâche sans
vitesse.
1-
a- En appliquant la relation fondamentale de la dynamique
au solide (S), montrer que son mouvement est rectiligne
sinusoïdal, de pulsation 0 qu’on donnera son expression
en fonction de K et m.
b- À un instant t quelconque, le centre d’inertie G de (S) a
une élongation x et sa vitesse instantanée est v. établir
l’expression de l’énergie mécanique E du système
S0={(S)+ressort} en fonction de x, v, K et m.
c- Montrer que l’énergie E est constante puis donner son
expression en fonction de K et Xm.
2- La solution de l’équation différentielle est x(t)=Xmsin(0t + ), déterminer l’expression de l’énergie
potentielle S0 en fonction K, Xm, 0, t et . Donner l’expression de sa période en fonction de K et m.
3- On donne la représentation graphique de l’énergie potentielle Ep (figure 2)en fonction du temps,
déduire :
a- La constante de raideur K du ressort et la période propre T0. Déduire la masse m du solide.
b- La loi horaire de mouvement du solide S
Partie B :
Dans cette partie, le solide (S) est soumis
à une force de frottement visqueux ;f=-
h;v ou h est une constante positive.
1- Établir l’équation différentielle de
mouvement du solide (S) régissant les
variations de son élongation x(t).
2- Montrer que l’énergie totale du système
S0={(S)+ressort} n’est pas conservée.
3- À l’aide d’un dispositif approprié, on a
enregistré les variations de l’élongation en
fonction du temps ; on a trouvé le graphe
de la figure 3 :
Calculer l’énergie dissipée par la force de
frottement entre les instants t1 et t2.
Physique ( 13 points )
Fig.
5
i
O
(S)
(R)
x
Fig 1
Solution
Sa
Sb
Sc
Vp(mL)
10
….
2,5
’f
0,028
0,040
0,056
logVp(mL)
….
….
….
log’f
….
….
….
0,075 s
t(s)
0
9
Ep(10-3 J)
Figure 2
0
-2
t(s)
1
2
3
x(cm)
t1
t2
Figure -3-

3/
Exercice 2 : (6 pts)
Un pendule élastique horizontal est formé :
- d’un solide (S) de centre d’inertie G et de masse m=0,2 Kg
- d’un ressort (R) à spires non jointives de masse négligeable et de
raideur K=100 N.m-1.
Le pendule repose sur un plan horizontal (figure 1) et la position du
centre d’inertie G du solide est repérée sur un axe horizontal (O,;i),
d’origine O position d’équilibre du solide. Au cours de son mouvement, le solide (S) est soumis à une force de
frottement visqueux ;f=-h;v (h=une constante positive). On soumet le solide (S) à une force
excitatrice ;F=Fmsin(t);i, d’amplitude Fm constante et de pulsation  réglable. À un instant de date t, on
notera x l’abscisse de G relative au repère (O,;i). On donne l’équation différentielle de mouvement du solide
(S) :
2
2
d x dx
m h Kx F(t)
dt
dt   
1) La figure 2 (page 4 à compléter et à remettre avec la copie) représente les courbes de variation de
F(t) et de v(t) : vitesse instantanée de G. Déterminer :
a- la pulsation  de l’excitateur.
b- Le déphasage de v(t) par rapport à F(t) =v -F, déduire le déphasage de la force F(t) par rapport à
x(t) F -x.
c- L’amplitude Xm des oscillations forcées de (S).
2)
a- Faire la construction de Fresnel relation à l’équation différentielle précédente (Ech :2N1cm).On
commencera par les vecteurs associés à Kx(t) et à F(t) puis on complètera la construction.
b- Déduire graphiquement h et m.
3)
a- Exprimer la dérivée de l’énergie mécanique E du système ={(S)+ressort} par rapport au temps en
fonction de F, v et f. A quelle condition cette énergie est constante.
b- Représenter sur le graphe de la figure 2, la courbe de variation de f(t) force de frottement (en utilisant la
même échelle que F(t)).
c- On notera T période de la force excitatrice F(t). sur l’intervalle de temps [0 ;T] indiquer en le
justifiant, l’intervalle de temps ouvert pour lequel E est décroissante.
4) En utilisant l’analogie électromécanique, donner :
a- L’expression de la puissance mécanique moyenne Pméc de l’oscillateur et calculer sa valeur.
b- Le schéma du circuit équivalent et dire si ce circuit est capacitif ou inductif.
Exercice n° 3 « document scientifique » (2 pts) :
Un objet vibrant effectue un va-et-vient de part et d'autre de sa position fixe normale. Un cycle complet de
vibration est produit lorsque l'objet se déplace d'une position extrême à l'autre position extrême, puis revient
au point de départ. Le nombre de cycles effectués par un objet vibrant pendant une seconde est appelé sa
fréquence.
Chaque objet, selon sa composition, sa taille, son poids…, a tendance à vibrer à une fréquence particulière.
Cette fréquence de vibration naturelle est appelée la fréquence de résonance. Une machine vibrante
transmet la quantité maximale d'énergie à un objet lorsqu'elle vibre à la fréquence de résonance de l'objet.
Lorsqu'une personne est en contact avec une machine vibrante, l'énergie de vibration est transmise à son
corps. Selon la durée et la façon dont l'exposition se produit, la vibration peut produire des effets sur une
grande partie du corps d'un travailleur ou seulement sur un organe particulier. Les effets de l'exposition aux
vibrations dépendent aussi de la fréquence de vibration. Chaque organe du corps a sa propre fréquence de
résonance. Lorsque l'exposition se produit à une des fréquences de résonance des organes ou au voisinage
d'une de ces fréquences, l'effet résultant sur les troubles de l'intestin et de l'appareil circulatoire, ainsi que des
systèmes musculo-squelettique et neurologique est grandement accru.
Centre canadien d'hygiène et de sécurité au travail
1- Comment est définie la fréquence d’un objet vibrant dans le texte ?
2- Quand est ce que l’énergie transférée de la machine vibrante à l’objet est maximale ?
3- Relever du texte les troubles provoqués par une exposition aux vibrations.
4- Relever du texte ce qui prouve que le danger de l’exposition aux vibrations est plus important lorsque
les organes se trouvent en état de résonance.
Fig.
5
i
O
(S)
(R)
x
Fig 1

4/
A compléter et à remettre avec la copie
Nom : …………………………………..……. Prénom : ……………………….. Classe : ……