sujet 4

Attention : dipôle magnétique et moment magnétique actuellement hors programme en MPSI.
Magnétostatique
1) Soit une spire circulaire de centre O, de rayon R, contenue dans le plan xOy, parcourue par un
courant stationnaire d'intensité I dans le sens indiqué sur la figure 1.
L'espace est rapporté au repère cartésien (Oxyz) de vecteurs unitaires
x
u
,
y
u
et
z
u
.
On notera P un point courant de la spire, repéré par ses coordonnées polaires (R,) dans le plan xOy,
et on notera
r
u
et
u
les vecteurs unitaires radial et orthoradial au point P.
z
M
y
figure 1
Pd
P
R
O 
N x
I
1-1) Quelle est la direction du champ magnétostatique
M
B
créé par la spire en un point M, de
coordonnées cartésiennes (0;0;z).
1-2) Exprimer le champ magnétostatique
M
B
avec 0, I, R, z et le vecteur unitaire nécessaire.
1-3) En déduire l'expression de
M
B
avec 0, I, R,  =
(MO
,
MP
) et le vecteur unitaire nécessaire .
Exprimer le champ magnétostatique
O
B
au point O.
2) On veut maintenant exprimer le champ
N
Bd
en un point N de Ox, de coordonnées cartésiennes
(x;0;0), l'abscisse x étant très petite devant R.
2-1) Quelle est la direction du champ magnétostatique
N
Bd
?
2-2) Exprimer le champ
N
Bd
créé en N par un petit élément de la spire
Pd
= R d
u
, avec 0, I, R, x,
, d et le vecteur unitaire nécessaire.
2-3) Effectuer un développement limité au deuxième ordre en
x
R
de
N
Bd
.
2-4) En déduire l'expression du champ
N
B
.
2-5) On peut mettre
N
B
sous la forme
N
B
=
0
B
(1+
ax
R
i
i
i
i
)
1
dans laquelle les coefficients ai sont des
fractions rationnelles.
Quelle est la valeur de a2 ? Quelles sont les valeurs des coefficients ai pour i impair ? (On utilisera
une symétrie pour répondre à cette question).

3) Un dipôle magnétostatique (petite aiguille aimantée), de moment magnétique
 z
u MM
est placé au
point N(x;0;0), voisin de O, (figure 2), dans le champ
B
créé par la spire, dont assimile la valeur à son
développement limité au troisième ordre en
x
R
.
y
figure 2 d
P
P
R
z O N
M
x
I
3-1) Quel est le moment du couple de forces exercé par la spire sur ce dipôle ?
Quelle est l'énergie potentielle d'interaction U entre la spire et ce dipôle ?
3-2) Exprimer la résultante
F
des forces exercées par la spire sur le dipôle, avec 0, M, I, R, x et le
vecteur unitaire convenable.
3-3) Lorsque le dipôle (gardant son moment magnétique dans la même orientation que précédemment) se
trouve en O, est-il en équilibre ?
S'il est alors en équilibre, cet équilibre est-il stable ? On répondra à cette question de deux façons
différentes :
- En utilisant l'expression de U trouvée au 3-1)
- En utilisant l'expression de
F
trouvée au 3-2).
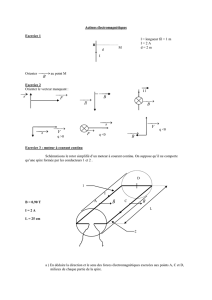
4) Sur une sphère de centre O, de rayon R, on enroule un fil conducteur, revêtu d'un vernis isolant, en
formant des spires pratiquement circulaires, de même axe Oz (de vecteur unitaire
z
u
). La distance entre les
plans de deux spires voisines est uniforme et très petite devant R. Le nombre total de spires est N. Un
courant stationnaire, d'intensité I, circule dans le fil, (figure 3).
Figure 3
z’
z
x
y
R
P
α
z’
z
x
y
R
P
α

4-1) Exprimer, avec N, R et dz, le nombre dN de spires sur une hauteur dz ?
On note P un point de la spire de cote z, et  = (
Oz'
,
OP
). Exprimer la relation entre dz et d avec
R, puis celle entre dN et d avec N et R.
4-2) Exprimer le moment magnétique d
M
de l'ensemble des spires de cotes comprises entre z et z+dz.
En déduire le moment magnétique total
M
de la bobine sphérique, exprimé avec R, N, I et
z
u
.
4-3) Exprimer le champ magnétostatique
O
Bd
créé au point O par la bobine de cote z, de hauteur dz.
En déduire le champ magnétostatique total
O
B
créé par la bobine sphérique au point O, exprimé
avec O, N, I, R et
z
u
.
4-4) Donner, sans démonstration, les expressions en coordonnées sphériques des coordonnées du champ
magnétostatique créé par la bobine sphérique en un point M(r,,) tel que r >> R. Ces coordonnées Br, B et
B seront exprimées avec O, N, I, R, r et .