Tp_11_Bobine

Nom
Bobines en régime sinusoïdal,
Circuits couplés
Classe Gr :
Date
TP n°:
Objectifs : . Déterminer le modèle équivalent d’une bobine avec et sans noyau de fer.
. Etude et détermination des caractéristiques de circuits couplés
Pré requis : . Cours sur les circuits magnétiques en alternatif
Conditions de réalisation :  Etude en régime sinusoïdal.
 Bobine sans fer, avec un noyau plein puis avec un noyau feuilleté. Suivre les
consignes de sécurité, les tensions dépassant parfois les valeurs de sécurité Utilisation de composants discrets
sous une tension inférieure à 24 V.
TRAVAIL DEMANDE :
I) Bobine sans fer:
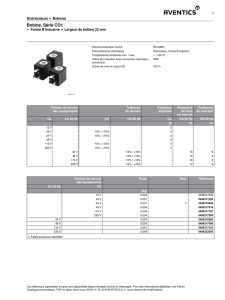
1) Déterminer la résistance de la bobine par la méthode voltampère métrique.
2) Alimenter la bobine sous tension sinusoïdale réglable. Faire varier l’intensité I de 0 à Imax = 1.5A.
3) Mesurer, pour différentes valeurs de la tension d’alimentation, U, I et P (puissance absorbée par la bobine).
4) Tracer U = f (I), en déduire l’impédance de cette bobine et son modèle équivalent série.
5) Déterminer le facteur de puissance de la bobine. Comparer P avec les pertes par effet Joule.
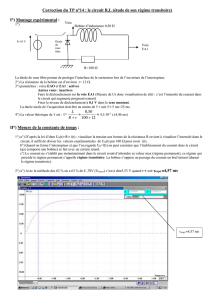
6) Relever les oscillogrammes de la tension u et du courant i. En déduire le facteur de puissance. Conclure.
II) Bobine à noyau de fer non feuilleté:
1) Relever les oscillogrammes de u et de i pour une tension de 20 puis de 200 V. Que remarquez vous ?
2) Relever les valeurs efficaces U et I. Tracer la courbe U = f (I) pour U variant de 0 à 200 V.
3) Comparer la puissance absorbée avec la puissance perdue par effet Joule. En déduire la puissance perdue dans
le fer.
Modèle équivalent :
Déterminer dans les deux cas (20 et 200 V) le modèle équivalent de la
bobine. Pour cela on tracera le diagramme de Fresnel en prenant U comme
référence des phases. On tracera U’ et on en déduira Ia , Ir puis Rf et L.
Autre méthode:
Pour calculer Rf , on négligera la chute de tension dans R (U  U’) et on
utilisera la valeur trouvée pour les pertes fer. On déterminera alors la puissance
réactive Q et on en déduira L puis Ia et Ir .
i
iair
u u'
L
Rf
R
Vérification: En utilisant les nombres complexes, déterminer la valeur littérale de l’impédance Z du circuit : en
déduire les valeurs de Rf et de L.
III) Bobine à noyau de fer feuilleté:
1) Refaire les mêmes mesures que précédemment : comparer les valeurs trouvées pour Rf et L pour les mêmes
tensions.
2) Comparer les puissances absorbées et les pertes fer : conclure.
IV) Circuits couplés:
On a deux bobines B1 et B2 concentriques, emboîtées l’une dans
l’autre.
Bobine extérieure B1 : 1200 spires ; Imax = 0,4 A ; R  100 .
Bobine intérieure B2 : 250 spires; Imax = 4 A ; R  0.4.
1) Mesure de l’inductance de chaque bobine :
Montage "a"
Montage "b"
Proposer une méthode et effectuer les mesures, les bobines ayant un noyau de fer.
Attention de ne pas dépasser le courant maximal admissible dans les bobines.
2) Mesure de l’inductance mutuelle :
Méthode directe : on n’alimente qu’une seule bobine et on en déduit M.
Méthode de Joubert : on détermine l’impédance et on en déduit M dans les deux cas proposés.
Manipulation: effectuer les mesures, déterminer M et comparer les résultats.