Lucie Morasse

[GÉOMÉTRIE ET ORIGAMI]
01 avril 2011
Commission scolaire des Navigateurs
Réalisé par Lucie Morasse, conseillère pédagogique en mathématiques
16/04/2017
1
Atelier de manipulations
En mathématiques
La beauté des figures régulières!
Premier cycle du secondaire

[GÉOMÉTRIE ET ORIGAMI]
01 avril 2011
Commission scolaire des Navigateurs
Réalisé par Lucie Morasse, conseillère pédagogique en mathématiques
16/04/2017
2
Description de l’activité pédagogique
1. Intentions d’apprentissage
 Amener l’élève à exploiter une feuille de papier pour construire des polygones
réguliers et différents solides.
 Amener l’élève à découvrir et à utiliser les propriétés géométriques des figures
planes pour construire des polygones réguliers et différents solides.
 Amener l’élève à développer des stratégies de résolution de problème.
 Développer ses habiletés sociales et intellectuelles dans le travail d’équipe.
2. Éléments ciblés du programme de formation (PFÉQ)
Compétence mathématique
CD1 – Résoudre une situation-problème
Amener l’élève à développer de nouvelles stratégies pour faire de nouveaux apprentissages.
Faire des liens avec les concepts et processus mathématiques. Collaborer avec les membres de
son équipe et partager à l’oral et à l’écrit les informations de sa démarche de résolution.
Concepts et processus mathématiques
Concepts :
 Triangles, polygones réguliers convexes,
bissectrice, médiatrice, hauteur,
orthocentre
 Angles
 Solides; pyramide, pyramide tronquée,
développement d’un solide, solide
décomposable
 Figures isométriques et semblables
 Relation d’Euler
Processus :
 Constructions géométriques
 Transformations géométriques : réflexion,
homothétie
 Longueurs : segments provenant d’une
similitude ou d’une isométrie
 Aires : aire de polygones décomposables
en triangles semblables ou isométriques,
aire latérale et totale de pyramides
droites
Domaines généraux de formation
 Orientation et entrepreneuriat
Compétences transversales
 Coopérer
 Communiquer de façon appropriée
 Faire une synthèse de ses connaissances
 Mettre en œuvre sa pensée créatrice
 Présenter sa démarche
 Utiliser du matériel de référence
Liens avec les autres disciplines
 Sciences et technologie
 Langue d’enseignement
 Univers social
Ressources
 Pairs
 Papier, colle, instruments de géométrie
 Consignes Enseignant
 Manuel ou lexique mathématique
3. Source
 Adapté d’un atelier de Joseph Georgeson, NCTM 2011, Indianapolis

[GÉOMÉTRIE ET ORIGAMI]
01 avril 2011
Commission scolaire des Navigateurs
Réalisé par Lucie Morasse, conseillère pédagogique en mathématiques
16/04/2017
3
Consignes à l’enseignant(e)
Déroulement de l’atelier :
1. Placer les élèves en équipe de 2 à 4.
2. Faire compléter aux élèves la feuille Annexe A, questions 1 à 9, avant de
travailler de distribuer les feuilles de couleur.
3. Une fois la feuille complétée, chaque élève prend une feuille rectangulaire
de papier de couleur différente.
4. Sans utiliser de règle à mesurer, demander-leur de plier la feuille
rectangulaire afin d’obtenir le plus grand triangle équilatéral en utilisant le
moins de plis possibles.
o Laisser-les les élèves chercher un certain temps et donner les indices
suivants s’ils ont de la difficulté.
 Créer l’axe de symétrie le plus long possible de votre feuille
rectangulaire.
 Créer un triangle dont un des sommets touche l’axe de
symétrie.
5. Ils suivent les consignes de l’atelier selon les différentes phases et vous
supervisez le travail des élèves.
6. Vous recueillez les solides afin de former l’icosaèdre et vous assemblez les
autres morceaux afin de faire d’autres solides réguliers. Vous pouvez aussi
le faire réaliser par les élèves.
7. Vous faites la correction de l’Annexe A à la fin de la période (si vous avez
du temps) ou comme retour sur les notions au cours suivant.

[GÉOMÉTRIE ET ORIGAMI]
01 avril 2011
Commission scolaire des Navigateurs
Réalisé par Lucie Morasse, conseillère pédagogique en mathématiques
16/04/2017
4
Consignes pour les élèves
Déroulement de l’atelier :
Phase 1
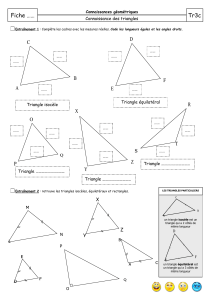
 En équipe, complétez les questions 1 à 9
sur la feuille « Annexe A », questions 1 à
9
 Allez chercher une feuille de couleur pour chaque équipier.
 Dessiner, sur la feuille rectangulaire, l’axe de symétrie le plus long
possible.
 Sans utiliser de règle à mesurer, plier la feuille rectangulaire afin d’obtenir
le plus grand triangle équilatéral en utilisant le moins de plis possibles.
 Créez un triangle dont un des sommets touche l’axe de symétrie.
 Indiquer le nombre de plis utilisés pour obtenir le triangle équilatéral.
Phase 2
 À l’aide d’une règle, mesurez et indiquez la longueur d’un des côtés du
triangle sur le papier.
 Mettez la règle de côté.
 Tracez au crayon de plomb les 3 hauteurs, les 3 bissectrices et les 3
médiatrices. Colorez une des trois hauteurs en jaune (surligneur).
 Indiquer d’un point de couleur ROUGE l’intersection des 3 hauteurs
(l’orthocentre).
 Inscrivez la mesure des 3 angles sur les deux triangles formés par le pliage
sur la hauteur colorée en jaune.
 Complétez la Phase 2 dans l’Annexe A.

[GÉOMÉTRIE ET ORIGAMI]
01 avril 2011
Commission scolaire des Navigateurs
Réalisé par Lucie Morasse, conseillère pédagogique en mathématiques
16/04/2017
5
Phase 3
 Indiquez la mesure d’une des hauteurs sur le triangle.
 Pliez le gros triangle de manière à obtenir une pyramide droite à base
triangulaire (tétraèdre)
 Repliez chacun des côtés de la pyramide sur la base pour obtenir un autre
triangle équilatéral plus petit. Pesez bien sur le papier pour que les plis
soient
 Indiquez (en bleu) la mesure du côté de ce nouveau triangle équilatéral sur
le papier.
 Dépliez les triangles obtenus et les mettre à plat.
 Tracez en bleu, le triangle formé par les plis des trois côtés.
 Pour chacun de ces nouveaux triangles, pliez le papier en allant déposer le
sommet du triangle sur l’orthocentre.
 Indiquez la mesure de chacun des côtés de la figure plane.
 Sans faire de nouveaux plis, superposez les trois plus petits triangles afin
d’obtenir une figure en trois dimensions.
 Avec du papier collant, solidifiez le solide.
 Complétez la Phase 3 de l’Annexe A
 Après avoir complétez toutes les questions de l’Annexe A, allez porter
votre solide à votre enseignant(e).
 Construisez le solide final avec les 20 premiers morceaux.