Travail, énergie, puissance

769780953 1/ 5
T
TR RA AV VA AI IL L, , E EN NE ER RG GI IE E, , P PU UI IS SS SA AN NC CE E
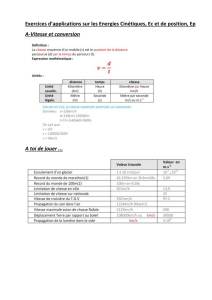
I. DEFINITION DU TRAVAIL
Le travail d’une force est défini par :
WF = Fd . d
Fd : composante de la force qui se trouve dans la direction du mouvement
d : distance parcourue en un temps t
Cas dans un mouvement angulaire :
d = r . α
donc, WF = Fd . r . α
WF = MF/o . α
Si on prend un couple de force F et F’ de sens opposés : F = F’
WF = Fd . r . α
WF’ = F’d . r . α
Wcouple = WF + WF’ = Fd . r . α + F’d . r . α = (Fd + F’d) (r . α)
= 2 Fd . r . α
= Mcouple . α
Le travail est en joules. Il existe une relation entre le joule et les calories (unités de
quantité de chaleur)
1 cal = 4,18 joules
1 C = 1 kcal = 4,18 KJ

769780953 2/ 5
II. ENERGIE MECANIQUE
Tout corps placé dans le champ de gravité terrestre possède une énergie potentielle :
Ep = m .g . h
Cette énergie potentielle va varier en fonction du travail du poids sur le corps en
mouvement.
Cette énergie va varier selon la hauteur. La variation de l’Ep correspond au travail de la
force de pesanteur sur le corps.
Tout corps en mouvement possède une énergie cinétique telle que :
Ec = ½ m . v²
Une variation de l’énergie cinétique mesure le travail qu’un corps peut effectuer de part
son mouvement. Ec = Ec0 + Σ WF
Si on prend un mouvement quelconque, le travail effectué sur un corps va être égal à :
W = ΔEc + ΔEp + Wft
Si on néglige les frottements sur un corps en mouvement rectiligne, la variation d’énergie
potentielle sera nulle, donc :
W = ½ m v² - ½ m v0²
Δ Ec = Σ WF
Dans un mouvement angulaire :
v = r . ω
Ec = ½ m v² = ½ m r² ω²
Ec = ½ (Σ m r²) ω² = ½ I ω²

769780953 3/ 5
On appelle énergie mécanique la somme de l’énergie potentielle et de l’énergie cinétique.
Em = Ep + Ec
Si on lance une balle, Ep augmente et Ec diminue jusqu’au point mort.
Quand elle redescend, Ep diminue et Ec augmente jusqu’au sol.
L’énergie potentielle est acquise par la balle lorsqu’elle monte et est reconvertie en énergie
cinétique lors de sa chute.
ΔEp = - Wp = P ( h – h0 ) (pendant la montée de la balle, la balle est soumise au
poids P qu’exerce une force négative)
ΔEp = - Wp = P ( h – h0 )
Ec = Ec0 + Wp = Ec0 - ΔEp
Ec = Ec0 - ( Ep - Ep0 )
Ec + Ep = Ec0 + Ep0
Si aucun travail n’est appliqué au corps pendant son mouvement, l’énergie mécanique
reste constante. Elle est conservée.
Si des forces sont appliquées au corps pendant le mouvement :
Em = Em0 + Σ WF appliquées pendant le mouvement
III. LA NOTION DE PUISSANCE
La puissance va introduire la notion de temps.
W P en watts (W)
P = W en joules (J)
t t en secondes (s)
W Fd . d
P = =
t t
donc, P = Fd . v

769780953 4/ 5
Pour un mouvement angulaire :
v = r . ω
P = Fd . r . ω P = MF/0 . ω
IV. LE TRAVAIL MUSCULAIRE
Une contraction musculaire entraîne un mouvement de rotation des segments par rapport à
une articulation. On distingue 2 types de travail musculaire : excentrique (allongement du
muscle) et concentrique (raccourcissement du muscle)
Contraction du biceps :
Mouvement de rotation de l’avant bras.
v : vitesse linéaire.
ω : vitesse angulaire.
F : force de contraction.
r : vecteur centre de rotation. Point d’application du muscle.
On sait que :
P = F . v et que v = r . ω
Donc P = F . r . ω avec F . r = M0 . F
Donc P = M0 . F . ω
Le sens du mouvement va nous donner le sens musculaire actif. Le sens de la vitesse
angulaire nous donne le sens de déplacement du segment.

769780953 5/ 5
4 possibilités :
Par définition : sens inverse d’une montre > 0 donc
Concentrique p > 0 P = M . ω
M et W > 0 M et W < 0
Concentrique fléchisseurs (biceps) concentriques extenseurs (triceps)
M > 0 et W < 0 M < 0 et W > 0
Excentrique fléchi excentrique extenseur