D6 – Comment la masse d`un astre peut-elle être calculée

D
D6 6 – – C Co om mm me en nt t l la a m ma as ss se e d d’ ’u un n a as st tr re e p pe eu ut t- -e el ll le e ê êt tr re e c ca al lc cu ul lé ée e
à
à p pa ar rt ti ir r d du u m mo ou uv ve em me en nt t d d’ ’u un n d de e s se es s s sa at te el ll li it te es s ? ?
Cette activité sur document vise à montrer comment, par application des lois de Newton sur le
mouvement et la gravitation, on peut déterminer la masse d’un astre. Elle fait appel à la
réflexion des élèves en les amenant à construire, puis à résoudre, un problème mettant en
œuvre aussi bien des capacités calculatoires et théoriques que des compétences relatives à la
mesure et à la détermination graphique d’une valeur. Pour cette raison, les élèves travaillent
en petits groupes de quatre sur des informations données sur document. Durant cette activité,
le professeur passe dans les groupes afin d’aider les élèves à résoudre les problèmes au fur et
à mesure qu’ils se posent. Aucune donnée générale n’est fournie dans le texte, mais les élèves
disposent d’un tableau de données concernant le système solaire et dans lequel ils pourront
tout aussi bien puiser les données qui leur sont nécessaires que trouver les valeurs qu’ils
pourront comparer à leurs résultats.
Le premier exercice, qui porte sur la détermination de la masse de la Terre, vise
essentiellement à poser le problème de la détermination de la masse d’un astre à partir des lois
de Newton, et donc à donner du sens aux activités qui vont suivre et qui concernent la planète
Jupiter et ses satellites. De plus, l’application à la Lune de la deuxième loi de Newton conduit
les élèves à s’interroger sur la relation donnant l’accélération du mouvement circulaire
uniforme. Cette relation (
/RVa 2
) pourra être introduite à cette occasion par le professeur.
Le résultat de ce calcul théorique sera ensuite transposé et réutilisé pour déterminer la masse
de Jupiter après qu’aura été résolu le problème de la détermination des caractéristiques du
mouvement de l’un de ses satellites (ici Ganymède).
Calcul de la masse de la Terre
La Lune tourne autour de la Terre sur une trajectoire sensiblement circulaire. Montrer
que, par application des lois de Newton, il est possible de calculer la masse de la Terre,
connaissant les valeurs caractéristiques du mouvement de la Lune.
En prenant les données nécessaires dans le tableau des données relatives au système
solaire fourni, calculer la valeur de cette masse.
À la fin de cette première partie, on indique aux élèves que cette méthode de calcul peut être
appliquée pour déterminer la masse de n’importe quel astre ayant un satellite en orbite
pratiquement circulaire, à condition de connaître le rayon et la période de son mouvement.
C’est le cas de Jupiter.
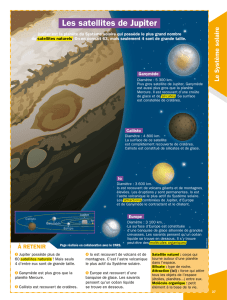
Les satellites galiléens de Jupiter vus de la Terre
Galilée a découvert en 1610 quatre satellites de Jupiter : Io,
Europe, Ganymède et Callisto.
En première approximation, on peut considérer que ces
satellites évoluent sur des trajectoires circulaires.
On pointe depuis la Terre une lunette astronomique centrée
sur Jupiter et on repère, à intervalles de temps réguliers, les
positions successives d’un de ces satellites. On reporte ces
positions sur le document ci-contre.
À votre avis, quelle sera l’allure du document que l’on
obtiendra ? (Tracez une dizaine de points qui vous
paraissent vraisemblables.)
Le ciel et Jupiter vus
dans la lunette

On peut s’attendre à ce que les élèves effectuent des prévisions du type de celles que nous
donnons ci-dessous.
On distribue alors aux élèves travaillant en petits groupes le document de la page suivante et
l’on pose les questions suivantes :
Ce document représente une série de photographies des satellites de Jupiter prises
depuis la Terre à des dates successives indiquées sous chacune d’elles. Sur ces
photographies, la position du satellite Ganymède est repérée par une flèche.
Ces photographies sont-elles en accord avec vos prévisions ? Quel renseignement vous
fournissent-elles sur le mouvement des satellites de Jupiter ?
Détermination du rayon de l’orbite et de la période de Ganymède
À l’époque où ces photographies ont été prises, la distance séparant les centres de la
Terre et de Jupiter valait environ 4,46 u.a. Montrez que, moyennant une hypothèse
simplificatrice, il est possible de déduire du mouvement apparent de ce satellite le rayon
R de son orbite et la période T de son mouvement autour de Jupiter.
Montrez que ces photographies permettent de calculer le rayon de l’orbite de Ganymède
ainsi que sa période de révolution autour de Jupiter. On s’interrogera en particulier sur
le choix de la méthode la plus précise.
Il s’agit ici d’amener les élèves à concevoir que, vu de la Terre, le mouvement d’un satellite
de Jupiter dans le référentiel centré sur Jupiter, est rectiligne, alternatif et périodique de
période T et d’amplitude pratiquement égale à R compte tenu de la faible valeur du diamètre
apparent de l’orbite du satellite vue depuis la Terre.
X’
X
S

La compréhension de ce mouvement apparent est essentielle pour pouvoir ensuite tirer profit
des informations que contient le document complet et qui permettent de déterminer la masse
de Jupiter.
Document de travail
L’échelle donnée en haut, à gauche est une échelle de diamètre apparent (4’ est l’angle sous
lequel les deux points A et B sont vus depuis la Terre).
Les élèves sont amenés à construire la courbe des abscisses apparentes des positions
successives de Ganymède en fonction du temps. On détermine alors graphiquement sur la
courbe la demi-période ainsi que l’amplitude du mouvement apparent à partir de laquelle on
calcule le rayon R de la trajectoire. Nous donnons ci-dessous les éléments de ces
déterminations.
A
B

On constate que la demi-période est d’environ
min100,5 3
soit une période
s1060T4
.
L’amplitude apparente est 27 mm soit un rayon apparent de 5,4’ et donc un rayon de l’orbite
de Ganymède
m101,1R 9
.
Détermination de la masse de Jupiter
Au moyen des résultats précédents, calculez maintenant la masse de Jupiter.
Le calcul donne :
kg101,9
T²
R
G
²4
M27
3
Données concernant le système solaire
Astre
Masse
relative à
celle de la
Terre
Rayon de
l’astre
(en 106 m)
Rayon
moyen de
l’orbite
(en u.a.)
Période de
rotation
(en 103s)
Période de
révolution
(en 106 s)
Mercure
0,0548
2,57
0,389
5,05x103
7,60
Vénus
0.807
6,31
0,724
21,0x103
19,4
Terre
1,00
6,38
1,000
86,1
31,6
Mars
0,107
3,43
1,524
88,5
59,4
Jupiter
319
71,8
5,200
35,4
374
Saturne
94,8
60,3
9,510
36,0
930
Uranus
14,7
26,7
19,18
38,8
2,66x103
Neptune
17,2
24,8
30,08
56,9
5,20 x103
Pluton
0,100
3
39,4
551
7,82 x103
Lune
0,0123
1,74
2,57 10-3
2,36
2,36 x103
Soleil
331
695
---
2,14
---
(
m1015.a.u1 10
)

Compétences scientifiques mises en œuvre
 Trier des informations ; extraire des informations pertinentes d’un tableau de valeurs
 Construire une courbe à partir d’un ensemble de mesures et savoir l’exploiter
 Utiliser un graphique pour déterminer une nouvelle grandeur
 Discuter la pertinence, la cohérence ou la logique d’une argumentation scientifique
 Utiliser les modèles et les lois pour prévoir des propriétés relatives à une situation donnée
 Utiliser des unités cohérentes
 Exprimer un résultat avec un nombre de chiffres significatifs compatible avec les
conditions de l’expérience
 Analyser des résultats expérimentaux, les confronter à des résultats théoriques.
Bibliographie
SANDRÉ, B. , « Détermination de la masse de Jupiter », Bulletin de l’Union des physiciens,
n° 732, vol. 85, mars 1991.