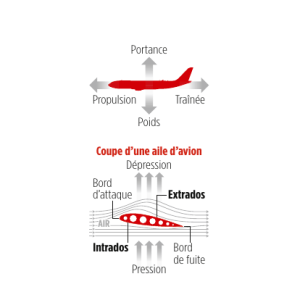
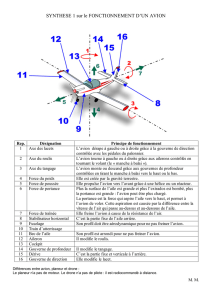
Bond sur la lune

Nom : Prénom : Classe : ( / 20 )
Comment faire atterrir un « Rafale » sur le Charles de gaulle ? (page 1 : 8 points)
On répondra directement sur le sujet (puis sur la copie avec le numéro de la question, si vous manquez de place).
I) Vitesse et énergie cinétique du porte avion
Le porte avion Charles-de-Gaulle peut aller à la vitesse de 27 nœuds (ce qui
correspond à 50 kilomètres par heure).Sa masse, en charge est de 40 000 tonnes.
1) Sachant qu’il existe une relation de proportionnalité entre la vitesse en km/h et
en noeuds, quelle est la valeur de 1,0 km/h en nœud ? (0,5)
2) Déterminer la valeur de l’énergie cinétique stockée par ce porte avion à cette
vitesse de 27 nœuds.
Donner cette valeur en utilisant le multiple le plus proche. (1,5)
II ) Appontage d’un « rafale »
Photo a) Le Rafale se présente à tribord du porte-
avions, à 200 m au dessus du pont d'envol. Cette
manoeuvre permet de vérifier que la crosse
d’appontage est bien sortie.
Photo b) Le Rafale peut être amené à vidanger son
excédent de carburant .
Photo c) Avec une incidence à 16°, le Rafale entre
dans l'axe du pont d'envol et est immobilisé en
quelques dizaines de mètres par le brin d'arrêt qu'il vient de saisir.
L'appontage est la fin d'une descente à pente constante qui se termine par un impact sur le pont. De jour, le
circuit d'arrivée s'effectue à bâbord à une altitude de 200 m. Pendant la phase vent arrière, le pilote « met au
poids » son appareil en fonction de sa configuration, larguant éventuellement du pétrole pour limiter la masse
totale du rafale à 15 *103 kg. En contact radio, les officiers d'appontage, situés tout en début de pont, lui
confirment que le train et la crosse sont sortis. L'alignement dans l'axe du pont d’envol précède la phase finale.
Informé par le miroir d'appontage sur sa position par rapport au plan de descente idéal, le pilote maintient
l'incidence et la vitesse à 130 noeuds (240 km/h, appelée vitesse de décrochage en dessous de laquelle l’avion ne
vole plus !), la poussée a alors pour valeur 1,0*105 N, elle est dirigée de P vers G, dans le sens de P vers G.
Echelle des distances : 1,0 cm représente 2,0 m ; intervalle de temps entre 2 photos consécutives : t = 32 ms
1) Montrer que la vitesse d’appontage est ici supérieure à 240 km/h, dans le référentiel terrestre. (2)
2) Dessiner un diagramme d’interaction pour le système {avion}, sachant qu’un des «objets en interaction» est
constitué par les gaz d’échappement qui pousse l’avion. (0,5)
3) Décrire le mouvement de l’avion dans le référentiel terrestre. (0,5)
4) Représenter qualitativement sur le dessin 3 (ci-dessus) les vecteurs force, puis donner leurs valeurs, après avoir
réalisé dans le rectangle en pointillé (ci-dessous) une résolution graphique.
Argumenter à partir d’une des lois de Newton.
Remarques : Echelle des vecteurs force imposée : 1,0 cm représente 1,0*105 N
Le dernier vecteur force, de point d’application inconnu, sera arbitrairement appliqué en G.
On prendra comme valeur de l’intensité de pesanteur g = 10 N/kg. (3)
G1
P
Dessin 2
G4
G2
G6
G9
P
Crosse d’appontage
Sens du mouvement
= 16 °
Dessin 3
G
PG P

Nom : Prénom : Classe : (page 2 : 12 points)
Le sujet sera rendu avec la copie !
Attraper un des trois brins d'arrêt,(la précision est de 20 m) est ensuite une manoeuvre réservée à l'élite.
Au moment du toucher, ignorant à cet instant si un des trois câbles a été saisi par la crosse d'appontage, le pilote
remet pleins gaz pour assurer le redécollage en bout de pont en cas d'échec.
Ce n'est que lorsqu'il est projeté vers l'avant par la retenue du brin d'arrêt qu'il coupe la puissance des réacteurs (en
quelques fractions de seconde, les gaz d’échappement ne poussent plus l’avion, l’atterrissage peut commencer !)
Un arrêt complet et brutal a lieu en 3,0 secondes, alors que la vitesse initiale est de 240 km/h.
La piste d’atterrissage a une pente de 8° par
rapport à la direction horizontale. Les pistons de frein, baignants d’un côté dans un liquide, reliés au câble de
freinage par l’intermédiaire de poulies, sont destinés à stopper des avions « Rafale » arrivant à 240 km/h sur 95 m.
5) Déterminer la différence d’altitude z entre le point I (brin accroché, moteur arrêté) et F (arrêt complet) (0,75)
6) Pour simplifier l’étude, on considère que l’avion est assimilable à un rectangle, que l’action de l’air est négligeable,
que la force exercée par le câble de freinage a la même direction que la piste d’atterrissage du Charles de Gaulle et
que les frottements exercées sur les pneumatiques sont négligeables devant toutes les autres forces (ce qui revient à
supposer que cette force de frottement n’existe pas).
a) Dessiner un diagramme d’interaction pour le système {avion}. (0,5)
b) Donner les expressions littérales des différents travaux (le signe et le qualificatif utilisé) des forces intervenant dans
ce diagramme (on ne demande pas de valeurs). Argumenter. (2,5)
c) Déterminer la valeur de la force exercée par le câble de freinage, supposée constante.
Pour cela, on utilisera le théorème de l’énergie cinétique (ou de l’énergie mécanique, la notation sera alors majorée
d’un point) qu’on énoncera, et après avoir dessiné un diagramme de transfert d’énergie correspondant (entre le point I
et F), on donnera une expression littérale de la force exercée par le câble de freinage. (4)
7) Déterminer la puissance exercée par le système de freinage pour un arrêt complet du rafale dans ce cas. (0,5)
8) QCM (/2,5) vous devez justifier rapidement votre réponse (sauf pour la question Q0).
Q0 : Le piston de l’amortisseur à poulie bâbord se déplace vers :
la droite
la gauche (0,25)
Q1 : Pour ralentir sur une plus courte distance, le Rafale doit se déplacer dans le même sens que le porte avion :
Vrai
Faux
cela n’a aucun rapport (0,75)
Q2 : En larguant du kérosène, le Rafale pourra ralentir sur une plus courte distance :
Vrai
Faux
cela n’a aucun rapport (0,75)
Q3 : Il est intéressant que la piste soit inclinée (et non horizontale), on peut ainsi ralentir le Rafale sur une plus courte distance :
Vrai
Faux
cela n’a aucun rapport (0,75)
Q4 : Si dans le cas de la question 6) c) on traçait la variation d’énergie cinétique en fonction de la distance parcourue sur le pont à partir
du point I, on obtiendrait une courbe qui est :
croissante
décroissante (0,75)
une droite passant par l’origine
une droite ne passant pas par l’origine
autre qu’une droite
Q5 : Si dans le cas de la question 7) c), on trace les énergies cinétique, potentielle de pesanteur, mécanique au cours du temps : (0,75)
L’énergie cinétique, au cours du temps :
augmente
diminue
ne varie pas
L’énergie potentielle de pesanteur, au cours du temps :
augmente
diminue
ne varie pas
L’énergie mécanique, au cours du temps :
augmente
diminue
ne varie pas
Dessin 5
= 8 °
F
I
z = …
Dessin 4
Crosse d’appontage
Brin d’arrêt
Amortisseur à poulie tribord
Liquide peu compressible
Symbolisation de
la fixation à la
coque du Charles
de Gaulle
Dessin 6
= 8 °
I
G
z = …

Correction 30 mn prof ( / 20 ) (page 1 : 8 points)
I) Vitesse et énergie cinétique du porte avion
Le porte avion a la vitesse de 27 nœuds (ce qui correspond à 50 km h. Sa masse, en charge est de 40 000 tonnes.
1) Valeur de 1,0 km/h en nœud et vice versa ? 50 km/h = 27 noeuds soit 1,0 km/h = 0,54 noeuds
45 km/h = 25 noeuds soit 1,0 noeud = 1,8 km/h 1 mn (0,5)
2) Valeur de l’énergie cinétique stockée à cette vitesse.Valeur en utilisant le multiple le plus proche.
Ec (porte avion) = ½ mv² = 0,5 * 40000 *103 * (50/3,6)² = 3,9 *10 9 J = 3,9 GJ
Ec = ½ mv² = 0,5 * 40000 *103 * (45/3,6)² = 3,1 *10 9 J = 3,1 GJ 0,5 expression litt , 0,5 calcul 0,5 multiple 1mn (1,5)
II ) Appontage d’un « rafale »
masse totale du rafale à 15 *103 kg. vitesse : 240 km/h, poussée a alors pour valeur 1,0*105 N, sens de P vers G.
Echelle des distances : 1,0 cm représente 2,0 m ; intervalle de temps entre 2 photos consécutives : t = 32 ms
1) Montrer que la vitesse d’appontage est ici supérieure à 240 km/h, dans le référentiel terrestre. 3 mn (2)
vitesse instantanée = vitesse moyenne car mouvement rectiligne uniforme
Vm = G1G9 / 8 t = (10,0 * 2,0) / (8*32*10-3) = 78 m/s soit Vm = 78*3,6 = 2,8*102 km/h ou
Vm = G1G9 / 8 t = (10,0 * 2,0) / (8*35*10-3) = 71 m/s soit Vm = 71*3,6 = 2,6*102 km/h 0,5 exp litt , 0,5 echelle 0,5 calcul 0,5 km/h
2) Dessiner un diagramme d’interaction pour le système {avion}, sachant qu’un des «objets en interaction» est
constitué par les gaz d’échappement qui pousse l’avion. Interaction avec gaz, terre, air (0,5)
3) Décrire le mouvement de l’avion dans le référentiel terrestre. 1 mn (0,5)
Mvt rectiligne uniforme : distance entre 2 pts consécutifs reste identique au cours (du même) intervalle de temps.
4) Tracé des vecteurs : g = 10 N/kg P = m*g = 1,5*105 N (0,5) et L(P) =1,5 cm (représentation 0,25), vecteur noté par soulignement, on
connaît les caractéristiques du vecteur F gaz/r dont la norme est 1,0*105 N , L(F gaz/r) = 1,0 cm (rep 0,25) , 1 ère loi de Newton : mouvement
rectiligne uniforme, la résultante des forces est égale au vecteur nul : R = 0 (0,5) soit P + F air/ rafale + F gaz/rafale = 0 (0,5) (triangle) (0,5)
alors L(F air/ r) = 1,6 cm , F air/ r = 1,6*105 N (0,5)
Echelle vecteurs force imposée : 1,0 cm représente 1,0*105 N, dernier vecteur arbitrairement appliqué en G. 5 mn (3)
Un arrêt complet et brutal a lieu en 3,0 secondes, avec vitesse initiale est de 240 km/h. La piste d’atterrissage a une pente de 8°. Les pistons de
frein, reliés au câble de freinage, sont destinés à stopper des avions « Rafale » arrivant à 130 noeuds sur 95 m. (page 2 : 12 points)
5) Valeur différence d’altitude z = IF sin = 95 sin 8,0 ° = 13 m ou z = 97 sin 8,5° = 14 m 0,5 exp litt , 0,25 calcul 1 mn (0,75)
6) a) Dessiner un diagramme d’interaction pour le système {avion}. Interaction terre, piste, câble 1 mn (0,5)
b) Expressions littérales des différents travaux (signe et qualificatif utilisé) des forces. Argumenter. 4 mn (2,5)
piste : W (F piste/ rafale) = 0J (0,25) car comme le mvt a lieu sans frottement alors F piste/ rafale est perpendiculaire à la direction du
mouvement (0,25)
terre : W (P) = - mgz (0,25), travail résistant (0,25) car composante tangentielle dans le sens contraire du mvt, le travail du poids est
indépendant du chemin suivi mais ne dépend que de la différence d’altitude (ici elle augmente, le travail est résistant). (0,5) argument
câble : W (F câble/ rafale) = - F câble/ rafale * IF = - f * IF, (0,5) travail résistant (0,25) car composante tangentielle (qui correspond dans ce cas
à la totalité de la norme) dans le sens contraire du mvt . (0,25) argument
c) Déterminer la valeur de la force exercée par le câble de freinage, supposée constante. 6 mn (4)
Pour cela, on utilisera le théorème de l’énergie cinétique (ou de l’énergie mécanique, la notation
sera alors majorée d’un point) qu’on énoncera, énoncé : voir cours (0,5)
et après avoir dessiné un diagramme de transfert d’énergie (entre I et F), (1) (+0,5 si théo Em)
on donnera une expression littérale de la force exercée par le câble de freinage.
Epp(F) – Epp(I) = mgz(F) – mgz(I) = mg.z avec Epp(F) – Epp(I) < 0
Em(F) – Em(I) = W piste/Raf soit Ec(F) – Ec(I) + Epp(F) – Epp(I) = W piste / Raf
(1) exp litt théo (+0,5 si théo Em) -1/2 *m* V(I)² + mgz = - f*IF (0,5) exp litt de f
D’où f = (+ 1/2 *m* V(I)² - mg z )/ IF = (0,5*15*103*67² - 2,0*106) / 95 = 3,3*105 N
(1) calcul, résultat
7) Puissance du système de freinage pour un arrêt du rafale dans ce cas. 1 mn (0,5)
P = W piste / Raf / t = ( f *IF ) / t = = 3,3*105 *95 / 3,0 = 1,0*106 W = 1,0 MW
(0,25) exp litt (0,25) résultat
8) QCM (/2,5) vous devez justifier rapidement votre réponse (sauf pour la question Q0).
Q0 : Le piston de l’amortisseur à poulie bâbord se déplace vers la gauche (0,25)
Pour le reste 5 mn (0,25) choix (0,5) argument
Q1 : Pour ralentir sur une plus courte distance, le Rafale doit se déplacer dans le même sens (et même direction) que le porte avion : Vrai car la
vitesse instantanée par rapport au porte avion (changement de référentiel) sera plus faible
Q2 : En larguant du kérosène, le Rafale pourra ralentir sur une plus courte distance : Vrai , car f est ici proportionnelle à la masse
Q3 : Il est intéressant que la piste soit inclinée (et non horizontale), on peut ainsi ralentir le Rafale sur une plus courte distance : Vrai car le
poids travaille ici de façon résistante
Q4 : Si dans le cas de la question 7) c) on traçait la variation d’énergie cinétique en fonction de la distance parcourue sur le pont à partir du point
I, on obtiendrait une courbe qui est une droite décroissante ne passant pas par l’origine
Ec(G) - Ec(I) + mg IF sin = - f *IF soit Ec(G) = - (f + mg sin )*IF + Ec(I)
- (f + mg sin ) est le coeff directeur , Ec(I) l’origine de la droite
Q5 : Si dans le cas de la question 7) c), on trace les énergies cinétique, potentielle de pesanteur, mécanique au cours du temps :
L’énergie cinétique, au cours du temps : diminue car v ↓ quand t ↑
L’énergie potentielle de pesanteur, au cours du temps :augmente car z ↑ quand t ↑
L’énergie mécanique, au cours du temps : Em = Ec + Epp diminue car Ec↓ et Epp ↓ quand t ↑
= 16 °
PFgaz / avion
Fair /avion
= 16 °
Dessin 3
G
PG P
Fgaz / avion
Fair /avion
P
Ec (I) =
Ec (F) = 0J
W F piste/Raf
montée
Sol
Epp(I) = OJ
Epp(F)
Théorème de l’Em
{Rafale en interaction avec la terre}