Bases de la mécanique : Actions et forces

IMRT1 – Soutien en mécanique PAGE 1 sur 4
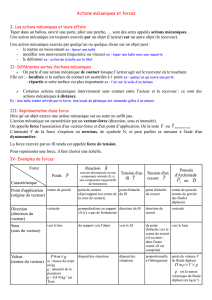
1. ACTIONS MECANIQUES – FORCES s’exerçant sur un système
Quand deux corps sont en interaction, ils exercent l’un sur l’autre des actions mécaniques ( AM ).
 Ex : la main qui appuie sur la table exerce une AM sur la table, mais la table
exerce également une AM sur la main.
1.1. Pour modéliser une action mécanique : le vecteur-force
Pour définir une action mécanique, il faut d’abord préciser quel corps est l’acteur ( c’est celui qui
exerce l’action, qui agit ) et quel est le receveur ( c’est celui qui subit ou reçoit l’action mécanique )
On peut représenter une action mécanique par un « vecteur-force » ;F (« flèche orientée »)
dont les caractéristiques sont les suivantes :
 la direction du vecteur est la même que celle de l’action
 le sens de l'action est le même que celui de l’action
 L’origine du vecteur-force correspond au point d'application de l’action mécanique.
 De nombreuses actions mécaniques ne sont pas localisées en un seul point ( ex : le poids
s’exerce sur tout le volume du corps ) ; on essaie cependant de les modéliser par une action
exercée en un seul point ( pour le poids, on considére qu’il est équivalent à une seule force
apliquée au centre de gravité du corps )
 La valeur F du vecteur-force correspond à l' intensité de cette force exprimée en
Newton (N).
 On mesure la valeur de la force avec des capteurs de force ( ex : des dynamomètres ) ou on
la calcule par des expressions théoriques ( ex : la valeur du poids est P = m.g ; g est
l’intensité du champ de pesanteur au lieu d’étude ) .
1.2. Le poids est une action mécanique
Le poids d’un corps est l’action mécanique d’attraction qu’exerce la terre sur ce corps.
Il peut être représenté par le vecteur-force poids
P
 direction : verticale
 sens : de haut en bas
 point d’application : centre de gravité du corps ( noté G )
 valeur : proportionnelle à la masse m du corps : P = m.g
 g est appelée intensité du champ de pesanteur et a pour valeur moyenne 9,8 N.kg-1
 La masse doit donc être exprimée en kg et le poids en N ( Newtons), unités du S.I.
1.2.a. Application :
Représenter le poids d’un oiseau de masse 500 g ( échelle 1 cm pour 1 N )
 quand il est posé sur le sol
 quand il est posé sur une branche
 quand il vole
1.3. Les différentes actions mécaniques
1.3.a. Actions mécaniques de contact
Ces actions mécaniques n’existent que s’il existe un contact entre les corps. Elles cessent
lorsqu’il n’y a plus de contact.
 Exemples d’actions mécaniques de contact exercées par :
 Un solide : action de contact du sol sur nos pieds
 Un liquide : action de contact de l’eau surla coque d’un bateau
 Un gaz : action de contact de l’ air sur notre figure ( impression de « vent » )
IMRT1 – 2007-08 soutien 10/12/2007 Bases de la mécanique

IMRT1 – Soutien en mécanique PAGE 2 sur 4
1.3.b. Actions mécaniques à distance
Ces actions mécaniques existent même en l’absence de contact entre les corps : elles peuvent
attirer ou repousser le corps.
 exemples d’actions mécaniques à distance :
 le poids ( attraction gravitationnelle de la terre sur les objets à sa surface )
 attraction ou répulsion électriques entre charges
 attraction ou répulsion magnétiques ( action d’un aimant sur un autre aimant ou sur une
charge en mouvement )
2. Le Diagramme objet-interactions et le bilan des actions mécaniques
2.1. Comment faire un bilan d’actions mécaniques ou bilan des
forces qui s’exercent sur un système ?
Il faut suivre la démarche suivante :
 Définir le système étudié .
 Définir le référentiel d’étude .
 Effectuer le diagramme objet-interactions ( D.O.I. ) de la façon suivante .
Le système étudié est le des AM.
Les autres objets agissant sur le système sont les . des AM
Lorsqu’il n’est pas nécessaire que l’acteur touche le receveur pour que
l’AM existe, on dit que l’action est exercée à distance et on utilise des
flèches en pointillés ( ) pour schématiser l’interaction. (
Exemple : action gravitationnelle exercée par la Terre sur une masse
à sa surface ).
Lorsqu’il est nécessaire que l’acteur touche le receveur pour que l’AM
existe, on dit que l’action est de contact et on utilise des flèches
pleines( ) pour schématiser l’AM ( ex : action de
contact du sol sur vos pieds ).
 Faire le bilan des actions mécaniques, en leur donnant un nom et une représentation
sous forme de vecteurs-forces ( Exemple : action gravitationnelle exercée par la
Terre sur tous les receveurs : le poids
P
) .
 Représenter sur le schéma chaque force connue, au moins partiellement
 Quand on ne connaît que la direction, le sens du vecteur-force, on le représente sur le
schéma avec une longueur arbitraire
 Quand on connait la direction, le sens et la valeur du vecteur-force, on le représente en
adoptant une échelle pour les valeurs des forces .
 Dans tous les autres cas, on ne représente pas le vecteur…car on risque de partir avec des
idéees fausses…
2.2. Applications :
1 - Effectuez les opérations présentées au 2-1 pour le système : { balle de tennis } aux différents
instants suivants:
o Quand la raquette frappe la balle
o Quand elle passe au dessus du filet
o Quand elle rebondit sur le sol
2- Deux petites boules de papier aluminium sont chargées
électriquement ( charges positives ) et suspendues à des fils
isolants qui leur permettent de garder leur charge ( l’ensemble
s’appelle un pendule électrostatique ) . On approche les
pendules l’un de l’autre sans que les boules puissent se toucher
.
receveur
acteurs
Boule
d’aluminium
Fil isolant
Potence

IMRT1 – Soutien en mécanique PAGE 3 sur 4
Pour chaque boule d’aluminium, effectuez les opérations présentées au 2-1
On admettra que l’action électrostatique des boules d’aluminium entre elles ont une direction
horizontale.
3. Lois de base de la mécanique newtonienne
3.1. Préalable : les référentiels galiléens
Quand on veut étudier un mouvement, il est indispensable de préciser le référentiel par
rapport auquel on l’observe.
 Par exemple : une personne assise dans une voiture qui se déplace est immobile par
rapport au référentiel{voiture}, alors qu’elle est en mouvement par rapport au
référentiel{route}.
Les lois de la mécanique classique ont été introduites par Isaac NEWTON, d’où le nom de
mécanique newtonienne.
Ces lois ne peuvent être appliquées que dans certains référentiels appelés référentiels
galiléens.
 Le référentiel terrestre sera considéré comme galiléen, même si certains faits
expérimentaux montrent qu’il ne l’est pas totalement.
 Un référentiel en mouvement par rapport à la terre ne peut être considéré comme galiléen
que si son mouvement est rectiligne ( trajectoire droite ) et uniforme ( vitesse constante )
La mécanique newtonienne est également mise en défaut pour des particules de très grande
vitesse ( vitesse supérieure au 1/10ème de la vitesse de la lumière ): on doit alors utiliser une théorie
différente, introduite par Albert EINSTEIN, qui est la mécanique relativiste .
3.2. Les deux premières lois de Newton
3.2.a. 1ère loi de Newton ou principe de l’inertie
Lorsqu’un système mécanique est soumis à un ensemble d’actions mécaniques
extérieures qui se compensent ( système pseudo-isolé ), alors le vecteur vitesse
G
V
de son
centre d’inertie G ne varie pas. La résultante des forces extérieures
0
ext G
F F V cte   
Réciproquement, si le vecteur vitesse
G
V
du centre d’inertie G d’un système mécanique ne
varie pas, alors l’ensemble des actions mécaniques extérieures appliquées au système se
compensent
0
G ext
V cte F F   
3.2.b. 2ème loi de Newton ou principe fondamental de la dynamique
Lorsqu’un système mécanique est soumis à un ensemble d’actions mécaniques
extérieures qui se compensent pas , alors son centre d’inertie G subit une accélération
G
a
telle que :
.
ext G
F F ma
 Dans ce cas, puisque le centre d’inertie du système subit une accdélération
G
a
, c’est que
son vecteur vitesse
G
V
n’est pas constant et varie ( le système accélère ou décélère )
3.3. Le travail d’une force le long d’un déplacement
3.3.a. Quand une force travaille-t-elle ?
Une force qui travaille provoque des effets visibles :
 Mise en mouvement , freinage
 Modification d’altitude
 Elévation de température
 Déformation temporaire ou définitive
 Donnez un exemple pour chacun de ces effets.

IMRT1 – Soutien en mécanique PAGE 4 sur 4
3.3.b. Expression du travail d’une force constante le long d’un
déplacement constant
Une force constante conserve la même direction le même sens et la même valeur au cours du
temps.
Pour caractériser l’effet d’une force constante
F
le long d’un déplacement rectiligne AB, on définit
le travail de la force le long du déplacement AB ( noté
BA
)F(W 
) de la manière suivante :
( ) . .cos( )
AB
W F F AB
 Le travail
BA
)F(W 
est une énergie et s’exprime en Joules ( symbole : J )
est l’angle entre la direction de
F
et la droite AB
Travail moteur : la force contribue au mouvement : -90 <  (°) < 90 , son travail est positif
Travail résistant : la force s’oppose au mouvement : (°) > 90 ou (°)< -90 , son travail est
négatif
Force ne travaillant pas ( perpendiculaire au mouvement ): (°) = 90 ou (°) = -90, , son
travail est nul
3.3.c. Travail du poids
Le travail du poids d’un corps est indépendant du chemin suivi par ce dernier et ne dépend que
des altitudes de départ et d’arrivée de son centre de masse G :
( ) .( )
AB
A B G G
W P mg z z
Remarque : lorsque le corps perd une altitude h , le travail du poids est
moteur
()W P mgh
AB 
lorsque le corps prend de l’altitude , le travail
du poids est résistant
()W P mgh
AB 
3.4. L’énergie cinétique d’un système
L’énergie cinétique d’un système est liée au mouvement de ce dernier. Plus il va vite , plus son
énergie cinétique est importante ( un vélo n’a pas la même énergie cinétique à 40 km/h qu’ à 60 km/h
). Plus le système a une masse importante, plus son énergie cinétique est importante ( un semi-
remorque ou un vélo à 40 km/h n’ont pas la même énergie cinétique ).
Pour un système de masse m en translation à la vitesse v ou un système ponctuel en
mouvement quelconque, l’énergie cinétique du système est définie par
2
1..
2
C
E mv
G
vv
vitesse du solide ponctuel ou du centre de masse du solide non ponctuel
3.5. Le théorème de l’énergie cinétique
Dans un référentiel galiléen, la somme des travaux des forces extérieures appliquées à un
système le long d’un déplacement A-B, provoque une variation de son énergie cinétique telle que :
( ) ( )
BA
C C A B A B
E E W F W F
 Rq1 : Le travail est donc un mode de transfert de l’énergie d’un système : si celui-ci reçoit
du travail moteur , son énergie cinétique augmente, s’il reçoit un travail résistant , son
énergie cinétique diminue.
 Rq2 : cas particulier :si le système se déplace à vitesse constante
0 ( )
BA
C C A B
E E W F
. On en déduit que
tan 0 moteurs résis ts
WW
.
Globalement le système ne reçoit pas de travail .