module g 21

G21
e2c en yvelines Page 1 sur 11
MATHEMATIQUES
TRONC COMMUN NIVEAU 2
MODULE G 21
Nom :
Date de distribution :
Prénom :
Date de validation :
Objectifs à atteindre :
Utiliser le rapporteur pour:
211 Mesurer des angles
212 Construire des angles
Modules pré requis :
TC15, TC24, G13 et G14

G21
e2c en yvelines Page 2 sur 11
Rappel sur la notion d’angle
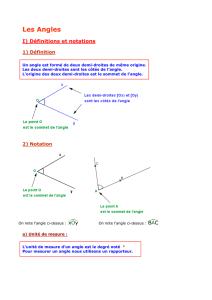
► Qu'est ce qu'un angle ?
Cette paire de ciseaux est à moitié ouverte. Des lignes prolongent l'ouverture des ciseaux.
En mathématiques, l'ouverture est appelée «angle» .
Plus l'ouverture est grande et plus la valeur de l'angle est grande.
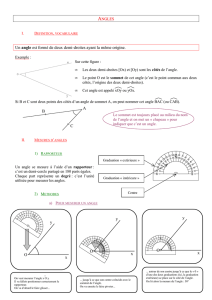
Deux demi-droites [O x ) et [O y ) de même origine O déterminent deux angles de sommet O
et de côtés [O x ) et [O y ) .
Soit A un point de l’une des demi-droites et B un point de l'autre :
A [O x ) et B [O y ) .
 L'angle qui contient le segment [AB] est saillant. Il se note AOB ou xOy.
 L'autre est rentrant. Il se note AOB ou xOy.
Remarques :
- On utilise et on mesure généralement l’angle saillant.
- la notation AOB et BOA désigne le même angle.
► Angle plat, droit, aigu, obtus
- Angle plat :
Les côtés d'un angle plat forment une droite .
Les côtés [ O u ) et [ O v ) de l'angle u O v forment la droite ( uv ).
L'angle « u O v est plat . Il mesure 180° .
On note : u O v = 180°.
u
v
O

G21
e2c en yvelines Page 3 sur 11
- Angle droit :
Un angle droit est la moitié d'un angle plat . Il mesure 90° .
On note : v O t = 90° .
On a aussi t O u = 90° .
- Angle aigu :
Un angle aigu est contenu dans un angle droit, il est plus petit qu'un angle droit.
On a : v O x < 90°
- Angle obtus :
Un angle obtus est compris entre un angle droit et un angle plat, il est plus grand
qu'un angle droit.
On a : v O x > 90°
Exercice 1 :
Nommer chaque angle, donner son sommet et ses côtés, et indiquer s’il est
aigu, obtus ou droit.
z
t
I
M
A
y
x
q
p
(3)
(2)
(1)
t
v
O
u
x
t
v
O
u
t
v
O
u
x

G21
e2c en yvelines Page 4 sur 11
Réponse :
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
211 Mesurer des angles
► Unités de mesure d’angle
Les unités utilisées pour mesurer un angle sont :
- Le degré : noté ° ,
il a pour sous-multiples : la minute notée ’, et la seconde notée ’’ .
- Le grade : noté gr ,
il a pour sous-multiples : le décigrade, le centigrade et le milligrade,
- Le radian : noté Rd ,
l'unité de mesure du radian est π ; il corresponde à 180° .
Remarques :
- Dans un cercle , il y a 360 degrés (2 angles plats) , ou 400 grades ou 2 π radians
( π = 3,14759...).
- 1° = 60’ et 1’ = 60’’, donc 1° = 3600’’.
► Présentation du rapporteur :
Un rapporteur est un demi-cercle sur lequel on peut lire des graduations d'angles
exprimées en degrés . Il y est indiqué un centre qui correspond au centre du
demi-cercle . Pour un demi-cercle, les graduations vont de 0 à 180 degrés.
Graduations

G21
e2c en yvelines Page 5 sur 11
► Mesure d'un angle
Remarque :
Mais si on devait graduer ce rapporteur en radians, elles iraient de 0 à π .
Conclusion :
À l'aide de cet outil, on peut mesurer et construire des angles.
Exemples :
- Dans l'exemple ci-dessous, l'angle mesuré est de 20° .
-
Sur le schéma représentant une pièce, il manque la valeur de l’ angle α (alpha) .
Christophe doit la mesurer afin de rentrer sa valeur dans une machine à
commande numérique. Comment place t-il le rapporteur ?
1ère phase :
Placer le centre du
rapporteur au sommet
O de l’angle.
2ème phase :
Placer la graduation
0° sur le 1er côté de
l’angle, ici Ox.
x
y
3
ème
phase : lecture de l’angle
La position du second segment,
ici O y , donne la valeur de
l’angle : 43° environ.
3 cm
3 cm
2 cm