Gérer la puissance et optimiser l`hélice

L'hélice
La « batteuse » constitue un système aérodynamique compliqué où des
compromis sont recherchés
Même à l'heure du réacteur, l'hélice reste un symbole quasi emblématique de l'aéronautique tout
entière. Déjà présente sur la machine de Clément Ader, elle n'en finit pas d'évoluer. Depuis le bois,
toujours présent, jusqu'aux composites les plus avancés, elle a connu de nombreuses évolutions
formelles qui, parfois, soulèvent l'interrogation des profanes et moins profanes. En dehors de son
aspect extrêmement esthétique, qui en fait la proie des collectionneurs, l'hélice est un élément qui a
pour raison d'être la transformation de la puissance mécanique, fournie par le moteur, en puissance
de propulsion. Sa forme lui permet de créer une accélération du débit d'air et une force dirigée vers
l'avant (cas général) que l'on nomme traction et qui, en vol horizontal stabilisé, équilibre la traînée de
l'avion. On pourra donc écrire que la puissance de propulsion est égale au produit de la vitesse propre
par la traction. Comme l'hélice est une machine qui transforme
une puissance mécanique, on ne peut l'aborder sans parler de
rendement. Le rendement va donc être le rapport puissance
restituée - puissance absorbée (Wa). L'on écrit : = T.Vp/Wa Un
rendement moyen d'hélice se situe autour de 0,8. Tout l'intérêt
d'un débat sur l'hélice est de connaître les facteurs propres à
augmenter le rendement de celle-ci. Décrivons d'abord le
fonctionnement de l'hélice dans ses grandes lignes...
Comme une aile
Si l'on isole une section de pale d'hélice, on obtiendra un profil
bidimensionnel comparable à celui d'une aile, c'est-à-dire doté
d'un bord d'attaque, d'un bord de fuite, d'une corde, d'une
épaisseur moyenne, etc. Comme pour l'aile, ce profil va déve-
lopper une résultante aérodynamique R, décomposable en deux
composantes : la première ne sera pas cette fois la portance mais
la traction T, l'autre sera une composante opposée à la rotation et
à l'origine d'un couple résistant. Mais, à la différence d'une aile,
les termes de portance et de traînée ne sont pas employés,
ceux-ci étant des vecteurs aérodynamiques perpendiculaires et
parallèles au vent relatif, ce qui, ici, n'est le cas qu'au point fixe.
D'autre part, l'incidence, donc l'angle entre le vecteur vitesse
relative Vr et la corde de la section, va varier à la fois en fonction
de la vitesse de rotation et de la vitesse sur trajectoire de l'avion.
On pourra dire que la vitesse relative Vr (parallèle et opposée au
vent relatif) de l'hélice est la somme vectorielle de la VP et de la
vitesse U (U = 2..r.N) avec r, le rayon, N le régime de rotation)
résultant de la rotation comme on le voit sur la figure 1. Le rapport
entre ces deux vitesses s'appelle paramètre de fonctionnement 
et l'on écrit  = VP/U
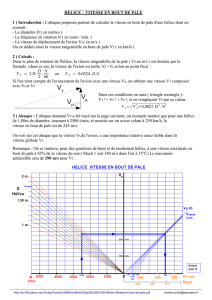
Sur la figure 2 représentant la section de référence au point fixe,
on voit que l'incidence (angle compris entre la corde et le vent
relatif Vr) est égale au calage (angle entre la corde et le plan de
rotation). A mesure que la vitesse va croître, le vecteur vitesse
relative Vr va pivoter, provoquant une diminution de l'incidence qui
deviendra inférieure au calage (fig. 1). Si l'on poursuit, au-delà
d'une certaine diminution de l'incidence, la résultante
aérodynamique sera confondue avec le plan de la pale (fig. 3). Le
couple résistant existera toujours, la traction sera nulle et en
conséquence le rendement aussi. Au delà (rotation de Vr au-delà
de la corde, incidence négative, fig. 4), la traction et le rendement
sont négatifs. C'est le moulinet, en cas de panne, le couple
moteur négatif fera cesser la rotation à basse vitesse mais, au contraire, à forte vitesse, c'est le vent

relatif qui fera tourner l'hélice, permettant par exemple un redémarrage sans usage du démarreur.
L'hélice aura alors une très forte traînée (de là vient la différence entre la finesse d'un avion hélice
calée et celle d'un avion hélice moulinant).
Quelques caractéristiques
Dans un premier temps, sans rentrer dans les détails du profil et de
la forme, on peut caractériser une hélice par son diamètre, son
nombre de pales et son pas (H). Commençons par parler de son
diamètre. Nous l'avons vu, la vitesse circonférencielle, en bout de
pale, dépend directement du rayon mais aussi de la vitesse
angulaire de l'arbre moteur. Pour la plupart des avions classiques
(moteurs tournants à 2 700 t/mn au maximum), les vitesses en
extrémité de pale sont de l'ordre de Mach 0,8 (Mach 0,78 au sol) et
leurs longueurs de pale sont quasi similaires. Toute augmentation
du diamètre aurait pour conséquence d'approcher un nombre de
Mach égal à 1 produisant une augmentation rapide de la traînée - et
donc une baisse du rendement -, d'éventuelles ondes de choc
générant des vibrations et, enfin, une augmentation du niveau
sonore, dont nous aurons l'occasion de reparler plus loin. Certains
moteurs, en aviation générale, ont des vitesses de rotation
supérieures à 5000 t/mn (Rotax par exemple), ce qui impose (sans réducteur) de réduire les
diamètres des hélices pour diminuer les vitesses en extrémité de pale. D'autre part, se pose le
problème tout à fait matériel de la garde au sol de l'hélice. Un grand diamètre imposerait un train
d'atterrissage gigantesque (citons au passage le Corsair, avion doté d'une très grande hélice et dont
le double dièdre des ailes représentait un compromis permettant de diminuer la hauteur du train).
Après avoir parlé du diamètre, on peut se poser la question du nombre de pales. L'hélice qui, dans
l'absolu, générerait le moins de traînée, serait une hélice monopale, mais cela nécessiterait un
contrepoids à l'opposé et serait irréalisable (même si des expériences ont vu le jour...), ainsi l'hélice
bipale s'est tout logiquement imposée. On pourrait, pour « passer »» plus de puissance, réaliser des
hélices de très grandes dimensions, mais nous ne pourrions éviter les problèmes du mach en bout de
pale et de la garde au sol. II ne reste donc que la solution d'augmenter le nombre de pales pour aug-
menter la traction. Ainsi sur des avions comme les Spitfire, le nombre de pales augmentait au rythme
de motorisations de plus en plus puissantes pour arriver, à la fin, à un système contrarotatif (doublet
d'hélices tournant en sens opposé) permettant de contrer un couple devenu hors limites. Cependant,
cette augmentation du nombre des pales a tendance à dégrader le rendement. On peut à ce sujet
faire le parallèle avec une aile d'avion sur laquelle, pour augmenter le coefficient de portance (Cz), on
augmenterait la surface alaire sans pouvoir augmenter l'envergure (allongement faible). On
augmenterait en conséquence le coefficient de traînée (Cx), et en particulier le Cx induit. Dans le cas
de l'hélice, c'est pire puisque l'on augmente la surface alaire en augmentant le nombre d'ailes dont les
traînées induites se suivent. Néanmoins, cette solution s'impose pour absorber la puissance avec un
diamètre donné. Après le diamètre et le nombre de pales, évoquons le pas. Si l'on considère l'hélice
sur le plan tridimensionnel, on constate qu'elle est vrillée. C'est-à-dire que l'angle de calage évolue,
diminuant vers l'extrémité de la pale. Ceci est purement lié à la vitesse circonférencielle de plus en
plus importante à mesure que l'on s'éloigne du moyeu. Ainsi, pour que, de façon théorique, toutes les
sections « avancent »» de la mème distance, le calage évolue au long de la pale. Cette distance, que
l'on peut comparer à la distance d'enfoncement dans l'air d'une vis sur un tour de 360°, s'appelle le
pas (H). Pas et calage () sont liés par une relation mathématique. H = 2..R.tang  (formule dite du
pas géométrique). On emploie souvent à tort l'expression d'hélice à pas fixe alors que le terme calage
convient mieux puisque le pas réel évolue, cela même sur une hélice à calage fixe. Le pas réel est, en
vol, inférieur au pas théorique (ou géométrique) du fait de l'incidence nécessaire à la traction. II ne
sera égal au pas théorique que lorsque l'hélice sera en transparence (traction et freinage nuls). On
peut d'ailleurs écrire comme définition du pas réel H'= VP/n
Comme ce calage varie, on détermine un calage nominal pour chaque hélice, généralement pris sur
une section de référence à 75 % du rayon maximal (on trouve parfois la valeur de 70 % dans des
ouvrages plus anciens, cette valeur étant une valeur française).
Gérer la puissance et optimiser l'hélice
Sur un avion à hélice à calage fixe, le régime d'hélice est directement lié au régime moteur. Lorsque le
régime est stable, la puissance motrice est égale à la puissance absorbée par l'hélice. Le calage sur

ces avions est généralement optimisé
pour la vitesse de croisière et son
régime. On l'observe d'ailleurs très bien
sur la courbe de variation du rendement
hélice en fonction de la vitesse propre VP
(fig. 5), assez comparable à une courbe
de performance humaine! Le rendement
maximum est obtenu pour une VP
optimale. Pour les VP inférieures à cette
vitesse, en montée notamment, l'hélice
absorbera trop de puissance moteur.
Celui-ci aura du mal à prendre tous ses
tours. A mesure que la vitesse propre va
augmenter, la puissance absorbée par
l'hélice va se stabiliser et le rendement
augmenter. Au contraire, pour les vitesses supérieures à celles de croisière, en piqué par exemple,
l'hélice absorbera une puissance inférieure à la puissance moteur et une réduction s'imposera afin de
ne pas emballer celui-ci. Après avoir évoqué les généralités, on peut se demander ce qui justifie tant
de formes différentes. L'hélice doit représenter un compromis entre des choix liés à la recherche du
meilleur comportement aérodynamique d'une part et le respect des contraintes mécaniques d'autre
part. Les contraintes aérodynamiques sont liées à la recherche du rendement optimal dans les phases
du vol les plus caractéristiques de l'avion. Une hélice à calage fixe ne sera pas la même pour un ap-
pareil destiné au remorquage de planeurs ou, au contraire, destiné à de la croisière rapide. Ainsi une
hélice optimale pour la montée, donc efficace à basse vitesse (composante VP faible), aura besoin
d'un grand diamètre (composante vitesse circonférencielle forte) pour obtenir une vitesse relative
optimale. Le calage le plus adapté sera un calage faible. La pale aura plutôt une longueur de corde
faible (analogie avec une aile à grand allongement). Une hélice optimale pour la croisière, donc
optimale à grande vitesse (composante VP forte), sera plutôt caractérisée par un petit diamètre
(composante vitesse circonférencielle faible). Le calage le plus adapté sera un calage fort avec
plusieurs pales ou une corde assez importante pour retrouver une surface suffisante (fig. 6). La figure
7 représente les différentes sections d'une
hélice en bois prévue pour un Rotax 912.
Le profit dissymétrique est convexe à
l'extrados, plat à l'intrados. Ce type de profil
permet un calage à l'intrados (profits de
type Clark). On observe l'évolution du
calage de plus en plus faible vers le bout
de pale, la diminution de l'épaisseur relative
et enfin de la courbure (ou cambrure).
Comme pour une aile d'avion, la courbure
et l'épaisseur relative sont capitales dans la
définition du profil et l'évolution de son
coefficient de portance (Cz). Le Cz variant
au cours du vol, la valeur voulue permet de
déterminer l'angle d'incidence du profil pour
un régime donné (régime de croisière par exemple). Cet angle d'incidence permettra de déduire un
angle de calage. II restera à choisir la cambrure qui, encore exactement comme sur une aile, est la
courbure moyenne exprimée en pourcentage de la corde. L'article de Paul Lucas, père du Dieselis
(Expérimental n° 56) fait état d'une relation très simple entre cambrure optimale et coefficient de
portance visé : la cambrure notée f/c = 0,1Cz ce qui donne, par exemple, pour un Cz de pale en
croisière de 0,35, une cambrure de 0,035, soit 3,5%. Ce n'est pas suffisant pour trouver le calage, il
faut connaître les caractéristiques du profil, et en particulier l'angle de portance nulle (0). Le même
auteur donne comme solution approchée, valable uniquement pour les profits de type Clark Y, de
prendre pour 0 la valeur de cambrure elle-même (0 = -f/c). La largeur de la pale, ou si l'on préfère
la longueur de corde, trouve à la fois une justification mécanique (résistance en pied de pale) et
aérodynamique (diminution de la traînée induite en bout de pale). Généralement, la corde est réduite
d'environ de moitié en extrémité. Chez l'hélicier Evra, par exemple, pour une hélice classique, on
applique la règle de 60% de la corde à 0,7R en bout de pale. La longueur de la corde et le traitement
du profit en pied de pale sont un autre sujet. II faut insister sur cette partie de la pale. Pour Richard
Evra, le problème est très différent entre un avion à large capot et prise d'air (Cessna 150, par

exemple) et un avion au capot profilé dans le prolongement du cône (MCR-01), sur lequel la pale
pourra offrir un meilleur rendement propulsif.
Des efforts à supporter
Les contraintes mécaniques résultent de la nécessité de résister
aux efforts appliqués. Une hélice en subit un certain nombre. Le
premier est l'effort centrifuge. Cet effort est proportionnel à la
masse, au rayon et au carré de la vitesse de rotation. II est
transmis en pied de pale, d'où la nécessité de travailler aussi
cette partie proche du moyeu. Le deuxième effort est un effort
de flexion qui tendrait à fait fléchir la pale vers l'avant pour une
hélice tractive (charge de l'hélice). Mais l'effort de flexion est en
partie compensé par la force de réaction aérodynamique liée à
l'avancée de l'avion. L'effort centrifuge qui, nous l'avons vu, est
proportionnel à la masse, tend, par la répartition inégale des
masses entre bord d'attaque et bord de fuite, à créer un couple
de torsion tendant à faire diminuer le calage. Les
rapprochements de fréquences, flexion - torsion, sont parfois
générateurs de problèmes d'aéroélasticité... Au final, pour être
certifiée, l'hélice, élément vital, doit supporter quatre fois l'effort.
L'utilisation de moteurs tournant à des régimes élevés, la
nécessité de diminuer le niveau sonore et les nouveaux
procédés industriels (composites), ont fait apparaître de
nouveaux types d'hélices en aviation générale et dans le monde
de l'ULM. Ainsi, les formes en « cimeterre » ou avec des
extrémités de pales en flèche, sont là pour retarder les effets de
la compressibilité, exactement comme sur un avion volant aux
vitesses subsoniques (Mach 0,80). On observe aussi, sur des hélices plastiques de faible diamètre, tri
ou quadripales destinées à des ULM, des longueurs de corde très faibles visant à travailler l'al-
longement et à réduire la traînée induite de l'hélice. Cette caractéristique, alliée a des épaisseurs
relatives et masses faibles, a pu être obtenue grâce à la technologie des composites. Certaines
formes apparues sur des avions de transport à turbines ont aussi pour fonction de déphaser les
sources acoustiques. Leur développement a nécessité des calculs complexes, car elles ne sont pas
sans poser des problèmes structuraux dus au fait notamment de décalages par rapport à la fibre
neutre et aux effets d'aéroélasticité évoquée plus haut. Nous avons vu que des hélices de diamètre et
profils semblables pouvaient donner des performances différentes suivant leur calage choisi comme
un compromis correspondant au mieux à la vocation de l'aéronef. En conséquence, l'idéal serait de
disposer dune famille d'hélice adaptée à chaque phase du vol. Aussi, un prochain article parlera de
l'hélice à calage variable...
Lionel CHAUPRADE
Illustrations de l'auteur, photos F. Besse et auteur