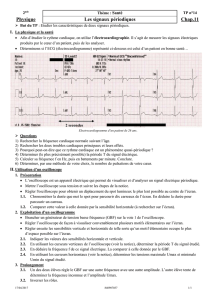
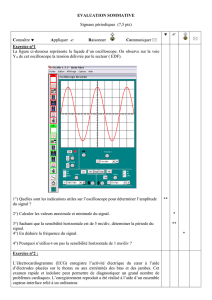
TP Physique Appliquée: Circuits et Analyse de Signaux

TP T STI Génie Electronique PHYSIQUE APPLIQUEE 1
[email protected] 769796391
Consignes générales pour tous les TP
1) Câbler un circuit électrique en respectant les consignes de sécurité :
- mise en service de l'alimentation électrique puis de la commande (GBF) après
vérification du montage (par les deux élèves puis par le professeur)
- coupure de la commande puis de l'alimentation (ou déconnexion) avant toute
intervention manuelle dans le circuit
- réalisation du circuit avant de brancher les appareils de mesure en dérivation (voltmètres,
oscilloscope)
2) Maîtriser l'emploi des appareils de mesure : ampèremètre, voltmètre, ohmmètre, multimètre,
oscilloscope :
- donner le résultat d'une mesure avec le maximum de chiffres significatifs compatible avec
les appareils utilisés
- prendre conscience :
- de l'impédance interne des appareils utilisés
- de l'influence de l'emplacement d'un appareil dans un montage
3) Relever de façon autonome les oscillogrammes en y faisant figurer : les grandeurs représentées,
les unités, les échelles et les coordonnées des points remarquables.
Remarque : code des couleurs (résistances à 5 %)
Noir : 0
Marron : 1
Rouge : 2 1er anneau : 1er chiffre significatif
Orange : 3
Jaune : 4 2ème anneau : 2ème chiffre significatif
Vert : 5
Bleu : 6 3ème anneau : multiplicateur (exposant de la puissance de 10)
Violet : 7
Gris : 8
Blanc : 9

TP T STI Génie Electronique PHYSIQUE APPLIQUEE 2
[email protected] 769796391
Liste des savoir-faire expérimentaux évaluables
pendant les séances de travaux pratiques
Manière d'effectuer les réglages :
respect du protocole de mise sous tension
R1
choix des fonctions et du calibrage des multimètres
R2
choix des fonctions et réglages du générateur basse fréquence
R3
réglages initiaux de l'oscilloscope :
mode d'utilisation (mono courbe, bicourbe, XY)
R4
inversion éventuelle des voies
R5
calibrage des amplificateurs de voies
R6
calibrage de la base de temps
R7
choix de la position du commutateur AC-DC
R8
choix de la voie de déclenchement
R9
stabilisation des courbes
R10
Techniques opératoires à connaître :
relevé de la courbe de gain en fonction de la fréquence d'un amplificateur, d'un
filtre
T1
relevé d'un oscillogramme avec indication des coordonnées des points
remarquables
T2
relevé de plus de deux oscillogrammes en concordance de temps
T3
mesure d'un déphasage par rapport à une grandeur de référence à l'aide d'un
oscilloscope
T4
visualisation d'une tension non référencée par rapport à la terre
T5
mesure d'une valeur efficace
T6
mesure d'une valeur moyenne
T7
mesure d'une fréquence de coupure à - 3dB
T8
mesure d'une durée à l'aide d'un oscilloscope (période, constante de temps, temps
de montée…)
T9
mesure d'un rapport cyclique à l'aide d'un oscilloscope
T10
en mode XY relevé du cyclogramme d’un comparateur
T11
détermination de l’excursion maximale du signal d’attaque permettant un
fonctionnement linéaire ; reconnaître une distorsion, un écrêtage
T12
à l’aide d’un système d’acquisition de données :
relevé du spectre d’un signal périodique
T13

TP T STI Génie Electronique PHYSIQUE APPLIQUEE 3
[email protected] 769796391
T.P. 1 : Circuits avec impédances complexes
Objectifs : - R1, R4, T2, T4, T8, T13
- exploiter une courbe de résonance :
- décrire par une phrase son allure,
- y placer la fréquence de résonance
- donner le résultat d'une mesure avec un nombre cohérent de chiffres significatifs
- utiliser un oscilloscope en mode XY pour repérer une concordance ou une opposition de phase.
A. Circuits R-L-C en régime sinusoïdal : résonance
1) résonance série : voir TP de 1ère
2) résonance parallèle (avec bobine imparfaite) :
LC
f
2
1
0
est la fréquence propre du circuit
Circuit à réaliser :
R A i
Rg = 50
(résistance de sortie)
R = 22 k Rg
L, rs C u
C = 176 nF
Eg
L = 1 mH GBF
M
rs à mesurer à l'ohmmètre
Le GBF ne doit pas délivrer de composante continue (offset nul)
a) Déterminer les paramètres (I0, R0) du modèle équivalent de Norton. du dipôle D de bornes A, M
constitué du GBF et du résistor R en série.
b) Après avoir calculé f0 et le coefficient de qualité QL de la bobine, déterminer, à la fréquence f0 ,
son modèle équivalent parallèle (Lp, rp)
c) Tracer le schéma équivalent du montage où tout est en dérivation aux bornes A, M .
Compte tenu des valeurs numériques, le dipôle D est pratiquement équivalent à une source de
courant de valeur efficace I0. Régler Eg = 6 V. Démontrer qu’on a alors I0 = 0,27 mA.
d) Relever la valeur efficace de u en fonction de la fréquence, pour des valeurs de f voisines du
maximum U0, à la fréquence f '0. ( f '0. est la fréquence pour laquelle U efficace est maximal)
Tracer la courbe de U en fonction de f. Comparer f0 et f '0. Comparer U0 et la valeur maximale
théorique de U.
Justifier, qu'à la fréquence de résonance, u et i sont en phase.
Décrire une méthode expérimentale qui permet de régler la fréquence à une valeur telle que u et
i soient en phase (oscilloscope en mode XY).
e) Déterminer les valeurs des fréquences de coupure fB et fH pour lesquelles on a
2
0
U
U
.
En déduire la valeur de la bande passante
f = fH - fB . La comparer à
0
0
Q
f
f) Déterminer, aux fréquences de coupure fB et fH , la phase de u par rapport à i
(relever les courbes)

TP T STI Génie Electronique PHYSIQUE APPLIQUEE 4
[email protected] 769796391
N.B. : rappel de la méthode de mesure du déphasage : phase de u par rapport à la phase de i
(pour une source de courant, il est logique de prendre i comme référence)
Ttt
rad 21
2)(
360
(deg)
(ici, t2 > t1 donc
-5,00
-4,00
-3,00
-2,00
-1,00
0,00
1,00
2,00
3,00
4,00
5,00
0 1 2 3 4 5 6 7 8
t (ms)
u1
u2
t1 quand i ou eg s'annule en
t2 quand u s'annule en
Oscillogramme n° 2
représentant eg et u à la
fréquence fH =
sensibilité :
Y1 : /div. DC/AC
Y2 : /div. DC/AC
X : /div.
Oscillogramme n° 1
représentant eg et u à la
fréquence fB =
sensibilité :
Y1 : /div. DC/AC
Y2 : /div. DC/AC
X : /div.

TP T STI Génie Electronique PHYSIQUE APPLIQUEE 5
B. Réponse du circuit sélectif à différentes formes de signal en entrée
Régler, en régime sinusoïdal, la fréquence du GBF à la valeur f '0. ( f '0. est la fréquence pour
laquelle U est maximal en valeur efficace)
Sans changer de fréquence, observer u(t) (forme, fréquence, amplitude) lorsque eg est
triangulaire, rectangulaire
Observer et relever u(t) lorsque eg est rectangulaire et que la fréquence est réglée à :
5
'
;
4
'
;
3
'
;
2
'0000 ffff
Que se passe-t-il en dehors de ces fréquences ?
Montrer qu’on peut dire que, si une tension est non sinusoïdale mais alternative et périodique de
fréquence fo, elle peut être décomposée en une somme de tensions sinusoïdales
Amplitudes des composantes de u
- de fréquence fo (fréquence fondamentale) et
- de fréquences 2fo, 3fo, 4fo,... (harmoniques)
f0 2f0 3f0 4f0 f
C. Bobine réelle. Pont d'impédance
E
Z1 = R = 10 k
Z4 = R' = 1 k
A
R3 Eg B V
Boites à décades
C3
f = 2 kHz
M
1) Calculer UAB en fonction de Eg et des quatre impédances du circuit
2) En déduire que, lorsque le pont est équilibré (quand UAB = 0), on a Z1.Z4 = Z2.Z3 (donc réel)
3) Quand le pont est équilibré, exprimer RX et LX en fonction des autres valeurs du pont.
4) Avec le composant inductif , ajuster R3 puis C3 pour que la tension efficace UAB soit minimale.
5) Déterminer la valeur du facteur de qualité du dipôle mesuré Z2
6) En déduire la structure série (rs , Ls ) du dipôle Z2
GBF
RX
R3
Z1
Z4
Z2
LX
C3
Z3
A l’oscilloscope :
spectre de u(t)
Menu MATH
FFT
 6
6
 7
7
 8
8
 9
9
 10
10
 11
11
 12
12
 13
13
 14
14
 15
15
 16
16
 17
17
 18
18
 19
19
 20
20
 21
21
 22
22
 23
23
 24
24
 25
25
 26
26
 27
27
 28
28
 29
29
 30
30
 31
31
 32
32
 33
33
 34
34
 35
35
 36
36
 37
37
 38
38
 39
39
 40
40
 41
41
 42
42
 43
43
 44
44
 45
45
 46
46
 47
47
 48
48
 49
49
 50
50
 51
51
 52
52
 53
53
 54
54
 55
55
 56
56
 57
57
 58
58
 59
59
1
/
59
100%