module 2 : analyse de variance a 2 facteurs avec

MODULE 2 : ANALYSE DE VARIANCE A 2 FACTEURS AVEC
REPETITIONS
Mise en pratique : corrigé
1) De quel type de dispositif expérimental s’agit-il ?
Il s’agit d’un dispositif à deux facteurs croisés, équirépété (r = 4)
2) Quelles questions l’expérimentateur a-t-il envisagées lors de la
conception de l’étude ?
Il cherche à savoir si la dose d’hormone influence le gain de poids, si le
gain de poids est influencé par le sexe du rat et si le sexe interagit avec la
dose d’hormone.
3) Représentez graphiquement l’étude, à l’aide du logiciel Excel.
Interprétez les graphiques obtenus.
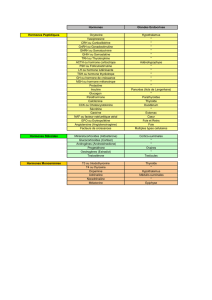
Influence de la dose d'hormone sur la croissance
du rat
120
125
130
135
140
145
dose d'hormone
poids (mg)
males
femelles
D1
D2
D3
Le gain de poids apparaît plus élevé chez les mâles pour les doses 1 et 3
seulement. L’écart observé entre les sexes dépend de la dose ; il est plus
important pour la dose 1 que pour les doses 2 et 3.
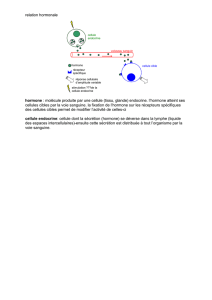
Effet de la dose d'hormone sur le poids du rat
120
125
130
135
140
145
sexe
poids moyen (mg)
D1
D2
D3
femelle
mâles
Les différences de gain de poids entre les doses d’hormone dépendent du
sexe de l’animal. La dose 1 est plus favorable pour les femelles, mais
moins favorable pour les mâles.

Il semble que le gain de poids soit influencé par les deux facteurs car
ceux-ci paraissent interagir.
4) Ecrivez le modèle qui va vous permettre de traiter les données et de
confirmer ou d’infirmer l’analyse graphique précédente.
yijk = ij + ijk
yijk : gain de poids mesuré sur le rat k de sexe i ayant reçu la dose i
Le modèle s’écrit aussi
yijk =  + i + j + ij + ijk
 moyenne générale
i : effet moyen du sexe i, i de 1 à 2
j : effet moyen de la dose d’hormone j, j de 1 à 3
ij : interaction entre le sexe i et la dose j
ijk : résidu (écart au modèle) pour l’individu k, k de 1 à 4
5) Calculez les valeurs prédites et les résidus estimés et vérifiez
graphiquement si les postulats du modèle linéaire sont vérifiés.
ijkijkijk
ijijk
yy
yy
ˆ
ˆ
ˆ.
sexe
hormone
poids
résidu
valeur
prédite
m
1
144
1,5
142,5
m
1
137
-5,5
142,5
m
1
151
8,5
142,5
m
1
138
-4,5
142,5
m
2
126
0,75
125,25
m
2
130
4,75
125,25
m
2
112
-13,25
125,25
m
2
133
7,75
125,25
m
3
133
-0,75
133,75
m
3
144
10,25
133,75
m
3
121
-12,75
133,75
m
3
137
3,25
133,75
f
1
129
4,5
124,5
f
1
112
-12,5
124,5
f
1
136
11,5
124,5
f
1
121
-3,5
124,5
f
2
134
-0,5
134,5
f
2
141
6,5
134,5
f
2
128
-6,5
134,5
f
2
135
0,5
134,5
f
3
136
10,5
125,5
f
3
116
-9,5
125,5
f
3
122
-3,5
125,5
f
3
128
2,5
125,5

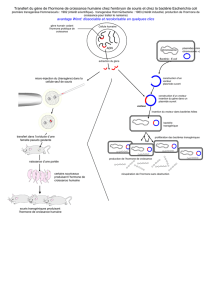
vérification des postulats : étude des résidus
-15
-10
-5
0
5
10
15
120 125 130 135 140 145
valeur prédite
résidu estimé
vérification de la normalité
-3
-2
-1
0
1
2
3
-15 -10 -5 0 5 10 15
résidu estimé
quantile N(0,1)
Le résultat du test de Levene est le suivant
Source de
variation
Degré de
liberté
Somme des
carrés
Carré moyen
F
Probabilité
associée
combinaison
5
49,71875
9,94375
0,503215604
0,769959744
résiduelle
18
355,6875
19,76041667
total
23
405,40625
La probabilité associée au F calculé est très supérieure à 0,05. On reste
sous H0. On n’a pas mis en évidence de différence entre les variances
résiduelles.
Les 4 postulats paraissent vérifiés. On peut analyser les résultats de
l’analyse de variance.
6) Construisez la table d’analyse de variance. Faites en l’interprétation
( = 5%) ; n’oubliez pas d’exprimer sous forme littérale vos
conclusions.
Source de
variation
Somme des
carrés
Degré
de
liberté
Carré
moyen
F
Probabilité
Valeur
critique
sexe
192,667
1
192,667
2,694
0,118
4,414
dose
d'hormone
75,250
2
37,625
0,526
0,600
3,555
Interaction
762,583
2
381,292
5,331
0,015
3,555
résiduelle
1287,500
18
71,528

Total
2318
23
L’interaction entre le facteur sexe et le facteur dose d’hormone est
significative. Les deux facteurs agissent sur le gain de poids. Les effets
moyens des deux facteurs sont non significatifs. Il faut tenir compte de
l’interaction pour interpréter correctement l’influence des facteurs.
7) Comparez ensuite les moyennes des trois doses ainsi que celles des
deux sexes. Les résultats sont-ils bien en accord avec la conclusion
précédente ? Confrontez les résultats à l’interprétation graphique
réalisée en premier lieu.
Etant donné qu’il existe une interaction significative entre les deux
facteurs, il faut comparer les moyennes des trois doses, pour chacun des
sexes et comparer les moyennes des deux sexes, dose par dose. Le
dispositif étant équirépété, chaque comparaison est réalisée avec le test
de Newman et Keuls.
Comparaison des 3 doses d’hormones
CMr
71,53
r
4
écart-type
moyenne
4,228770507
dlr
18
Q(3,18,0,95)
3,61
ppas
15,26586153
femelles
Dose1
124,5
Dose2
134,5
Dose3
125,5
d
134,5 - 124,5
10
< ppas
NS
D2 - D1
L’étude n’a pas mis en évidence de différence de gain de poids entre les
trois doses chez les femelles.
mâles
Dose1
142,5
Dose2
125,25
Dose3
133,75
d
142,5 - 125,25
17,25
> ppas
S
On continue avec des groupes de 2 moyennes
2
moyennes
Q(2,18,0.95)
2,97
ppas
12,55944841
D1 - D3
8,75
NS
D3 - D2
8,5
NS
Il existe des différences entre les 3 doses chez les mâles. La dose 1 induit
un gain de poids significativement différent de celui obtenu avec la dose 2.
D2 D3 D1D2 D3 D1

Le classement des doses varie selon le sexe étudié ; cela résulte d’une
interaction sexe x dose.
Les différences observées graphiquement ne sont pas toutes significatives.
C’est pourquoi l’analyse de variance doit compléter cette analyse
graphique.
Comparaison des deux sexes.
CMr
71,53
r
4
écart-type
moyenne
4,228770507
Q(2,18,0.95)
2,97
ppas
12,55944841
D1
D2
D3
males
142,5
125,25
133,75
femelles
124,5
134,5
125,5
ppas
12,55944841
pour D1
18
S
pour D2
9,25
NS
pour D3
8,25
NS
Seule la dose 1 induit des gains de poids significativement différents entre
les deux sexes. Les différences entre sexes dépendent bien de la dose
étudiée.