Charge et décarge d`un condensateur

viTüasßan bec©kviTüakm<úCa
kargarBiesaFn_ E3
Institut de Technologie du Cambodge
1-NOCH Vathana 3-NOEY Tre
3-NOP Long 4-NOP Vuthy
5-NORNG Kagnana 6-NORNG Satya Page 1
Charge et décarge d'un condensateur
I. Matériels nécessaire
- Oscilloscope
- Générateur de fonction
- Boite de résistances
- Condensateur 1µF
II. But
On observe les deux sugnaux sur la voix YA et la voix YB pour calculer les
amplitudes U et UC et la constante de temps  .
III.Charge et décharge d’un condensateur
A. Observation
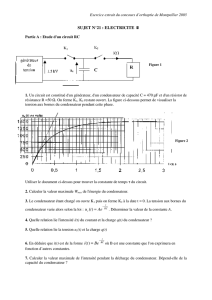
On considère le circuit R,C série ci-dessous R = 2000, C = 1µF. Le circuite est
alimente par un générateur de signal rectangulaire de grand période (50Hz).
B
Y
A
Y
C
U
R
U
I
U

viTüasßan bec©kviTüakm<úCa
kargarBiesaFn_ E3
Institut de Technologie du Cambodge
1-NOCH Vathana 3-NOEY Tre
3-NOP Long 4-NOP Vuthy
5-NORNG Kagnana 6-NORNG Satya Page 2
1./ Sur la voix YA, on observe la tension de condensateur UC.
Sur la voix YB, on observe la tension de générateur U.
2./ D’après (Fig 1) et Fig (2) on peut obtenir :
- Amplitude du signal délivré par le générateur :
2Um = SV.Y = 1V.5 = 5V
=> Um = 2,5V
- Amplitude du signal au bornes de condensateur :
2UC = 1V.5 = 5V
=> UC =2,5V
3./ On a : U = UR + UC
= Ri + UC mais i =
dt
dU
CC
U = R
dt
dU
CC
+UC
Suposant ’ = RC et U = constant a tε[0,T]
dt
dUC
+ Uc –U = 0
Uc – U = A
'
t
e
A t = 0, Uc = 0 => A = U
=> Uc = U(1-
'
t
e
)
Cette fonction mathématique est sous forme de Y=A
'
t
e
+ B.
Alors la fonction mathématique de la courbe (Fig 2) est aussi sous cette forme.
B. Etude théorique
1. Charge
Pour effectuer l’etude théorique on considère le circuit R,C série ci-dessous.
Lecircuit est alimenté par un générateur de courant continu de f-e-m E.

viTüasßan bec©kviTüakm<úCa
kargarBiesaFn_ E3
Institut de Technologie du Cambodge
1-NOCH Vathana 3-NOEY Tre
3-NOP Long 4-NOP Vuthy
5-NORNG Kagnana 6-NORNG Satya Page 3
0
dt
dq1
dt
dI 
A t = 0-, on considère que le condensateur n’est pas chargé. A t = 0, on ferme
l’intérrupteur.
1./ A t = 0 le condensateur est déchargé.
=>Qc = 0
mais UC = Q/C => UC(o) = 0
E = UR + UC
=> UR = E = 3V =>UR(o) = 3V
UR(o) = RIo => Io = 3/2000 = 15.10-4A
=> Io = 15.10-4A
2./ On a E = UR + Uc
E = RI +
C
q
0 = R
dt
dI
+
dt
dq
C
1
0 =
dt
dI
+
dt
dq
RC
1
avec  = RC
On en déduit I = k
t
e
B
Y
A
Y
C
U
R
U
I
U
E

viTüasßan bec©kviTüakm<úCa
kargarBiesaFn_ E3
Institut de Technologie du Cambodge
1-NOCH Vathana 3-NOEY Tre
3-NOP Long 4-NOP Vuthy
5-NORNG Kagnana 6-NORNG Satya Page 4
t
eII o
A t = 0 , Io = k
3./ Pour t =  => I = 0
I = C
dt
dUc
=> Uc =
dte
C
I
dt
C
It
t
C
t
0
Uc =
0
t
e
CIo t
Uc = E(1-
t
e
)
A t =  => UC() = E = 3V
Q() = CUC =10-6.3 = 3µC
Q() = 3µC
Comme à t = 0, Q = 0 et à t = , Q() = 3µC
On appelle ce phénomène charge du condensateur.
4./ Q = CU
Q(t) = CE(1-
t
e
)
Uc(t) = E(1-
t
e
)
On peut tracer l’allure de Uc (1)
Uc
E
t
O

viTüasßan bec©kviTüakm<úCa
kargarBiesaFn_ E3
Institut de Technologie du Cambodge
1-NOCH Vathana 3-NOEY Tre
3-NOP Long 4-NOP Vuthy
5-NORNG Kagnana 6-NORNG Satya Page 5
t Ee(t)UC
t ECeQ(t)
b./ Décharege
Au bout d’un temps très long par rapport au temps caractéristique, on annule E la
F-E-M du générateur. (C’est à dire qu’on remplace la générateur par un fil).
1./ UR + UC = 0
RI + UC = 0
RC
dt
dUc
+ UC = 0
dt
dUc
+
1
UC = 0 où  = RC
UC = k
t
e
(1)
à t = 0 => UC(o) = E
UC = E
t
e
Q(t) = CUC(t)
B
Y
A
Y
C
U
R
U
I