Introduction - Nathalie Rion

Montage n° 10
Expériences, à l'aide d'un dispositif à coussin d'air, sur la conservation de la
quantité de mouvement et sa variation dans quelques cas simples.
Introduction
Nous allons faire, au cours de ce montage, des expériences à l’aide de dispositifs à coussin
d’air. Leur particularité est qu’ils permettent l’étude du mouvement de systèmes pseudo-isolés,
c’est à dire de systèmes pour lesquels F=0. En effet, le poids du mobile est compensé par la
réaction R exercée par le coussin d’air et il n’y a pas de frottements. Dans ce montage, nous
allons étudier plus particulièrement la quantité de mouvement qui se définit par p=mv, sa
conservation et sa variation dans quelques cas simples.
D’après le principe d’inertie, un corps pseudo isolé dans est référentiel galiléen, est soit au
repos, soit animé par un mouvement rectiligne uniforme.
D’après le principe fondamental de la dynamique, . Donc si la quantité de
mouvement se conserve, alors , donc =0 (système pseudo isolé).
I. Conservation de la quantité de mouvement
I.1. Trajectoire d’un mobile
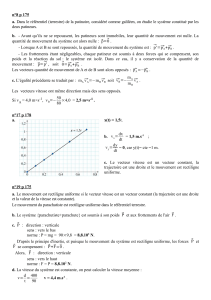
 v0=0 : mobile immobile (la table est bien réglée). Principe d’inertie vérifié.
 v0≠0 : mobile animé d’un mouvement de translation uniforme (principe d’inertie
vérifié)
Sur table à coussin d’air avec 2 mobiles autoporteurs munis de bagues élastiques.
T=40ms. On enregistre la trajectoire du choc. On exploite avant le choc pour un mobile.
Faire remarquer que mouvement rectiligne uniforme. D’ou conservation de p.
I.2. Principe du carreau
v1≠0 et v2=0
Sur banc magnum ( ?)
On place un chronomètre sur chacun des capteur qui mesure le temps de passage du
mobile dans la fourche du capteur. Après le choc, mobile 1 est immobile et c’est le 2 qui
acquiert de la vitesse.
t1=0,275s m1=94,3g t2=0,278s m2=89,4g d=8,5cm
v1=0,309 m.s-1 d’où p1=29,1 10-3 kg.m.s-1 et v’2=0,306 m.s-1 d’où p’2=27,4 10-3 kg.m.s-1
avant le choc, mouvement rectiligne uniforme pour le mobile 1 car il est pseudo isolé.
Après le choc, idem pour le mobile 2. Le mobile 1 est à l’arrêt.
On calcule p1, p’1=0, p2=0 et p’2 (dirigé selon v, selon la direction du banc).
Montrer qu’il y a conservation de p avant et p après le choc. C’est normal car =0
Rq : 6% d’erreur
I.3. Choc élastique
v01=0 et v02=0
Exploiter l’enregistrement précédent et montrer que avant le choc et après le choc, on a
conservation vectorielle de la quantité de mouvement. Faire une seule détermination de p
v1
v2=0
d

en direct. (avec webcam, PC et vidéo projecteur). Les 3 autres auront été faites en
préparation. Rq : 7% d’erreur
Il y a à peu près conservation de p. C’est normal car =0 (système = mobile 1 +
mobile 2 – c’est important de le mentionner !!!)
On peu s’amuser, s’il reste du temps, à calculer la trajectoire du centre d’inertie du
système. On vérifiera qu’elle est rectiligne uniforme. (principe d’inertie).
On peut vérifier aussi qu’il y a conservation de l’énergie cinétique car le choc est élastique
(ce qui n’est pas le cas dans les chocs mous).
II. Variation de la quantité de mouvement
II.1. accéléromètre
Sur banc magnum avec
acquisition des points
Le système n’est pas
pseudo-isolé : il est soumis à T=mg. Tracer v=f(t) et p=f(t). La pente de la dernière courbe
doit être égale à mg. La variation de la quantité de mouvement au cours du temps est
égale à la somme des forces extérieures appliquées au système.
II.2. plan incliné
Sur table à digitaliser.
ay=gsinα
px=mvx=cst
py=mvy=cst
projeter sur x et y et comparer à la théorie (PFD)
Conclusion
Tous ces exemples nous montrent bien que le principe fondamental de la dynamique est
vérifié. La quantité de mouvement est constante si le système est pseudo-isolé, et elle varie
dans le cas contraire.
Ce sont des expériences faciles à mettre en œuvre et à réutiliser dans les lycées.
BIBLIO
 [1] Bellier Dunod (p.153 ch8 : explication de la détermination de v et de a à partir d’un
relevé de points – choc élastique – plan incliné)
 [2] Duffait (p.211 : explication du fct de la table à digitaliser – choc élastique – choc non
élastique – II.1 bien expliqué)
 [3] Quaranta (p.337 – théorie bien détaillée)
QUESTIONS
1. Quand a-t’on conservation de la qdemvt ? quand le mobile est pseudo-isolé (non
soumis à des forces extérieures)
2. Choc élastique ? p et Ec se conservent
3. Choc inélastique ? p se conserve mais pas Ec !!! Exemple du choc de 2 mobiles avec
bande velcro : une partie de l’énergie cinétique sera transformée en déformation,
échauffement (chaleur). Une partie de l’énergie cinétique de translation peut aussi être
transformée en énergie cinétique de rotation. (de l’ensemble des 2 mobiles). Exemple de
choc inélastique : accident de voiture : il y a déformation, donc transfert d’Ec en chaleur.
4. Objets ponctuels : on néglige l’énergie de rotation du mobile sur lui-même (ce qui peut
expliquer les erreurs ???)
5. Fonctionnement de la prise de mesure sur le banc Magnum ? alternance de secteurs
transparents et noirs
m
α

6. Choc d’un camion (M) en mouvement (v0) avec un vélo (m<<M) au repos ? après le
choc, le vélo aura une vitesse égale à 2v0. Application : effet de la fronde spatiale pour
les sondes d’exploration spatiale : la sonde se sert de la vitesse de la grosse planète
pour prendre de la vitesse.
7. En l’absence de force, le mvt d’un mobile est rectiligne uniforme. Pourquoi ? ma=0.
En intégrant : v=cst.
8. 2 particules en mvt dans un plan. Après le choc, leur trajectoire est-elle tjs dans le
même plan ?