Influence d`une charge électrique ponctuelle sur la surface plane d

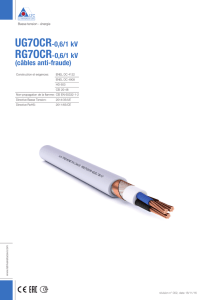
Influence d’une charge électrique ponctuelle sur la surface plane d’un métal
1) Champ créé par un plan uniformément chargé
On considère une surface plane de très
grandes dimensions, uniformément chargée, avec
la densité surfacique de charge 0, et un point M0
situé sur l’axe z’Oz normal à ce plan à la cote
z0 > 0. Le point O est sur la surface chargée.
a) En utilisant le théorème de Gauss et après
avoir précisé les symétries et invariances, exprimer
le champ électrostatique
0E
en M0 avec 0, 0 et le
vecteur unitaire
zu
de l’axe z’Oz.
b) En déduire le champ électrostatique
0'E
au
point M’0 de cote –z0 et la discontinuité du champ
0E
–
0'E
à la traversée de la surface chargée dans le sens de
zu
. On rappelle que ce dernier résultat reste
valable pour toute forme de la surface chargée et si la densité surfacique de charge n’est pas uniforme.
2) Champ créé par un conducteur en équilibre électrique
a) Un conducteur est en équilibre électrique si les charges qu’il contient ne sont soumises à aucune
force électrique.
Que peut-on en déduire pour le champ électrostatique à l’intérieur du conducteur en équilibre ?
Que peut-on en déduire pour le potentiel électrostatique à l’intérieur de ce conducteur ?
b) On considère un conducteur compris entre deux surfaces planes de grandes dimensions, de cotes 0 et
–H portant chacune une densité de charge 0.
Exprimer, avec 0 et
zu
, le champ électrostatique en un point M de cote z pour z > 0, puis pour
0 > z > –H, puis pour z < –H. Le conducteur est-il en équilibre électrique ?
c) Le conducteur est au potentiel électrostatique V1. Exprimer, avec V1, 0 et 0, en fonction de z, le
potentiel électrostatique en M pour z > 0, puis pour z < –H.
3) Influence d’une charge électrique ponctuelle sur la répartition de la charge d’un conducteur
Une charge ponctuelle q0 > 0
est maintenant placée en M0 de cote z0
> 0, au dessus du conducteur
précédent qui est maintenant relié à
une prise de terre (son potentiel est
V = 0). La hauteur H du conducteur,
comme ses autres dimensions sont
considérées comme infiniment
grandes par rapport à la distance z0.
Sous l’influence de la charge
q0, la surface  (z = 0) du conducteur
se charge électriquement. Il apparaît à
l’équilibre électrique une densité
surfacique de charge  non uniforme
sur la surface .
Un point quelconque sera repéré par ses coordonnées cylindriques r,  et z.
On note P un point de , repéré par r,  et z = 0, et P’ un point infiniment voisin de P, situé à
l’extérieur du conducteur, aux mêmes coordonnées r et  que P, mais à la cote z avec z << z0.
M0
O
z
z’
.
(0)
M0
O
z
z’
.
(0)
M0
z
z’
.O
conducteur
q0
M0
z
z’
.O
conducteur
q0

a) Quel est le signe de  ? D’où sont venues les charges accumulées sur  ?
b) Quel est le champ électrostatique à l’intérieur du conducteur en équilibre électrique ? Exprimer avec
, 0 et
zu
, le champ électrostatique total
E
au point P’ (on utilisera la discontinuité du champ).
c) Au point P’, le champ
E
peut être décomposé en
0
E
créé par la charge q0,
1
E
créé par un petit
disque, de rayon très grand devant z mais très petit devant z0, découpé sur  autour de P et
2
E
créé par le
reste de la surface .
Exprimer
0
E
avec q0, 0, M0P et
 PM0
, puis avec q0, 0, M0P, z0, r et les vecteurs unitaires
r
u
et
z
u
.
d) Exprimer
1
E
avec , 0 et
z
u
puis montrer que
2
E
est radial, c'est-à-dire de la forme
r
r22 uEE 
e) Déduire des résultats précédents l’expression de  avec q0, z0 et M0P, puis avec q0, z0 et l’angle 
formé par M0P et zOz’.
f) Calculer la charge électrique totale de la surface , (on utilisera la variable  pour faciliter
l'intégration).
4) Équivalence de la répartition de charge précédente avec un dipôle
Le champ créé par le plan chargé sous l'influence de la charge q0 est identique, au dessus du
conducteur, à celui que créerait une charge –q0 placée en M'0 symétrique de M0 par rapport à la surface .
On vérifiera ici quelques conséquences de cette identité aux questions b), c) et d) et on l'admettra pour la
suite.
a) Au point P' défini précédemment, exprimer le champ total
1
E
+
2
E
créé par la surface , avec q0, 0,
r, z0, ,
r
u
et
z
u
.
b) Exprimer le champ
0
'E
que créerait en ce même point P' la charge –q0 placée en M'0 et constater son
identité avec le résultat précédent.
c) Exprimer le champ
'E
créé par la surface chargée  au point M0 et constater son identité avec le
champ que créerait en M0 la charge –q0 placée en M'0.
d) Exprimer le potentiel électrostatique V' créé par la surface chargée en M0 et vérifier son identité avec
le potentiel que créerait en M0 la charge –q0 placée en M'0.
e) Exprimer avec q0, z0 et 0 l'énergie potentielle U0 d'interaction électrostatique entre la surface  et la
charge q0.
z
x
y
M0
r
P
P’
zu
ru
u
z
x
y
M0
r
P
P’
z
x
y
M0
r
P
P’
zu
ru
u

f) Exprimer le moment dipolaire
µ
de la distribution de charge formée par les charges ponctuelles q0
et –q0, avec z0, q0 et
z
u
.
g) En un point M situé loin au dessus de la
surface du conducteur, aux coordonnées sphériques r, 
et  (avec r >> z0), exprimer (sans démonstration), avec
q0, 0, r et , le potentiel électrostatique et en déduire les
coordonnées Er, E et E du champ créé par la charge
ponctuelle q0 et la surface chargée  du conducteur.
O
M0
M’0
M
x
y
z
r
φ
θ
O
M0
M’0
M
x
y
z
r
φ
θ