Chap 09

1. MODELISATION D’UNE ACTION MECANIQUE.
Lorsque Julie tire sur l’extrémité d’un élastique, elle exerce une action mécanique, modélisée par une force. Cette force est représentée par
un segment fléché (aussi appelé vecteur) auquel on peut attribuer:
Une action mécanique est toujours exercée par un objet (“l’acteur”) sur un autre objet
(“le receveur”).
On désigne la force ci-dessus par la notation FJulie/élastique
le doigt sur le
poussoir du stylo.
le pied sur la pédale
de frein.
soulever des haltères
de 100 kg.
un réacteur d’avion
sur les gaz qu’il éjecte.
un moteur de fusée
sur les gaz qu’il
éjecte.
1 N
102 N
103 N
105 N
ouvrir une porte de
placard à fermeture
magnétique.
10 N
traction d’une
caravane par une auto
(au démarrage).
104 N
traction d’un convoi
par une locomotive
(au démarrage).
106 N
force exercée par le
Soleil sur la Terre
107 N
3,5 x 1022
LA PHYSIQUE EXPLIQUE LA FORME DES PLANTES.
Les gènes ne font pas tout. Dans le monde végétal, ils ne puvent rendre compte seuls de la forme d’une feuille ou encore d’une fleur.
Un autre paramètre, capital, a été mis à jour: chaque cellule d’une plante est capable de sentir la force exercée par ses voisines lors de
sa croissance. Et, en plus, d’y résister. Cette résistance va rienter le «squelette» de la cellule et par la suite agir sur l’ensemble du
tissu. Les forces en présence vont donc diriger la croissance et seront responsables des formes variées que l’on connaît: feuilles
simples ou composées, palmées ou digitées, à bord uni ou dentelé ...
Les chercheurs ont suivi la dynamique des microtubes, ces protéines qui confèrent aux cellules leurs structure pendant la croissance
du tissu végétal. Ils ont d’abord modifié le champ de force local en enlevant une cellule et observé comment les cellules voisines se
réorganisent autour de la blessure. Ils ont également mesuré l’effet d’une pression extérieure. Conclusion: dans les deux cas, les
cellules s’alignent le long du champ de force apparu dans le milieu. Ces expériences ont été validées par des modèles empruntés à la
physique de la déformation des solides comme les ailes d’avions ou les bâtiments. Au final, la capacité individuelle à résister aux
forces suffit à créer une forme collective. La génétique n’est là que pour contrôler cette capacité à réagir ou bien pour accélérer ou
ralentir la croissance des cellules.
Il reste néammoins à comprendre comment ces dernières «perçoivent» les forces. Ensuite, il sera possible de créer des plantes
virtuelles, mêlant interactions génétiques et physiques, dont on pourra prévoir le développement et les formes en fonction de
différentes contrainte. SVJ - Fevrier 2009.
LES FORCES
une valeur:
qui dépend de la déformation du tendeur.
L’unité est le Newton (N).
La longueur du vecteur est proportionnelle à la valeur de la force.
un point d’application:
la petite surface de contact entre
sa main et le tendeur.
une direction:
celle de l’élastique
un sens:
de l’élastique
vers Julie
FJulie/élastique.

2. QUATRE FORCES FONDAMENTALES
Quatre, pas une de plus ! Cela suffit à la Nature pour faire le monde tel qu’il est. Certaines de ces forces - on emploie aussi le terme
“interactions” - vous sont familières alors que d’autres, au tréfonds des atomes, sont aussi discrètes qu’indispensables.
3. LES ACTIONS MECANIQUES ET LEURS EFFETS SUR LE MOUVEMENT.
Nous donnons le nom d’action mécanique aux actions exercées par un objet sur un autre.
Une action mécanique se manifeste sur les mouvements d’objets par ses effets que nous allons
maintenant décrire.
3.1. MODIFICATION DE LA VALEUR DE LA VITESSE.
Observation.
Un enfant pousse le chariot devant lui, immobile au départ. Il exerce une force sur le chariot orientée
vers l’avant. Le chariot se met en mouvement dans ce sens et la valeur de sa vitesse augmente.
Puis l’enfant retient le chariot pour freiner; il inverse ainsi le sens de la force qu’il exerce sur le
chariot. La valeur de la vitesse du chariot décroît jusqu’à l’arrêt.
Conclusion.
Une force appliquée à un corps peut modifier la valeur de sa vitesse.
3.2. MODIFICATION DE LA TRAJECTOIRE.
Dispositif.
On abandonne sans vitesse initiale une bille d’acier en haut d’un plan incliné.
Observation.
En l’absence de l’aimant, la trajectoire de la bille est une droite: le mouvement de la bille est rectiligne
En présence de l’aimant, la trajectoire de la bille s’incurve vers l’aimant: son mouvement n’est plus
rectiligne.
Interprétation.
L’aimant exerce sur la bille en acier une force appelée force magnétique. Cette force modifie la
direction du mouvement de la bille.
Conclusion.
Une force appliquée à un corps peut modifier la direction de son mouvement.

5. FORCE EXERCEE PAR LA TERRE SUR UN SOLIDE EN MOUVEMENT.
5.1. LA FORCE DE PESANTEUR.
Un objet qui se trouve au voisinage de la Terre subit une force gravitationnelle F qui peut s’identifier à la force de pesanteur P
le point d’application est appelé centre de gravité.
la direction est rigoureusement: suivant la droite qui relie les deux centres Gp et GT
en exercice: verticalement
le sens est rigoureusement: vers le centre de la Terre.
en exercice: vers le bas
l’intensité se nomme p et s’exprime en Newton (N).
p = m x g
avec g l’intensité de la pesanteur; elle s’exprime en N / Kg.
Cette constante varie selon l’endroit où on se trouve.
En France g est de l’ordre de 10 N / Kg.
Le poids, action répartie dans tout le volume d’un objet, peut être représenté par une force, notée p, dont:
L’attraction gravitationnelle de la Terre s’exerce sur chaque
particule d’un coprs placé en son voisinage. L’ensemble des
actions exercées par la Terre sur la pomme est équivalente à une
force unique.
5.2. LE CHAMP DE PESANTEUR EST UNIFORME.
La relation p = m x g est supposée vraie partout.
En réalité g dépend du lieu, m ne change pas. Donc p dépend du lieu. C’est la faible
variation de la valeur de g à la surface de la Terre qui crée la confusion entre masse et
poids.
Ainsi: - Il faut s’écarter de 111 km pour que l’angle de deux verticales atteigne un degré;
- D’autre part, il faut s’élever en altitude de 30 km pour que l’intensité de la
pesanteur diffère de 1% de sa valeur au sol.
Ainsi, nous pouvons considérer que dans un domaine où les dimensions n’excèdent
pas quelques kilomètres, le champ de pesanteur est identique en direction, sens et
intensité: on dit que le champ de pesanteur est uniforme. Dans une telle région le
vecteur champ de pesanteur g est constant.
Lorsque le champ de pesanteur est uniforme, son vecteur est porté par des verticales parallèles: ce sont des lignes du champ de pesanteur
qui sont orientées de haut en bas comme le vecteur champ de pesanteur g.
Remarque.
Ce champ existe en un point au voisinage de la Terre qu’il y ait ou non un objet de masse m placé en ce point au voisinage de la Terre. Cet
objet ne sert qu’à détecter le champ qui est crée par la Terre.
Gp
p TERRE/HOMME

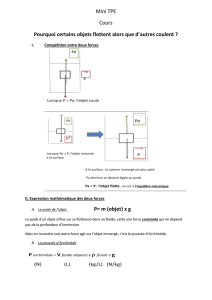
le point d’application est le centre de gravité Gf du fluide déplacé, appelé centre de poussée.
la direction est verticale
le sens est vers le haut.
l’intensité est égale à celle du poids du volume de fluide déplacé. On aura:
FArchimède = mfluide déplacé x g = fluide déplacé x Vfluide déplacé x g
Remarque.
La poussée d’Archimède n’est pas toujours prépondérante par rapport au poids du corps. Ainsi, malgré la
poussée d’Archimède, une bille d’acier coule dans l’eau. Seuls les corps dont la densité est inférieure à
celle de l’eau flottent sur l’eau.
Remarque.
L’air est également un fluide et exerce aussi une poussée d’Archimède sur tous les objets. Mais la poussée
d’Archimède dans l’air est 755 fois plus faible que la poussée d’Archimède dans l’eau. Elle passe donc inaperçue
et est ainsi souvent négligée dans de nombreux problèmes. Cependant, son rôle est essentiel pour les dirigeables
gonflés, gaz dont la densité est inférieure à celle de l’air.
La poussée d’Archimède peut être modélisée par un vecteur force:
6.1. LA POUSSEE D’ARCHIMEDE.
Problème à résoudre.
Dans l’eau, un objet nous paraît moins lourd que dans l’air. Une force se soustrait donc au poids de l’objet: on
l’appelle poussée d’Archimède.
Réponse.
C’est parce qu’une force, exercée par l’eau, vient s’opposer à l’action du poids de l’objet. Cette force est la
poussée d’Archimède. Elle se manifeste sur Terre sur tout objet immergé dans un milieu dit fluide comme l’eau.
C’est grâce à cette poussée qu’un bateau peut flotter par exemple.
On peut dire, dans un langage imagé, que la valeur de la poussée d’Archimède est égale au poids du fluide que
l’objet a remplacé lorsqu’il a été immergé. Elle dépend donc du lieu et de la masse du fluide remplacé par l’objet.
6. FORCES EXERCEES PAR UN FLUIDE SUR UN SOLIDE EN MOUVEMENT.
le point d’application la force s’exerce sur toute la surface du solide mais on se ramène au barycentre de la surface.
la direction est colinéaire au vecteur vitesse v du solide
le sens est dans le sens contraire du vecteur vitesse v du solide.
l’intensité
C’est l’action exercée par
l’air qui compense le poids et
permet au planeur de se
maintenir en vol.
portance
trainée
Fair
p
De façon générale, si un solide a un mouvement par rapport à un fluide, il subit une force de frottement f.
Dans le cas particulier d’un solide en chute verticale dans un fluide, la force de frottement f a les caractéristiques suivantes:
Le poisson, lorsqu’il est
immobile, n’est soumis qu’à
son poids et à la poussée
d’Archimède.
p
pA
La poussée d’Archimède a les mêmes caractéristiques si le solide est en mouvement ou immobile apr rapport au fluide.
Si le solide flotte sur un liquide, il subit la poussée d’Archimède exercée par le liquide et celle qui est exercée par l’air qui se trouve au-
dessus. Mais on néglige la poussée d’Archimède exercée par l’air par rapport à celle exercée par l’eau.
6.2. LA FORCE DE FROTTEMENT EXERCEE PAR LE FLUIDE.
Un skieur, une voiture en mouvement dans l’air, un nageur en mouvement dans l’eau subissent des actions mécaniques de contact qui ont
tendance à freiner leur mouvement. Ces actions mécaniques peuvent être modélisées par une seule force appelée force de frottement.
dépend de la vitesse du solide, de la nature du liquide, de la forme, des dimensions et de l’état de surface du solide.
On peut montrer que la valeur de la force de frottement est proportionnelle à vn; la valeur de n dépend de différents
paramètres, en particulier de la valeur de la vitesse.
Pour un solide en mouvement dans un liquide, dont la vitesse ne dépasse pas quelques cm.s-1, la valeur de la force de
frottement est de la forme f = k.v.
Dans le cas d’une sphère de rayon r tombant dans un fluide, le coefficient k est donné par la relation k = 6...r avec  la
viscosité du fluide.
Pour un solide en mouvement dans l’air dont la vitesse est de quelques m.s-1, la valeur de la force de frottement est de la
forme f = k’.v2. 1 0 la masse volumique du fluide
Le coefficient de frottement k s’écrit k = 0.Cx.S avecS l’aire de la grande section du solide au déplacement
2 Cx le coefficient de pénétration dans le fluide.

- il faut que la masse volumique du solide soit grande devant celle du fluide;
- il faut aussi que la vitesse du solide, sa forme, ses dimensions, sa surface soient telles que la force de frottement soit la plus faible
possible.
Remarque.
Dans le paragraphe 2, nous avons étudié la chute libre d’une balle dans l’air. Or l’air fait partie de la famille des fluides; il faudrait donc, en
toute rigueur, tenir compte des forces exercées par le fluide air sur la balle.
Bien que la chute s’effectue dans un fluide, on peut se rapprocher de cette situation idéale si les forces exercées par ce fluide sur le solide
(poussée d’Archimède et force de frottement) sont négligeables devant la force de pesanteur. Pour cela:
En pratique, ces conditions sont réalisées lorsqu’un solide dense et de forme aérodynamique chute dans l’air, sur une hauteur ne
dépassant pas quelques mètres.
Mais dans certains fluides, il n’est pas possible de faire abstraction de la poussée d’Archimède et des forces de frottement du fluide. C’est
l’objet de la suite du cours et du Tp  12.
LA POUSSEE D’ARCHIMEDE ET LES SABLES MOUVANTS.
Les sables
mouvants sont un
empilement
fragile de grains de
sable stabilisé par
des particules
d’argile.
Une légère pression
suffit à détruire
l’ensemble. Les grains
s’effondrent les uns sur
les autres. Les particules
d’argile se collent entre
elles et ne stabilisent
plus l’ensemble. L’eau
plus légère remonte.
Le mélange sable +
argile forme une
pâte très compacte
au fond, dont il est
quasiment
impossible de
s’extraire. L’eau
surnage. Le piège
s’est refermé sur le
personnage.
Une équipe de chercheurs hollandais vient de démontrer qu’on ne
peut pas être englouti par des sables mouvants. Ces fameux sables
sont un mélange de sable et d’argile gorgée d’eau. Les grains de
sable sont agglomérés par l’argile humide, qui agit comme un
ciment très léger. Cette argile forme une sorte de gel mi-solide mi-
liquide, qui a plus ou moins la consistance d’un yaourt.
De fait, un être humain qui pénètre dans la zone de sables
mouvants, ecerce une pression sur le sable. Cette force suffit à
briser l’empilement fragile des grains stabilisés par l’argile. Et tout
s’effondre comme un château de cartes. Au sein de l’argile,
plusieurs forces de nature électrique s’affrontent. Certaines sont
répulsives, d’autres attractives. Tant que personne n’a mis le pied
sur la sable, les forces répulsives l’emportent. Les sables
mouvants sont “aérés”: il existe beaucoup d’espace entre les
particules de sable. Mais la pression exercée par le pied chamboule
tout. Le fragile empilement est écrasé au sommet, et c’est une
réaction enchaîne qui s’amorce. Les forces attractives dansl’argile
l’emportent, les particules d’argile se collent entre elles et
n’assurent plus leur rôle de liant. Les grains, qui ne sont plus
tenus, s’effondrent étage après étage et se tassent au fond, tandis
que l’eau, plus légère que le sable et l’agile, surnage. L marcheur a
l’mpression que tout se liquéfie autour de lui. Et plus il bouge, plus
cela devient liquide. Il commence à s’enfoncer. Jusqu’aux genoux.
Jusqu’à la taille.
Et c’est tout ! Impossible qu’il soit totalement englouti. Il est
sauvé par la poussée d’Archimède. Tout corps plongé dans un fluide reçoit de sa part une poussée verticale, dirigée vers le haut, dont la
valeur est égale au poids du fluide déplacé. Ici, le fluide, c’est le mélange eau, argile et sable. Sa densité est deux fois plus élevée que
celle de notre corps. Autement dit, lorsque l’homme s’enfonce dans les sables mouvants, il subit une poussée vers le haut qui devient
égale à son poids. Et il flotte ! Cela se produit lorsqu’environ la moitié de notre corps, au pire les deux tiers selon la densité des sables, a
sombré.
Par contre, une fois prise au piège, il est extrêmement difficile d’en sortir seul. Un homme enfoncé jusqu’à la taille qui essaierait de lever
un pied devrait réaliser le même effort que pour soulever une voiture de une tonne ! Science & Vie Junior Décembre 2005.
POURQUOI LE BALLON DE RUGBY VOLE-T-IL PLUS LOIN QUE LE BALLON DE FOOT ?