4 Les forces

Chap 4  : LES FORCES 1ère S
I] Qu'est-ce qu'une force ?
1) Définition.
On appelle force, toute cause capable de modifier le mouvement d'un corps ou de le déformer.
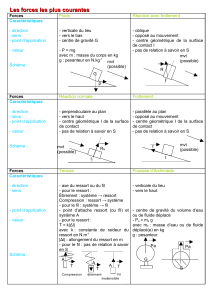
2) Caractéristiques et représentation d'une force.
Une force possède les caractéristiques suivantes :
 direction, sens, norme (valeur ou intensité) notée F ou F en newton N, point d'application.
On la représente graphiquement après avoir choisi une échelle de représentation.
3) Mesure de la valeur d'une force.
Un dynamomètre possède une partie déformable. La mesure de cette déformation  à l'action subie permet de connaître F.
4) Composition et décomposition des forces.
Le vecteur "somme des forces" est appelé résultante des forces
appliquées au système; il se construit souvent à partir d'un point
extérieur au système. Un vecteur force peut être remplacé par ses
composantes (souvent normale et tangentielle au plan du support).
II] Exemples de forces.
1) Force de gravitation et force de pesanteur.
Le poids P d'un corps de masse m donné par la formule P = m  g a comme caractéristiques :
Direction verticale, sens de haut en bas, intensité mg, point d'application G.
Cette force s'exerce à distance et résulte des forces de pesanteur s'exerçant sur tous les grains de matière du corps.
2) Poussée d'Archimède.
Un solide immergé dans un fluide homogène de masse volumique  est soumis à des actions
mécaniques de la part de ce fluide. Ces actions mécaniques sont modélisées par une force 
appelée poussée d'Archimède.
La poussée d'Archimède donnée par  =   V  g a comme caractéristiques :
Direction verticale, sens de bas en haut, valeur = au poids Vg du fluide déplacé ( en
kg.m-3, V en m3, g en N.kg-1), point d'application: le centre de gravité du fluide déplacé
appelé centre de poussée.
3) Réaction d'un support plan.
Le support exerce sur le solide des actions mécaniques qui peuvent être modélisées par une force
unique appelée réaction du support R et appliquée en I. Cette force a 2 composantes : l'une
normale au support (composante normale), l'autre dans le plan du support (composante
tangentielle). R = Rn + Rt. Rt  .Rn. S'il y a immobilité de l'objet par rapport au support.  est
le coefficient de frottement et dépend uniquement des surfaces en contact. Rq : si le solide est
en mouvement, la relation précédente devient Rt = .Rn.
4) Tension d'un fil ou câble.
Le remorqueur exerce sur le pétrolier une force T appelée tension du câble. La direction de cette force est confondue avec le câble.
5) Tension d'un ressort.
La force exercée par un ressort hélicoïdal à spires non jointives sur un objet qui lui est suspendu est appelée tension du ressort.
Elle a comme caractéristiques: direction = celle du ressort, sens opposé à la déformation du ressort, valeur k -0 avec k
la cte de raideur en N.m-1 et  allongement ou raccourcissement en m, point d'application = l'accroche du ressort et du corps.

6) Force de frottement fluide.
Un solide en mvt au sein d'un fluide est soumis de la part de celui-ci à une force de frottement qui a la même direction que celle du
vecteur vitesse mais de sens contraire. Elle est due à la viscosité du fluide et augmente lorsque la vitesse augmente.
III] Equilibre et mise en mouvement d'un solide.
On travaille dans le référentiel terrestre. Le principe d'inertie vu en seconde selon lequel un corps persévère dans son état de
repos ou de mvt rectiligne uniforme si les forces qui s'exercent sur lui se compensent va être ici précisé.
1) Equilibre d'un solide soumis à 2 forces.
Lorsqu'un solide soumis à 2 forces F1 et F2 est en équilibre :
 Les forces ont la même droite d'action.
 La somme vectorielle des 2 forces est nulle
0
21  FF
En fait, les forces F1 et F2 sont directement opposées.
2) Equilibre d'un solide soumis à 3 forces dont les directions ne sont pas //.
Lorsqu'un solide soumis à 3 forces F1, F2, F3 non // est en équilibre :
Les 3 forces sont concourantes,
La somme vectorielle des 3 forces est nulle
0
321  FFF
3) Mise en mouvement d'un solide.
Si les forces exercées à un solide ne respectent pas les conditions qui précèdent, elles seront suffisantes pour le mettre en mvt.
4) Cas particulier d'un solide mobile autour d'un axe fixe.
L'XP montre qu'une force dont la droite d'action coupe l'axe de rotation d'un solide
ou lui est // ne peut le mettre en rotation. Une force comme F3 qui possède une
composante  à son axe de rotation permet de le faire.