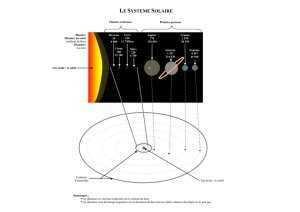
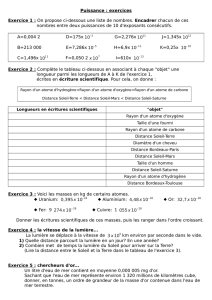
TP PHYSIQUE 1U : ETUDE DU SYSTEME SOLAIRE I

TP PHYSIQUE 1U : ETUDE DU SYSTEME SOLAIRE
I Objectif du TP
L’objectif de ce TP est de connaître les distances dans notre Système Solaire et la notion
d’année de lumière.
II Matériel
Ordinateur muni du logiciel Win Stars 2, tableur, règle graduée, calculatrice.
III Etude du Système Solaire: Existe-t-il une relation simple entre les distances entre
les planètes et le Soleil ?
Lancer le logiciel Win Stars 2.
Dans le menu Observation, sélectionner Voir le système solaire en entier.
Dans le menu Options, sélectionner configurations générales, Planètes et cocher l’affichage
des noms des planètes et des orbites.
A l’aide des outils de zoom et des flèches, zoomer et centrer la fenêtre sur le soleil afin de
visualiser l’orbite et les positions de Vénus, la Terre et Mars.
 Pour chacune des planètes, mesurer en cm la valeur sur l’écran du diamètre moyen de
l’orbite. En déduire la valeur sur l’écran de son rayon, lequel représente la valeur moyenne de
la distance entre le planète et le Soleil.
Vénus
La Terre
Mars
Diamètre
moyen
de
l’orbite (cm)
Rayon moyen de l’orbite
(cm)
Agir sur le zoom (-) pour faire apparaitre Jupiter. L’échelle ayant changé, déterminer de
nouveau (en cm) la valeur sur l’écran du rayon de l’orbite de Mars. Faire de même avec
Jupiter.
Mars
Jupiter
Diamètre moyen de
l’orbite (cm)
Rayon moyen de l’orbite
(cm)
Agir de nouveau sur le zoom (-) pour faire apparaitre Uranus. Effectuer la mesure à l’écran
du rayon de l’orbite de Jupiter, Saturne et Uranus.
Jupiter
Saturne
Uranus
Diamètre
moyen
de
l’orbite (cm)
Rayon moyen de l’orbite
(cm)
Agir une dernière fois sur le zoom (-) pour faire apparaitre Neptune. Terminer par la
mesure à l’écran de l’orbite d’Uranus et de Neptune.
Uranus
Neptune
Diamètre
moyen
de
l’orbite (cm)
Rayon moyen de l’orbite
(cm)
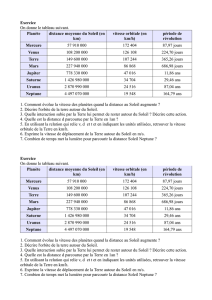
1- Calculer le rapport des distances au Soleil de Vénus et Mars sur la distance Soleil-Terre.
2- Calculer le rapport de la distance au Soleil de Jupiter sur la distance Soleil-Mars. En
déduire le rapport de la distance Soleil-Jupiter sur la distance Soleil-Terre.
3- Procéder de même pour déterminer le rapport des distances au Soleil de Saturne, Uranus
et enfin Neptune, sur la distance Soleil-Terre.
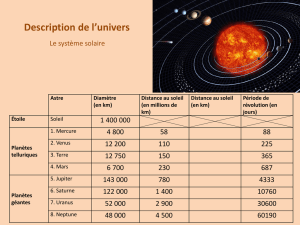
4- L’unité astronomique (notée u.a.) est égale à la distance Soleil-Terre. Construire un
tableau regroupant par ordre croissant, les distances en u.a. séparant le Soleil de chacune
des planètes du Système Solaire. La distance Soleil-Mercure est égale à 0,38 u.a.
5- En 1766, le mathématicien allemand J.Titius remarque de les distances D au Soleil des 6
planètes connues de l’époque (de Mercure à Saturne) semblent obéir à une règle
empirique, dite de Titius-Bode :
D = 0,40 + 0,30 N ; La valeur de D est exprimée en u.a. et les valeurs de N forment une
suite de nombres entiers : 0, 1, 21, 22, 23, 24, etc…
a.
A l’aide d’un tableur, calculer les valeurs de D prédites par cette règle jusqu’à N
= 27.
b.
Comparer qualitativement ces valeurs de D aux valeurs réelles des distances au
Soleil des 6 planètes. Associer alors une valeur de N à chacune d’elles.
c.
Des évènements assurèrent le succès de la règle de Titius-Bode : la découverte
de l’astéroïde Cérès en 1801, à la distance D = 2,77 u.a. et celle d’Uranus en 1781.
Expliquer.
d.
Indiquer pourquoi, après la découverte de Neptune, il n’était plus envisageable
de considérer la règle de Titius-Bode comme une loi de la physique.
e.
Est-il possible de déterminer les distances au Soleil de toutes les planètes grâce
à la loi de Titius-Bode ?